Одиннадцатая лекция

11. Законы распределения и проявление этих законов в теории надежности

План

Важность изучения распределений случайных величин в науке о надежности.

Дискретные распределения.

Непрерывные распределения: экспоненциальное и нормальное, а также распределения, занимающие промежуточное место между этими крайними случаями изменения интенсивности отказов.

Отказы – случайные события; время работы до отказа, число отказов на множестве изделий, время восстановления – случайные величины.

Для исчисления вероятностей должна быть информация. Ведь как можно исчислять то, о чем нет никаких сведений? Такую информацию дают законы распределения случайных величин: дискретные и непрерывные. Начнем с дискретных распределений.

11.1. Биномиальное распределение

Производится n независимых опытов, в каждом из которых некое событие А может появиться с вероятностью p и не появиться, следовательно, с вероятностью q = 1 – p [1].

Требуется найти вероятность P_m,n того, что событие А в этих опытах появится ровно m раз.

Для определения вероятности P_m,n подсчитаем число вариантов с появлением события А m раз в n опытах. Таких вариантов всего столько, сколько групп из n элементов по m, где порядок элементов не важен; то есть необходимо подсчитать число сочетаний из n элементов по m:

. (11.1)

Согласно теореме умножения вероятностей вероятность появления каждого из этих вариантов равна:

. (11.2)

С учетом того, что вероятность суммы несовместных событий равна сумме вероятностей этих событий, получаем искомую вероятность P_m,n к

, (11.3)

где С-число сочетаний из n элементов по m .

Применительно к области надежности технических средств формула (11.3) дает вероятность того, что из n элементов (образцов) откажут (n – m), а m останутся в работе, причем q - вероятность отказа элемента в каждом конкретном опыте.

11.2. Закон Пуассона

Этот закон выражает биномиальное распределение при большом числе опытов и малой вероятности появления события в каждом из них. Вот почему его называют законом редких явлений.

Положим, что в биномиальном распределении (11.3) число опытов стремится к бесконечности (n → ∞), а вероятность появления рассматриваемого события А – к нулю (р → 0); при этом произведение n·p имеет некое = a / n постоянное конечное значение (n·p = а), где - а параметр распределения.

При p = a / n

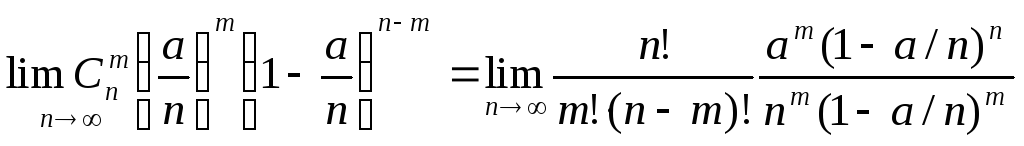. (11.4)

Анализ выражения при n → ∞ удобно провести, представив его в виде

. (11.5)

Отсюда, с учетом правомерной аппроксимации получается окончательно

. (11.6)

Если приложить анализируемое распределение к потоку случайных событий, вероятность есть вероятность попадания события на m временных отрезков из общего их числа n при n → ∞.

Пример. В оборудовании 1 раз за 50 суток работы обнаруживается неисправность, приводящая к отказу. Найти вероятность появления от 2-х до 4-х отказов за 5 суток (то есть за рабочую неделю).

Из условий задачи вытекает, что p = 0,02 отказа / сутки. Т. к. n = 5, параметр распределения Пуассона равен а = n·p = 5· 0,02 = 0,1.

Подсчитаем вероятность P = P₂ + P₃ + P₄ , откуда

P = 0,0045 + 0,0002 + б.м. = 0,0047.

Другой пример. В системе связи с протоколом произвольного доступа поток событий передачи пакетов информации (вместе с повторной передачей) представляет пуассоновский процесс. Определить вероятность возникновения конфликта с еще одним пользователем, если среднее значение полной частоты передачи пакетов составляет при средней длительности пакета Δt_п = 10 мс.

Среднее число сообщений, приходящееся на временной отрезок τ , определяется как (λ · τ). Параметр распределения Пуассона в данном случае находится как .

Сам закон Пуассона может быть записан здесь следующим образом:

_. (11.7)

причем в нашем случае m = 1.

Искомая вероятность составит: Р = 0,1·е ^{– 0,1} = 0,09.

Если число отказов, попадающих на интервал времени τ, распределено по закону Пуассона (11.7), параметр λ представляет среднее число отказов в единицу времени.

Теперь – о непрерывных распределениях.