Вторая лекция

Часть 1. Взаимозаменяемость

План лекции

Преамбула: Общая идея взаимозаменяемости ее изложение применительно к взаимозаменяемости по геометрическим параметрам. Размер и точность размера как ключевые понятия взаимозаменяемости; особенности геометрических размеров элементов.

Номинальный размер. Ряды предпочтительных чисел. Действительный и предельный размеры. Допуск, поле допуска.

Для любого изделия существен некоторый набор своих параметров, каждый из которых в физико-техническом смысле есть величина, характеризующая определенные свойства конструкции, материала, процесса…

Например, для электродвигателя можно назвать его конструктивные параметры (габаритные и присоединительные размеры), электрические (питающие/управляющие напряжения, токи, потребляемая мощность), механические (момент на валу, скорость вращения…).

По отношению к любой физической величине (ФВ) применяется понятие «размер».

Размер – это количественная определенность ФВ, присущая конкретному объекту. Еще определенность ФВ выражается ее значением, то есть оценкой размера в виде некоторого числа единиц измерения. Числовое значение ФВ изменяется в зависимости от размера единицы измерения:

14 унций = 396,9 г;

1 см = 10 мм = 10⁴ мкм ≈ 0,3937 дюйма.

При этом сам размер ФВ ни от каких единиц измерения не зависит (то есть размер инвариантен к выбору единиц измерения).

В этом первом разделе курса главное внимание уделяется взаимозаменяемости (В) по геометрическим параметрам, то есть – по линейным и угловым размерам элементов деталей. Подчеркнем, что речь – о точности именно элементов деталей.

Почему наибольшее внимание будет уделено геометрическим размерам, а не размерам ФВ вообще? Дело в том, что длина, диаметр, толщина и прочие геометрические размеры неоднозначнее и труднее определяемы, нежели размеры практически любых других ФВ (примеры с измерением веса тела на определенной широте и высоте места, силы электрического тока и др.).

Следует еще заметить, что измерения линейных размеров составляют в машиностроении и приборостроении от 80 до 90% всех технических измерений, проводимых в этих отраслях.

1. Размеры и их точность.

1. Номинальный, действительный и предельный размеры.

Характеризуемый словом «номинальный» обычно является каким-либо только по названию; сам термин происходит от латинского nominalis (именной). Значение этого слова применительно к размерам элементов деталей, сопряжений таково: на чертежах (деталей, сборочных единиц) проставляют номинальные размеры, которые не обязательно являются желаемыми. Применительно к сопряжению – на сборочном чертеже – проставляется один общий для деталей данного сопряжения номинальный размер.

Номинальный размер, проставляемый на чертеже, служит началом отсчета отклонений; указываемые после числового значения номинального размера два предельных отклонения, по сути, задают два предельно допустимых значения размера.

Номинальный размер определяется из расчетов или выбирается из конструктивных соображений и округляется до ближайшего большего размера из ряда нормальных линейных размеров.

В разных областях естествознания и техники встречаются (и вводятся) последовательности упорядоченных величин. Прежде всего здесь имеются в виду ряды предпочтительных чисел .

Принято считать, что систему предпочтительных чисел изобрел в 1886 г французский инженер-капитан Шарль Ренар, предложивший для градации диаметров канатов геометрические прогрессии. В честь изобретателя обозначения рядов предпочтительных чисел содержат букву R. Знаменатели геометрических прогрессий обозначаются буквой Q.

Образованные таким образом ряды R5; R10; R20; R40 называются основными; ряды R80; R160 – дополнительными (табл. 1); число после буквы R указывает количество чисел в десятичном интервале. Предпочтительны ряды с более крупной градацией размеров (с большим знаменателем прогрессии).

Таблица 1

Ряды	R	Q
Основной	5
» »	10
» »	20
» »	40
Дополнительный	80
» »	160

Наиболее предпочтительный ряд R5 нашел выражение в построении «Единой системы допусков и посадок», в частности, в установлении границ интервалов линейных размеров, выборе последовательности значений допусков по квалитетам. Подробнее эти вопросы будут рассматриваться в соответствующем разделе.

Интересно проследить историю возникновения введенных более 100 лет назад Ренаром рядов. Скрыта ли в структуре этих рядов еще какая-либо закономерность, кроме той, которая присуща членам геометрической прогрессии?

Здесь уместно вспомнить некоторые исторические сведения.

В древние века было установлено «золотое» деление («золотое» сечение) [1] отрезка:

или , (1.1)

где L – длина всего отрезка; a – большая его часть; b – оставшаяся часть отрезка.

Отношение L / a = x нетрудно определить из уравнения

x² – x – 1 = 0, (1.2) что дает x = ≈ 1,62.

Фронтинус (автор книги, написанной в 97 г. до н. э.) привел значения диаметров колес древнеримских акведуков; градация этих диаметров подчинялась геометрической прогрессии. Известно также [2], что зодчие Византии, Эллады, Киевской Руси при определении соотношения размеров своих сооружений пользовались геометрической прогрессией со знаменателем Q = 1,62.

Геометрическую прогрессию образуют также частоты тонов музыкальной шкалы [3]. Если число ступенек между частотами f ₀ и 2f ₀ (октава) обозначить m, то знаменателем прогрессии является число Q = . А для исчисления размеров мы пользуемся десятичной системой и, соответственно, Q = .

Рис. 1.1

На интересные свойства рядов предпочтительных чисел указано в работе [2] (например, свойство равенства крайних и средних сумм). Там же приведены впечатляющие примеры из естествознания, подтверждающие связь этих чисел с упорядоченными последовательностями некоторых наблюдаемых в природе величин. Все сказанное позволяет сделать вывод: ряды предпочтительных чисел отражают глубокие закономерности, присущие явлениям природы.

Итак, нормальные линейные размеры в диапазоне 0,001 до 20000 мм построены на основании рядов предпочтительных чисел (рядов Ренара), являющихся геометрическими прогрессиями со знаменателями Q = (см. табл. 1). Число в обозначении ряда указывает количество членов прогрессии в десятичном интервале.

В отдельных случаях требуются округления чисел из приведенных выше рядов. Так появились ряды первого и второго округлений R^/ и R^//. Например, числа 1,5 и 6,0 из ряда R^//5 используют вместо соответствующих им чисел 1,6 и 6,3 ряда R5.

Действительный размер физической величины (ФВ) – тот, который установлен измерением с допустимой погрешностью. [Значение истинного размера не известно, хотя он существует].

Когда мы измеряем величину емкости конденсатора или, например, величину напряжения на клеммах электрической батареи с помощью соответствующего цифрового прибора, то просто считываем с его табло высвечиваемые показания. Аналогично происходит измерение веса, частоты импульсов, да и большинства других ФВ.

Для линейного размера (длины, диаметра, высоты и др.) определение его действительного значения сложнее, чем для других величин. Дело в том, что элементы деталей – объемные тела, форма которых неидеальна. Это можно проиллюстрировать на следующем рис. 2. Какой из указанных размеров можно считать действительной длиной показанного здесь бруска?

Такая же неоднозначность проявляется и в определении диаметра вала, казалось бы круглого, но в действительности неправильной формы (рис. 3).

Рис. 1.2

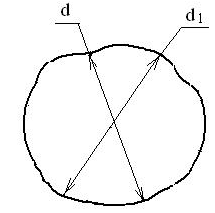
Рис. 1.3

В определении действительного размера элемента детали внимание обращено к соединению двух элементов: охватываемого (условно «вала») и охватывающего («отверстия»), то есть в даваемом далее определении «заложена» идея действующего в сопряжении размера [4] рассматриваемого элемента.

Действительным размером отверстия или вала считается размер сопрягаемой детали идеальной геометрической формы, прилегающей к поверхности рассматриваемого элемента без зазора.

Хотя идея определения действительного размера элемента по прилегающему цилиндру в принципе верна (именно этот размер будет «участвовать» в образовании посадок), на практике реализовать ее (данную идею) трудно: нет надежного и простого способа измерения размера идеального прилегающего элемента [4].

Все действительные размеры должны быть ограничены предельными размерами.

В принципе, вся проблема нормирования точности любых размеров заключается в необходимости указать изготовителю (а затем и контролеру) два предельно допустимых значения размера (ФВ, элемента детали), при выходе за которые изделие становится негодным:

D_min ≤ D_д ≤ D_max ;

C_min ≤ C_д ≤ C_max …

На практике было бы очень неудобно при оформлении чертежей пользоваться непосредственно значениями предельных размеров. Для упрощения чертежей введены предельные отклонения от номинального размера: верхнее (error super) и нижнее (error inner), обозначаемые ES, es и EI, ei для отверстия и вала соответственно.

Эти отклонения определяются по формулам:

ES = D_max – D; es = d_max – d; (1.3)

EI = D_min – D; ei = d_min – d. (1.4)

Таким же образом вводится действительное отклонение:

E_д = D_д – D; e_д = d_д – d. (1.5)