УМК ВиН correp / КЛ / Лекция 12

Двенадцатая лекция

12. Потоки отказов/восстановлений

План

Поток событий как вероятностный процесс. Моденль потока отказов/ восстановлений в сложной технической системе.

Вывод уравнений Колмогорова-Чепмена применительно к системе с двумя состояниями.

Функция готовностти.

Анализ вероятностного процесса в системе с резервированпием с тремя состояниями.

Здесь, прежде всего, следует охарактеризовать поток смены состояний объекта как вероятностный процесс. В дальнейшем будем полагать, что термины “поток событий” и “процесс” означают одно и то же.

Наиболее подходящим для описания процессов в сложных технических системах является марковский процесс [1]. Особенность его – в том, что для каждого момента времени вероятность любого состояния объекта в будущем зависит только от состояния объекта в настоящий момент и не зависит от того, каким образом объект пришел в это состояние.

Рассмотрим вероятностный процесс попеременного нахождения технической системы в одном из двух состояний: работоспособности (состояние S1) и ремонта (состояние S2). Предположим, что поток отказов в данной системе – пуассоновский, с интенсивностью отказов λ; предположим также, что время восстановления системы после очередного отказа – случайная величина, распределенная по экспоненциальному закону. Здесь следует подчеркнуть, что экспоненциальность распределений времени работы до отказа и времени восстановления – существенные условия, без которых процесс не был бы марковским [1, 2, 3].

Обозначим вероятности нахождения системы в указанных состояниях (S₁ и S₂) P₁(t) и P₂(t) соответственно. Очевидно, что P₁(t) + P₂(t) = 1.

Рассмотрим поведение системы в интервале времени [t, t+Δt] и найдем вероятность нахождения системы в момент t+Δt в состоянии работы.

Эта вероятность может быть записана как

, (12.1)

что означает: из рабочего исходного состояния S₁ система не перейдет в состояние S₂ с вероятностью , а из состояния ремонта она вернется в рабочее состояние S₁ с вероятностью (1 - ).

При λ∆t << 1, μ∆t << 1 (это имеет место, если длительность интервала ∆t много меньше среднего времени наработки до отказа) допустима следующая аппроксимация:

≈ 1 - λ∙∆t, 1 - ≈ μ∙∆t. (12.2)

Тогда (12.1) записывается в виде

. (12.3)

Аналогичные рассуждения приводят к выражению

. (12.4)

Далее очевиден переход к дифференциальным уравнениям при ∆t→0:

(12.5)

.

Дифференциальные уравнения (12.5) получили название уравнений Колмогорова-Чепмена.

Решить эти уравнения можно, например, обратившись к преобразованиям Лапласа

P

(12.6)

_i(t) → P_i(s); i = 1,2;

→ s · P_i(s) – P_i(0),

и тогда дифференциальные уравнения переходят в алгебраические:

sP₁(s) - P₁(0) + (λ + μ) P₁(s) = μ . (12.7)

Остается в конечном итоге найти P₁(t):

(12.8)

При ∆t → ∞ получается стационарное решение

. (12.9)

Рассматриваемый вероятностный процесс удобно представлять графом состояний с указанием на ребрах графа интенсивностей переходов из одного состояния в другое:

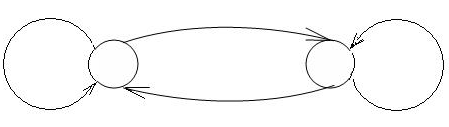
Рис. 12.1. Граф состояний системы с двумя возможными состояниями

Применим рассмотренный выше подход для исследования системы с резервированием (рис. 12.2), которая может находиться в трех состояниях [4]:

Р иc. 12.2. Модель надежности системы с резервированием

• оба дублирующих друг друга элемента системы работоспособны;

• один из элементов (образцов) находится в ремонте;

• оба образца отказали и восстанавливаются.

Обозначим указанные состояния соответственно S₀, S₁, S₂..

Вероятность того, что система на интервале Δt , применительно к моменту t₁, будет в состоянии S₀ будет такова:

(12.10)

Здесь допустимы следующие аппроксимации:

;

()() = б.м..

Из уравнения (12.10) следует дифференциальное уравнение:

(12.11)

Г

1- 2μΔt

раф состояний рассматриваемой системы с резервированием показан на рис. 12.3.

1- 2λΔt

2 λΔt

μΔt

λΔt

2μΔt

Рис. 12.3. Граф состояний системы и двух параллельно работающих образцов

Рассуждая аналогично (с привлечением теорем умножения и сложения вероятностей), запишем вероятность того, что система в момент (t+Δt) , будет в состоянии S₁:

(12.12)

Здесь первое слагаемое – вероятность того, что элемент, находящийся в состоянии ремонта, продолжает в нем находиться, а другой элемент за это время не отказывает;

второе слагаемое - вероятность того, что один элемент из работоспособного состояния перешел в неработоспособное, причем это получилось из состояния “0”;

третье слагаемое - вероятность того, что из состояния “2” какой-либо элемент восстановится за время Δt. Из уравнения (12.12) получится следующее дифференциальное уравнение:

(12.13)

Наконец, рассмотрим вероятность перехода системы в состояние “2”:

; (12.14)

(следует отметить, что

, (12.15)

т.е.

(12.16)

Выпишем полную систему трех полученных дифференциальных уравнений:

:

(12.17)

Снова попробуем применить теорему Лапласа:

. (12.18)

Будем считать, что при t=0 P₀ =1; P₁ =0; P₂ =0.

; (12.19)

Введем функции готовности

А(t) = P₀(t) + P₁(t) . (12.20)

Находя P(s) и используя обратные преобразования Лапласа, получим

Вернемся к дифференциальным уравнениям (3.17): для установившегося режима (процесса при t → ∞ )

. (12.21)

Тогда

(12.22)

;

;

Обязательно надо учесть, что

(12.23)

Для получения окончательного результата остается сделать ряд формальных преобразований:

(12.24)

В итоге:

(12.25)

Литература

1. Острейковский В.А. Теория надежности: Учебник для вузов. М.: - Высш. шк., 2008. - 463 с.

2. Голинкевич Т.А. Прикладная теория надежности. – М.: Высш. шк., 1985.- 168 с.

3. Черкесов Г.Н. Надежность аппаратно-программных комплексов. – СПб.: Питер, 2005. – 479 с.

4. Александровская Л.Н., Афнасьев А.А., Лисов А.А. Современные методы обеспечения безотказности сложных технических систем: Учебник. – М.: Логос, 2003. - 208 с.