УМК ВиН correp / КЛ / Лекция 6. Расчет размерных цепей

Шестая лекция

5. Размерные цепи

План

Общие сведения о размерных цепях.

Виды размерных цепей

Задачи расчета размерных цепей

Численный пример проектного расчета размерной цепи

Взаимозаменяемость определяется не только точностью попарных соединений, но часто – суммарной точностью комплекса элементов конструкции (машины, прибора).

Размерная цепь (РЦ) – совокупность размеров, относящихся к изделию, непосредственно участвующих в решении поставленной задачи (конструкторской, технологической, измерительной) и образующих замкнутый контур (цепь). Каждый размер – звено такой цепи.

В любой РЦ всегда есть одно звено, называемое замыкающим, которое физически получается последним (при изготовлении, сборке или при измерении). При постановке задачи расчета РЦ это звено – исходное.

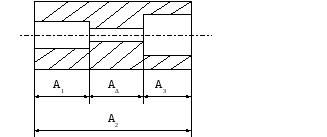
Рис. 5.1. Схема измерительной размерной цепи

Так, для случая измерения размера А_Δ показанной на рис. 5.1 детали этот размер и является замыкающим звеном, поскольку его можно определить только после измерения других размеров образуемой здесь цепи – замкнутого контура размеров А₁ - А_Δ - А₃ - А₂ - А₁.

Схема конструкции, иллюстрирующей сборочную РЦ, приведена на рис. 5.2. Основу этой конструкции представляет корпус 1. В нем установлены два центрирующих узла (2 и 2'), которые обеспечивают центрированное положение относительно них чувствительного элемента 3 инерциального прибора (система поддержания его положения соосно с узлами 2 и 2' не рассматривается). Замыкающим звеном в соответствующей размерной цепи (рис. 5.3) является суммарный зазор (А_Δ' + А_Δ'').

Рис. 5.2. Схема конструкции макета системы осевого магнитного центрирования поплавкового чувствительного элемента: 1 – корпус; 2, 2^/ - центрирующие узлы; 3 – центрируемый элемент.

Рис. 5.3. Схема размерной цепи конструкции макета системы осевого центрирования

Остальные размеры РЦ – составляющие. Все они по отношению к замыкающему (исходному) звену делятся на увеличивающие и уменьшающие размеры (звенья), в зависимости от того, увеличивается или уменьшается замыкающий размер при увеличении рассматриваемого составляющего звена.

Самый элементарный частный случай РЦ – соединение вала и отверстия (рассмотрим для положительного зазора):

Рис. 1.5.4. Представление посадки как частного случая РЦ: А₁ – размер отверстия, А₂ – размер вала, А₀ – зазор (замыкающее звено); а) схемы конструкций; б) схема РЦ

Размерную цепь (РЦ) называют линейной, если ее звеньями являются линейные размеры. Размерные цепи, звеньями которых являются, угловые размеры, называются угловыми размерными цепями. Размерная цепь называется плоской, если все звенья ее лежат в одной или нескольких параллельных плоскостях. Пространственной называют размерную цепь, все или часть звеньев которой расположены в непараллельных плоскостях.

Наиболее простыми являются одномерные (коллинеарные) линейные РЦ (рис. 5.1, 5.3, 5.4,б). Если звенья РЦ не расположены параллельно, то A_j берется как проекция соответствующего вектора на линию замыкающего размера.

Задачи расчета размерных цепей

Эксплуатационные свойства машин, приборов и многих других изделий зависят в основном от замыкающего звена РЦ. Именно для замыкающего звена при разработке конструкции должен быть установлен интервал (А_Δэ,нм, А_{Δэ, нб}) эксплуатационных допустимых значений. Точность составляющих звеньев РЦ играет подчиненную роль: интервалы допустимых значений этих размеров должны устанавливаться исходя из заданного интервала (А_Δэ,нм, А_{Δэ, нб}) . Совершенно обоснованно замыкающее звено именуется также исходным.

Основная задача, решаемая на этапе проектирования (задача проектного расчета РЦ): определить интервалы допустимых значений размеров составляющих звеньев по заданному интервалу (А_Δэ,нм, А_{Δэ, нб}) эксплуатационно допустимых значений замыкающего звена. Данная задача (еще называемая задачей синтеза) может быть сформулирована и в отношении предельных отклонений.

Если предельные отклонения составляющих размеров известны (в результате решения проектной задачи), то для проверки их соответствия интервалу (А_Δэ,нм, А_{Δэ, нб}) решают обратную задачу.

Расчетные соотношения, необходимые для решения задач РЦ

Отправное соотношение, связывающее параллельно расположенные звенья:

, (5.1)

где m – число увеличивающих размеров; p - общее число звеньев (вместе с исходным).

Из (5.1) следуют выражения для наибольшего и наименьшего значений А_Δ :

; (5.2)

. (5.3)

Отсюда, на основании определения допуска Т размера А как

T = A_нб – A_нм (5.4)

легко получить формулу, связывающую допуски всех звеньев:

. (5.5)

То есть допуск замыкающего звена равен сумме допусков составляющих звеньев, что имеет совершенно очевидный смысл: нельзя получить высокую суммарную точность изготовления, сборки, измерения без соответственно высокой точности элементов, из которых складывается результат указанных процессов.

Для решения задач РЦ необходимо располагать еще и соотношениями, связывающими предельные отклонения звеньев. Они также могут выведены из отправных выражений (5.2), (5.3) с учетом того, что

A_jнб = A_j + E_s(A_j);       A_jнм = A_j + E_i(A_j),       (5.6)

где E_S, E_i – верхнее и нижнее предельные отклонения.

Тогда

; (5.7)

. (5.8)

Теперь можно решать задачи расчета РЦ. Следует особо подчеркнуть, что полученные выше формулы применяют для решения задач при условии полной взаимозаменяемости (метод максимума-минимума).

Способы решения задачи проектного расчета РЦ

Здесь необходимо, во-первых, распределить допуск замыкающего звена по составляющим звеньям, а, во-вторых, назначить предельные отклонения. Первая часть задачи может быть выполнена двумя способами:

- равных допусков;

- равноточных допусков.

Более простой, но, вместе с тем, грубый – способ равных допусков:

T_j = T_ср = T_Δ / (p-1), (5.9)

Полученное значение следует округлить до стандартного(ых), после чего проверить выполнение условия

. . (5.10)

Этот способ дает хорошие результаты только для РЦ с близкими по величине составляющими звеньями. Если же составляющие размеры цепи существенно отличаются по величине, то будут сильно различаться и квалитеты их точности. Например, допуск IT = 25 мкм соответствует 9-му квалитету для размера 3 мм и 5-му квалитету для размера 400 мм. Такое различие квалитетов точности неэкономично (ведь, как уже отмечалось, каждый более точный квалитет дается при нелинейно возрастающей стоимости).

При решении задачи способом равноточных допусков стремятся получить допуски составляющих размеров по одинаковым квалитетам. Следовательно, в допуске каждого звена должно содержаться одно и то же число n единиц допуска.

Здесь исходят, таким образом, из формулы

IT_j = n_ср * i_j(A) ,       (5.11)

где i_j(A) – единица допуска размера А.

Отсюда искомое число единиц допуска находится как

. (5.12)

Полученное значение n_ср дает возможность выбрать №№ квалитетов так, чтобы выполнялось условие (5.10).

После того, как допуски назначены, остается найти предельные отклонения. Сделать это удобнее всего, следуя известному правилу [1, 2, 3]: полем допуска каждого из размеров охватывающих внутренних элементов считать поле допуска основного отверстия (рис.5.5,а), полем допуска каждого из размеров охватываемых наружных элементов считать поле допуска основного вала (рис. 5.5,б), а поля допусков звеньев, не относящихся ни к валам ни к отверстиям считать симметричными относительно линии номинального размера (рис. 5.5,в). Это правило надо применить ко всем составляющим размерам, за исключением одного – увязочного или резервного. Два предельных отклонения этого резервного звена остаются неизвестными, определяемыми из двух уравнений.

Рис. 5.5. К выбору предельных отклонений составляющих звеньев размерной цепи (проектный расчет)

Далее предлагается численный пример проектного расчета РЦ.

Дано. Размерная цепь (рис. 5.3), относящаяся к конструкции, приведенной на рис. 1.5.2. Величина магнитного зазора А_Δ задана в следующем эксплуатационном интервале: 40 ≤ А_Δ ≤ 150 мкм. Номинальные размеры:

А₁ =А3 = 10 мм; А₂ = 80 мм; А₄ = 60 мм.

Требуется определить предельные отклонения E_i(A_j) - ?, E_s(A_j) - ?

Решение. Число единиц допуска n_cр рассчитывается по формуле (5.12) при следующих значениях единиц допуска i_j:

i₁ = i₃ = 0,9 мкм; i₂ = i₄ =1,9 мкм.

n_cр = 110 / 5,6 = 19,6 .

Полученное число, дает основания взять допуски по квалитетам 7 и 8. Пусть IT₁ = IT₃ = 22 мкм (8-й кв.); IT₂ = IT₄ = 30 мкм (7-й кв.)

Σ IT_j = 104 мкм, что меньше ширины заданного эксплуатационного интервала примерно на 6%.

Теперь надо определить границы полей допусков E_i(A_j) - ?, E_s(A_j) - ?

Увязочным (резервным) звеном назначим А₂ (расстояние между торцевыми поверхностями корпуса). Для размера А₄ примем поле допуска основного вала (рис. 5.5), а для размеров А₁, А₃ – симметричные относительно линии номинального размера поля допусков.

Уравнения (5.7), (5.8) в рассматриваемом случае имеют вид:

E_SΔ = E_S2 – E_i1 - E_i3 - E_i4 ;

E_iΔ = E_i2 – E_S1 – E_S3 – E_S4 .

Из этих уравнений и определяются неизвестные E_S2 и E_i2 :

E_s2 = 150 – 22 – 30 = 98 мкм; E_i2 = 40 + 22 + 0 = 62 мкм.

Допуск Т = 36 мкм округлим до стандартного IT = 30 мкм.

Литература

1. Белкин В.М. Допуски и посадки (Основные нормы взаимозаменяемости). – М.: Машиностроение, 1992.- 528 с.

2. Дунин-Барковский И.В. Взаимозаменяемость, стандартизация и технические измерения. – М.: Издательство стандартов, 1987. - 352 с.

3. Якушев А.И. Взаимозаменяемость, стандартизация и технические измерения. – М.: Машиностроение,1986.