Преобразование фурье Прямое и обратное преобразование Фурье

Совокупность операций, позволяющих по заданной функции f(t) находить соответствующую ей спектральную характеристику F(iω) называется преобразованием Фурье:

Символически формулу (1)будем записывать в виде

Интеграл в правой части (1) как и ранее понимается в смысле главного значения, т.е.

Равенство (1) устанавливает связь между функцией f(t), аргументом которой служит t, и ей соответствующей комплексной функцией F(iω), имеющей в качестве аргумента частоту ω .

Формула интеграла Фурье

позволяет от известной функции F(iω) определить соответствующую ей функцию f(t). На этом основании формулу (3) называют обратным преобразованием Фурье. Символически будем записывать

В ряде задач автоматического регулирования функция f(t) характеризует процесс, имеющий место лишь начиная с некоторого момента времени t , который можно принять за нулевой.

В этом случае f(t) ≡0 при t< 0 (1) принимает вид

Преобразование (5) называется прямым односторонним преобразованием Фурье .Обратное преобразование Фурье, соответствующее прямому одностороннему преобразованию, остается двусторонним по переменной ω и дается равенством

При t=0, значение правой части (6) равно ;

при t < 0 , f(t) ≡0

Связь преобразований фурье и лапласа Формула

прямого преобразования Лапласа может рассматриваться как результат определенным образом построенного обобщения одностороннего преобразования Фурье.

Пусть, например, f(t) удовлетворяет условиям Дирихле в интервале 0 ≤ t < ∞ , причем f(t) ≡0 при t<0.

Как известно, преобразование Фурье может быть применено к функциям f(t), для которых интеграл существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе процессов в автоматических системах, например 1(t), Asin(ωt), Acos(ωt), e^αt при α >0, t и др.

Для того чтобы иметь возможность подобную функцию f(t) преобразовать по Фурье, предварительно ее надо умножить на e^-ct где вещественное число С>C₀ выбрано таким образом, чтобы интеграл был бы сходящимся.

Значение С₀ для каждой функции f(t) является вполне определенным. Используя формулу прямого одностороннего преобразования Фурье, будем преобразовывать по Фурье не f(t) , а f(t)e^-ct, удовлетворяющую условиям применения этого преобразования.

Введя новую комплексную переменную S=c+jω, получим .

Это выражение представляет собой формулу прямого преобразования Лапласа. Таким образом, преобразование Лапласа является результатом распространения преобразования Фурье на функции, которые, удовлетворяя условиям Дирехле в интервале 0<t< ∞, не удовлетворяют в этом интервале условию абсолютной интегрируемости.

Если F(jω) спектральная х – тика f(t), то функция F(S) комплексной переменой S является спектральной характеристикой затухающей функции времени f(t)e^-ct.

Рассмотрим формулу обратного преобразования Фурье:

Заменим в правой и левой частях этого равенства f(t) на f(t)e^-ct, получим:

Учитывая, что S=e + jω, dω=dS/j, найдём

Это равенство является формулой обратного преобразования Лапласа, т.е. обратное преобразование Лапласа может рассматриваться как развитие обратного преобразования Фурье.

Ранее отмечалось, что представление функции в виде интеграла Фурье соответствует представлению функции в виде суммы бесконечно большого числа гармоник с бесконечно малыми амплитудами, причем частоты гармоник отличаются друг от друга бесконечно мало. Аналогично этому представлению f(t) в виде (*) соответствует представлению этой функции в виде бесконечно большого числа бесконечно малых составляющих, являющихся колебаниями с бесконечно малыми амплитудами, затухающих по экспоненциальному закону.

Свойства преобразования Фурье аналогичны свойствам преобразования Лапласа.

Спектральные характеристики некоторых функций

1.Единичная ступенчатая функция. Дельта – функция.

Функция 1(t) вида

называется единичной ступенчатой функцией. Из (1) следует, 1(t) при t=0 имеет разрыв неопределенности первого рода, причем значение функции в точке разрыва не определено. Однако 1(t) при t=0 приписывают вполне определённые значения. Наиболее часто встречаются функции следующего вида:

Выбор того или иного значения единичной функции t=0 связан особенностями решаемой задачи. Например, первое представление удобно в том случае, когда рассматривают функцию 1(t) как предел при λ→∞ последовательности непрерывных функций:

f(t,λ)=1/2+(1/π)arctg λt (3) ,

где λ – параметр и

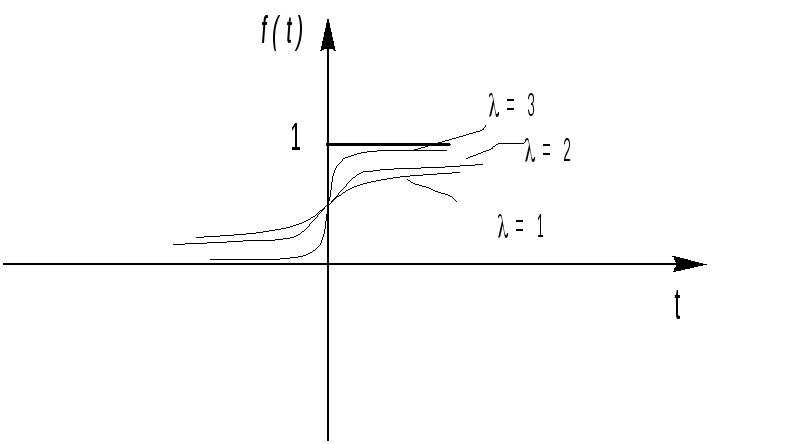
Последовательность непрерывных функций

при λ→ ∞ также имеет своим пределом первое представление 1(t).