
Физика (4 семестр) / Лекция 5
.pdfАлек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
1 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Лекция № 5
Тема лекции:
Теория Бора и квантово-механическая теория атома
Рассматриваемые вопросы:
1.Постулаты Бора……………………………………………………………………1
2.Теория Бора для водородоподобных систем………………………...…………..7
3.Экспериментальное подтверждение постулатов Бора…………………………10
4.Водородоподобная система в квантовой механике……….………………..…..16
5.Основное состояние атома водорода……………………………………….……19
1. ПОСТУЛАТЫ БОРА
От открытия сериальных закономерностей в атоме водорода до квантово-механического решения задачи об атоме водорода физика прошла огромный путь, исторически очень короткий, но полный драматизма и выдающихся открытий. Этот путь, как и вся физика первой половины XX века, всегда будет связан с именем великого физика — датчанина Нильса Бора.
В предыдущей лекции было показано, что дискретный линейчатый спектр атома водорода находятся в прямом противоречии с классическим истолкованием модели атома Резерфорда.
Первая попытка построения неклассической теории атома была предпринята Н. Бором (1913) и составила важный этап в развитии современной физики. В основе этой теории лежала идея связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атомов Резерфорда и квантовый
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
2 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
характер излучения и поглощения света, подтвержденные обширным экспериментальным материалом.
В теории Бора не содержалось принципиального отказа от описания поведения электрона в атоме с помощью законов классической физики. Такое описание сохранялось. Однако для достижения тех целей, которые поставил перед собой Бор, ему пришлось дополнить классическое описание некоторыми ограничениями, накладываемыми на возможные состояния электронов в атоме. Эти ограничения были сформулированы в виде постулатов, физический смысл которых не только не мог быть объяснен в рамках теории, но, более того, противоречил сохраняющемуся в теории классическому описанию движения электрона в атоме.
Тем не менее, такой принципиально непоследовательный путь привел к правильным результатам в некоторых вопросах, в частности к объяснению спектральных закономерностей атома водорода. Причина этого заключается в том, что в боровской теории, которую часто называют «старой» квантовой теорией, были правильно указаны некоторые свойства атомных систем. Как мы увидим, эти правильные результаты могут быть получены в квантовой механике из гораздо более строгих и общих положений, не требующих постулатов.
Теория Бора применима не только к атому водорода, но и к водородоподобной системе, состоящей из ядра с зарядом
Ze и одного электрона, вращающегося вокруг ядра. Такую систему называют изоэлектронной водороду. Примерами
таких систем являются ионы Не+, Li++ и др.

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
3 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Первый постулат Бора (постулат стационарных состояний) заключается в следующем:
существуют стационарные состояния атома, находясь в которых он не излучает энергию, при этом электрон, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию
(1)
Здесь те — масса электрона; v — скорость электрона; r — радиус его орбиты.
Этим стационарным состояниям соответствуют вполне определенные (стационарные) орбиты, по которым движутся электроны. При движении по стационарным орбитам электроны, несмотря на наличие у них ускорения, не излучают электромагнитных волн.
Целое число п равно числу длин волн де Бройля для электрона, укладывающихся на длине круговой орбиты. В самом деле, учитывая формулу де Бройля, найдем отношение длины окружности к длине волны де Бройля:
Второй постулат (правило частот) устанавливает, что
при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон.
(2)
где Wn и Wm — энергия атома в двух стационарных состояниях.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
4 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
При Wm < Wn происходит излучение фотона, при Wm > Wn
— его поглощение.
Другими словами, излучение происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией (при переходе электрона с орбиты более
удаленной от ядра на ближнюю к ядру орбиту). Поглощение фотона сопровождается переходом атома
в состояние с большей энергией. Этому соответствует переход электрона на более удаленную от ядра орбиту.
Анализируя содержание постулатов Бора, нельзя не заметить, что первый и второй постулаты связаны с невозможностью классического обоснования ядерной модели атома, а также со спектральными закономерностями в атоме водорода и квантовой структурой излучения.
В самом деле, сопоставление формулы (2) с сериальной формулой для спектра водорода (см. предыдущую лекцию)
(3)
позволяет сделать заключение о том, что энергия атома в некотором стационарном состоянии
(4)
Постоянная Ридоерга была вычислена из принципа соответствия Бора. Спектральный терм связан с энергией атома формулой
(5)

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
5 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Таким образом, целые числа, входящие в сериальные формулу (3), определяют квантованные значения энергии атома (энергетические уровни атома водорода).
Целое число п, определяющее энергетические уровни водородного атома по формуле (4), называется
главным квантовым числом.
Из формулы (4) следует, что энергетические состояния атома водорода образуют последовательность энергетических уровней, изменяющихся в зависимости от п.
Энергетическое состояние, соответствующее n = 1 ,
называется основным, или нормальным
(невозбужденным), состоянием.
Все состояния с п > 1 называются возбужденными.
При возрастании n энергетические уровни сближаются к границе, соответствующей n = ∞ . При этом n имеем W∞ = 0 . Знак минус в формуле (4) показывает, что электрон связан в атоме силой притяжения к ядру. Поэтому абсолютное значение Wn в формуле (4) считают
энергией связи электрона в атоме, находящемся в состоянии п.
Состояние n = ∞ соответствует ионизации атома, т. е. отрыву от него электрона.
Энергия ионизации из данного состояния равна энергии связи электрона в атоме в этом состоянии. Энергия ионизации Wион связана с потенциалом ионизации ϕ :
Wион = eϕ . Таким образом,
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
6 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Потенциал |
ионизации |
атома |
водорода |
из |
нормального состояния (n = 1) составляет |
|
|
||
|
ϕ = Rh e |
|
|
(6) |
Подставив в (6) значения всех постоянных (значение |
||||
R должно быть |
взято с учётом ядра), |
получим |
для |
|
потенциала ионизации атома водорода из нормального состояния ϕ = 13,60 В.
Рис. 1.
На рис. 1 приведена схема энергетических уровней атома водорода (W = Wn − W1 ). Стрелками указаны переходы, соответствующие излучению различных серий линий ( λ в нм).

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
7 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
2. ТЕОРИЯ БОРА ДЛЯ ВОДОРОДОПОДОБНЫХ СИСТЕМ
На основе постулатов (1) и (2) Бор построил теорию для водородоподобных систем.
Правило частот не могло быть навеяно никакими эмпирическими формулами, оно было постулировано Бором. Это правило (1) в соединении с формулой (2) позволили Бору рассчитать спектр атома водорода и других изоэлектронных водороду систем, а также теоретически вычислить соответствующие им значения постоянной Ридберга, находящиеся в хорошем согласии с опытом.
Бор считал, что движение электрона в водородоподобной системе происходит по круговой орбите радиуса r под действием кулоновской силы притяжения электрона к ядру, обусловливающей центростремительное ускорение, т.е. можно записать
mev2  r = Ze2
r = Ze2  (4πε 0r2 ),
(4πε 0r2 ),
или, помножая обе части уравнения на mer :
4πε |
0 |
m2v2r2 = m Ze2r . |
(7) |
||
|
|
e |
e |
|
|
Из (7) с учётом |
|
первого постулата Бора |
(1), |
||
|
|
|
|
, получим |
|
(8)
При n = 1 для водорода (Z= 1) имеем
(9)
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
8 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Эту величину называют радиусом первой орбиты электрона в атоме водорода (первым боровским радиусом).
Из формулы (8) видно, что радиусы орбит увеличиваются пропорционально квадратам целых чисел. Энергия электрона в водородоподобной системе равна сумме его кинетической WК и потенциальной WП , энергий в электростатическом поле ядра:
|
(10) |
Подставив r в (10) из (8), получим |
|
|
(11) |
Для атома водорода (Z = 1) |
|
|
(12) |
Из сравнения формул (12) и (4) ( |
) |
следует, что постоянная Ридберга |
|
(13)
Соответственно формулу (11) для энергетических уровней водородоподобной системы можно переписать в виде:
(14)
Учет движения ядра сводится к тому, что вместо массы те электрона в формулу (13) следует ввести приведенную массу mприв двух частиц электрона и ядра, движущихся от-
носительно центра масс системы ядро — электрон:

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
9 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
mприв = meM ,
me + M
где М — масса ядра атома.
Бор также предложил более общий подход для вычисления постоянной Ридберга при n >> 1 , который привёл к такому же результату, как и формула (13).
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
10 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
3. ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ ПОСТУЛАТОВ БОРА
Постулат Бора о существовании стационарных состояний атомов и правило частот нашли свое экспериментальное подтверждение в опытах Д. Франка и Г. Герца (1913). В опытах изучались столкновения электронов с атомами газов методом задерживающего потенциала. Идея опытов заключалась в том, что пучок электронов, ускоряемых в электрическом поле, проходил через газ, и электроны испытывали соударения с атомами газа. Первые опыты были поставлены на ртути.
Рис. 2.
Опыт. Накаленный катод К (рис. 2), испускающий электроны; сетчатый электрод S и анод А, соединенный с электрометром или гальванометром G, помещались в стеклянный сосуд, в котором находились ртутные пары при давлении около 0,1 мм рт. ст. Между катодом и сеткой создавалось ускоряющее электрическое ноле с разностью потенциалов ϕ1 а между сеткой и анодом — слабое
замедляющее поле с разностью потенциалов ϕ2 , не превышающей 0,5 В.
Электроны, встречающие на своем пути атомы ртути, могут испытывать с ними соударения двоякого рода. Первый тип соударений — упругие столкновения, в
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
11 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
результате которых энергия электронов не изменяется, а изменяются лишь направления скоростей электронов. Такие упругие столкновения, хотя и затрудняют попадание электронов на анод, не могут быть причиной практически полного отсутствия анодного тока в трубке, который должен возрастать с увеличением разности потенциалов ϕ1 . Второй тип возможных соударений электронов с атомами
— неупругие столкновения — связан с потерей электронами их энергии и передачей этой энергии атомам ртути. В соответствии с постулатами Бора каждый из атомов ртути не может принять энергию в любом количестве. Атом может воспринять лишь определенную энергию и перейти при этом в одно из возбужденных энергетических состояний.
Ближайшее к нормальному состоянию атома ртути возбужденное состояние отстоит от основного по шкале энергий на 4,86 эВ. До тех пор, пока электроны, ускоряемые полем, не приобретут энергию eϕ1 = 4,86 эВ, они испытывают лишь упругие столкновения и анодный ток возрастает с ростом ϕ1 . Как только кинетическая энергия электронов достигает 4,86 эВ, начинают происходить неупругие столкновения. Электрон с таким значением энергии полностью отдает ее атому ртути, возбуждая переход одного из электронов атома ртути из нормального энергетического состояния на возбужденный энергетический уровень. Ясно, что такой электрон, потерявший свою кинетическую энергию, не сможет преодолеть задерживающее его поле, и не достигнет анода.
Таким образом, при разности потенциалов между катодом и сеткой, равной 4.86 эВ, должно происходить резкое падение анодного тока. Аналогичное явление будет при eϕ1 = 2 4,86
эВ, eϕ1 = 3 4,86 эВ, вообще говоря, при eϕ1 = n 4,86 эВ,
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
12 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
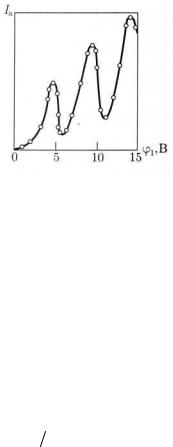
когда электроны могут испытать два, три и т. д. неупругих соударения с атомами ртути, потерять при этом полностью свою энергию и не достигнуть анода. На рис. 3 приведена характерная кривая зависимости силы анодного тока от разности потенциалов между катодом и сеткой в опытах Франка и Герца, подтверждающая справедливость первого постулата Бора.
Рис. 3.
Правило частот Бора также экспериментально подтвердилось в опытах Франка и Герца. Ртутные пары, возбужденные электронным ударом, оказались источником ультрафиолетового излучения с длиной волны 2537 А (первая резонансная линия ртути). Это излучение происходит в тот момент, когда атом ртути, возбужденный электронным ударом на уровень с энергией W2, возвращается в основное нормальное энергетическое состояние с энергией
W1 . Согласно правилу |
частот |
Бора, |
W2 − W1 = hν , |
где |
|
W2 − W1 = |
W . По известному |
значению W = 4,86 |
эВ |
||
можно вычислить длину волны излучения: |
|
||||
|
λ = hν |
W = 2,537 10−7 |
м. |
|
|
Этот |
результат |
полностью |
согласуется |
с |
|
экспериментом. |
|
|
|
|
|
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
13 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Серьезным успехом теории Бора явились теоретическое вычисление постоянной Ридберга для водородоподобных систем и объяснение структуры их линейчатых спектров. В частности, Бору удалось правильно объяснить серии спектральных линий ионизированного гелия, до этого приписываемые водороду (серии Пикеринга и Фаулера для Не+).
По значениям постоянной Ридберга R для Н и Не+ можно теоретически вычислить отношение массы протона к массе электрона тр/те и значение RH при неподвижном ядре. Вычисления привели к значению тр/те = 1847, находящемуся в согласии с известным из опыта. Это было очень важным подтверждением правильности основных идей, содержавшихся в теории Бора.
Не менее важным оказалось нахождение удельного заряда электрона е/те из спектроскопических данных. Значение е/те определяется по известным постоянным Ридберга для двух различных атомов, например водорода и дейтерия (тяжелого водорода).
Теория Бора объяснила физическую природу характеристических рентгеновских спектров, расщепление спектральных линий в сильном магнитном поле (нормальный эффект Зеемана) и другие явления. Дальнейшее обобщение правил квантования орбит на системы со многими степенями свободы позволило установить, что состояние электрона в водородоподобной системе не может быть описано одним квантовым числом. Квантовых чисел должно быть столько же, каково число
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
14 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
степеней свободы, например для эллиптической орбиты электрона их должно быть два.
Теория Бора сыграла огромную роль в создании атомной физики. В период ее развития (1913—1925) были сделаны важные открытия, навсегда вошедшие в сокровищницу физической науки.
Особенно велика ее роль в развитии атомной, а также частично и молекулярной спектроскопии, где огромный экспериментальный материал с помощью теории Бора был систематизирован и сведен к определенным полуэмпирическим закономерностям.
Однако наряду с определенными успехами в теории Бора с самого начала обнаружились существенные недостатки. Главнейшим из них была внутренняя противоречивость теории. Основываясь на механическом соединении классической физики с квантовыми постулатами, теория Бора в ряде проблем привела к существенным трудностям. Сюда прежде всего относится вопрос об интенсивностях спектральных линий. Для их вычисления в теории Бора приходилось применять принцип соответствия не только для больших квантовых чисел, но и для малых, т. е., по существу, использовать для расчета интенсивностей классические представления. Наиболее серьезной неудачей в теории Бора явилась абсолютная невозможность с ее помощью создать теорию атома гелия, содержащего помимо ядра два электрона. Постепенно становилось очевидным, что теория Бора, правильно объяснившая одни факты и не способная истолковывать целый ряд других, представляет собой лишь переходный этап на пути создания последовательной
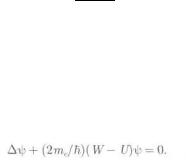
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
15 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
теории атомных и ядерных явлений. Такой последовательной теорией явилась квантовая (волновая) механика. Применение ее к атомным процессам позволило не только объяснить огромное многообразие явлений атомной и ядерной физики, но и вскрыть физическое содержание самих постулатов Бора.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
16 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
4. ВОДОРОДОПОДОБНАЯ СИСТЕМА В КВАНТОВОЙ МЕХАНИКЕ
Результаты, достигнутые теорией Бора в решении задачи об энергетических уровнях электрона в водородоподобной системе, получены в квантовой механике без привлечения постулатов Бора.
Рассмотрим движение электрона в кулоновском поле ядра Ze, т.е. задачу об электроне, обладающем потенциальной энергией
U(r) = − Ze2 , 4πε 0r
где r — расстояние между электроном и ядром.
Состояние электрона в водородоподобном ионе описывается некоторой волновой функцией ψ , удовлетворяющей стационарному уравнению Шредингера:
(15)
Здесь W — значения полной энергии электрона в ионе, которые требуется отыскать при условии, что ψ удовлетворяет требованиям конечности, однозначности и непрерывности.
Центрально-симметричный характер силового ноля, в котором движется электрон, естественно, требует использования сферических координат при решении уравнения (15). Это уравнение имеет вид:

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
17 |
|||||||||||||||||||||||||||
Лекция № 5. Теория Бора и квантово-механическая теория атома |
|
|||||||||||||||||||||||||||
|
1 ∂ |
2 |
|
∂ψ |
|
|
1 |
|
|
∂ |
|
|
|
|
∂ψ |
|
||||||||||||
|
|
|
|
|
|
|
r |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
sinϑ |
|
|
+ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
r2 |
|
∂r |
|
|
∂r |
|
r2 sinϑ ∂ϑ |
|
|
|
∂ϑ |
(16) |
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
2me |
|
|
|
Ze |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
∂ ψ |
|
|
|
|
|
|
|
|
||||||||||||
+ |
r |
2 |
sinϑ |
∂ϕ |
2 |
+ |
|
|
2 |
|
W + |
4πε |
|
ψ = 0 |
|
|||||||||||||
|
|
|
|
|
|
|
h |
|
|
|
0r |
|
|
|
||||||||||||||
Решение уравнения (16) в сферических координатах выходит за рамки данного курса общей физики, и здесь приводятся лишь окончательные результаты.
Собственные функции уравнения (16) содержат три
целочисленных параметра: |
|
ψ = ψ nlm(r,ϑ,ϕ ) , |
(17) |
где n – главное квантовое число;
l – орбитальное квантовое число (азимутальное кв.ч.); m – магнитное квантовое число.
Момент импульса электрона в ионе квантуется по формуле
(16)
где l = 0; 1; 2;K; (n− 1) — орбитальное квантовое число.
Из уравнения (15) следует, что при W< 0, т. е. в условиях, когда электрон «связан» в атоме, его движения должны быть периодическими, а значения W — полной энергии — квантованными. Энергия, которой может обладать электрон в ионе,
(17)
где nr — радиальное квантовое число.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
18 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
Если ввести обозначение
(18)
то выражение (17) для энергетических уровней электрона в водородоподобной системе можно записать в форме, аналогичной выражению (12) в теории Бора:
(19)
Таким образом, последовательное решение уравнения Шредингера для электрона в водородоподобной системе приводит к энергетическим уровням типа Бальмера— Ридберга без использования каких-либо постулатов. Квантовое число п, определенное по формуле (18), совпадает с главным квантовым числом, вводимым в теории Бора.
Энергетические уровни электрона для водородоподобной системы зависят только от главного квантового числа. Из формулы (18) следует, что наибольшему значению lmax при данном n соответствует
nr = 0 , т.е. lmax = n− 1 . Следовательно, при заданном n орбитальное квантовое число может принимать следующие значения:
(20)

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
19 |
Лекция № 5. Теория Бора и квантово-механическая теория атома
5. ОСНОВНОЕ СОСТОЯНИЕ АТОМА ВОДОРОДА
Состояние электрона, обладающего различными значениями орбитального квантового числа, в атомной физике принято обозначать и называть следующим образом:
l = 0 — s-состояние, l = 0 — p-состояние l = 0 — d -состояние
l = 0 — f -состояние и т. д. в порядке следования букв латинского алфавита.
Рассмотрим более подробно s-состояние электрона в
атоме водорода при n = 1 . Такое состояние электрона и атома называется основным.
Волновая функция электрона в этом состоянии является функцией только r : ψ =ψ (r) , т.е. s-состояние электрона в атоме сферически симметрично, плотность вероятности обнаружить электрон в данной точке атома будет зависеть только от r . Уравнение Шредингера для основного состояния водородного атома имеет вид
|
|
(21) |
Будем искать решение этого уравнения в форме |
|
|
ψ = ce− r a0 |
|
(22) |
где a0 имеет размерность длины; |
c — |
некоторая |
постоянная, определяемая из условия нормировки вероятности.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
20 |
Лекция № 5. Теория Бора и квантово-механическая теория атома |
|
Дифференцируя ψ (22) и подставляя dψ dr |
и |
d2ψ dr2 в (21), получим после сокращения ce− r a0 |
|
(23)
Последнее уравнение удовлетворяется для любых значений r при выполнении двух условий:
|
(24) |
Из последнего условия следует, что |
|
|
(25) |
Из сравнения (25) с (9) |
видно, что |
выражение (25) совпадает с первым боровским радиусом a0
для атома водорода. Подставив (25) в (12), найдем
(26)
Это соответствует значению энергии основного состояния атома водорода (n = 1).
Найдем вероятность того, что электрон в основном состоянии атома водорода находится на расстоянии r от ядра, точнее — в интервале расстояний от r до r + dr , т. е. в шаровом слое объемом
dV = 4πr2dr .
Вероятность обнаружить электрон в элементе объема dV имеет вид
