
Физика (4 семестр) / Лекция 6
.pdf
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
1 |
Лекция № 6. Методы квантования |
|
Лекция № 6
Тема лекции:
Методы квантования
Рассматриваемые вопросы:
1.Приближенный метод квантования энергии электрона в атоме водорода…….1
2.Пространственное квантование. Опыты Штерна и Герлаха.……...……………5
3.Спин электрона……………………………………………………………………13
4.Квантование спина………………………………………………………………..17
1. ПРИБЛИЖЕННЫЙ МЕТОД КВАНТОВАНИЯ ЭНЕРГИИ ЭЛЕКТРОНА В АТОМЕ ВОДОРОДА
Для произвольного состояния электрона, обладающего потенциальной энергией
U(r) = − |
e2 |
|
|
|
r2 |
||
|
4πε |
0 |
|
|
|
|
|
в поле ядра атома водорода, решение уравнения Шредингера представляет большие трудности. Вместе с тем очень важно получить энергетические уровни Wn электрона в атоме водорода в форме, полученной ранее:
1 |
|
Z2m e4 |
|
|||
Wn = − |
|
|
e |
|
. |
(1) |
n2 |
|
8h2ε |
2 |
|||
|
|
|
|
0 |
|
|
Попытаемся качественно получить эту формулу по методу, аналогичному тому, который применен для гармонического осциллятора.
Будем исходить из того, что на эффективной длине в области, дозволенной «потенциальной ловушкой»
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
2 |
Лекция № 6. Методы квантования |
|
(отрезки ab, a′b′ , a′′b′′ и т. д. на рис. 1), должно укладываться целое число полуволн де Бройля.
Рис. 1.
Поскольку эффективная длина l, проецируемая на ось r , рис. 1, зависит от энергии W, форма потенциальной кривой определит квантование энергии. Из равенства потенциальной энергии на «стенках» потенциального ящика (потенциальной ловушки), т.е. в точках a, a′ , a′′ , b, b′ , b′′ и т.д., энергии W имеем
(2)
Эффективную длину волны де Бройля λэф введем по формуле:
(3)
Для определения λэф воспользуемся соотношениями:
(4)
и
(5)
Задача сводится к отысканию  U
U , которое нельзя
, которое нельзя
провести элементарными методами.

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
3 |
Лекция № 6. Методы квантования |
|
В данном курсе общей физики сделаем упрощающее предположение о том, что электрон может с равной вероятностью находиться в любом месте внутри «потенциальной ловушки». В этом случае бесконечно малый заряд внутри сферического слоя радиусом r и толщиной dr равен
Потенциальная энергия этого слоя в поле ядра, заряд которого e, равна
Среднее значение потенциальной энергии
Теперь формула (4) принимает вид
(6)
С другой стороны, принимая во внимание (5) и (2) имеем
Подставив это значение λэф в (6), получим после сокращения
(7)
Сравним эту формулу с выражением (1). Как видно, зависимость энергии от главного квантового числа и универсальных постоянных т, е, h получилась правильной. Единственное отличие от точной формулы состоит в том, что вместо восьмерки в знаменателе стоит π 2 = 9,98.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
4 |
Лекция № 6. Методы квантования |
|
Разумеется, приведенные рассуждения не следует считать выводом выражения для энергии водородного атома. Их цель — иллюстрировать зависимость энергий Wn от формы потенциальной кривой и показать, что электрон, обладающий волновыми свойствами и движущийся в кулоновском поле ядра в атоме водорода, имеет квантованные значения энергии Wm обратно пропорциональные квадрату главного квантового числа п2.

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
5 |
Лекция № 6. Методы квантования |
|
2. ПРОСТРАНСТВЕННОЕ КВАНТОВАНИЕ. ОПЫТЫ ШТЕРНА И ГЕРЛАХА
Согласно представлениям классической физики
электроны в атоме движутся по замкнутым траекториям — орбитам, образуя систему замкнутых орбитальных
токов. Пусть электрон движется со скоростью v по круговой орбите радиуса r (рис. 2).
Рис. 2.
Сила орбитального тока равна
(8)
где е — элементарный заряд; v — частота обращения электрона по орбите. Направление орбитального тока показано на рис. 2 стрелкой.
Орбитальному току соответствует магнитный момент pm , называемый орбитальным магнитным моментом электрона.
Вектор pm направлен перпендикулярно плоскости орбиты электрона (см. рис. 2), а его модуль
(9)
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
6 |
Лекция № 6. Методы квантования |
|
где S = πr2 — площадь орбиты.
Момент импульса Le электрона, движущегося по орбите, относительно ее центра О называется орбитальным моментом импульса электрона:
(10)
где т — масса электрона; r — его радиус-вектор, проведенный из центра О орбиты. Вектор Le противоположен по направлению вектору рm:
(11)
где получаемое из (9) и (11) коэффициент –
(12)
— гиромагнитное (магнитомеханическое) отношение орбитальных моментов электрона.
Таким образом, орбитальный момент импульса электрона Ll , и пропорциональный ему магнитный момент pm ориентированы перпендикулярно плоскости орбиты электрона и направлены в противоположные стороны.
Между векторами pm и Ll , имеется связь
(13)
Аналогичная связь существует между магнитным моментом и механическим моментом импульса атома в
целом. Указанная связь векторов pm и Ll , выводится в
классической физике и сохраняется в теории Бора. В квантовой механике, естественно, не может быть указана
ориентация векторов pm и Ll относительно плоскости электронной орбиты. Для указания ориентации векторов pm
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
7 |
Лекция № 6. Методы квантования |
|
и Ll должно быть выбрано некоторое направление в пространстве, и расположение вектора Ll , фиксируется углом между вектором Ll и направлением, за которое
выбирается направление любого внешнего магнитного поля, в котором находится атом и его электроны, либо внутреннего магнитного поля, созданного всеми электронами (кроме рассматриваемого) и ядром атома. В классической физике
предполагалось само собой разумеющимся, что вектор Ll
(или pm ) может быть ориентирован относительно из-
бранного направления магнитного поля произвольным образом. На этом естественном предположении основывалась классическая теория парамагнетизма П. Ланжевена.
На языке теории Бора возможность любых ориентации вектора означает, что плоскость орбиты электрона может быть ориентирована произвольно по отношению к внешнему магнитному полю. Однако такое
предположение было ошибочным. Оказалось, что существует так называемое пространственное квантование:
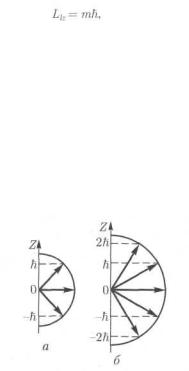
момент импульса электрона может иметь лишь такие ориентации в пространстве, при которых проекция Llz
вектора Ll на направление Z внешнего поля принимает квантованные значения, кратные h .
Этот результат впервые был получен как следствие обобщенных А. Зоммерфельдом правил квантования боровских орбит. В квантовой механике строго доказано,
что проекция Llz вектора Ll , орбитального момента
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
8 |
Лекция № 6. Методы квантования |
|
импульса электрона на направление Z внешнего магнитного поля принимает лишь целочисленные значения h :
(14)
где т = 0, ±1, ±2, ±3,..., ±l— магнитное квантовое число
( l— орбитальное квантовое число, определяющее модуль вектора Ll ).
Таким образом, вектор Ll может принимать 2l + 1
ориентации в пространстве. На рис. 3 приведены возможные ориентации векторов Ll , для электронов в р- и d-состояниях ( l = 1 и l =2).
Рис. 3.
О. Штерном и В. Герлахом были поставлены опыты (1922), целью которых являлось измерение магнитных моментов pm атомов различных химических элементов.
Для определения моментов Ll и pm одного
электрона опыты должны быть поставлены с атомами, у которых орбитальные механические (и магнитные)

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
9 |
Лекция № 6. Методы квантования |
|
моменты всех электронов, кроме одного, взаимно компенсируют друг друга. Такими атомами являются атомы химических элементов, образующие первую группу периодической системы Менделеева и имеющие один валентный электрон на внешней оболочке.
Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле. В таком магнитном поле на атом должна действовать сила
(15)
Здесь В — индукция магнитного поля (направленная вдоль оси Z), неоднородного только вдоль этой же оси.
Опыты Штерна и Герлаха обнаружили ошибочность классического предположения о том, что магнитный момент
pm и механический момент импульса Ll , атома произвольно
ориентируются относительно направления внешнего поля, и подтвердили наличие пространственного квантования. Схема первых опытов Штерна и Герлаха изображена на рис. 4.
Рис. 4.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
10 |
Лекция № 6. Методы квантования |
|
Опыт. В трубке, где был создан вакуум порядка 10-5 мм рт. ст., помещался источник пучка атомов — нагреваемый до высокой температуры серебряный шарик К. Атомы серебра вылетали с его поверхности со средней тепловой скоростью порядка 100 м/с, соответствующей температуре испарения серебра. Из этих атомов с помощью щелевых диафрагм В вырезался узкий пучок, проходящий через сильное и неоднородное магнитное поле, направленное перпендикулярно пучку. Основная трудность опыта состояла в том, чтобы достигнуть такой большой неоднородности магнитного поля, которая сказывалась бы на расстояниях порядка размеров атома. При такой величине неоднородности поля, согласно формуле (15), можно было рассчитывать на получение значительной отклоняющей силы F, действующей на атом в магнитном поле. Необходимая неоднородность поля была достигнута в результате применения сильного электромагнита SN c полюсными наконечниками специальной формы. Приемником атомов серебра служила фотопластинка А.
Если бы момент импульса Ll атома (и его магнитный момент pm ) мог бы принимать произвольные ориентации в
магнитном поле, то можно было ожидать непрерывного распределения попаданий атомов на пластинку с большей плотностью попаданий в середине пластинки и меньшей плотностью к ее краям. Опыты, проведенные с серебром и атомами других элементов периодической системы, привели к совершенно другому результату. На рис. 5 показана фотография результата опыта Штерна и Герлаха с литием.
Рис. 5
Из рисунка видно, что на фотопластинке получились две резкие полосы — все атомы отклонялись в магнитном поле двояко, что соответствовало лишь двум возможным
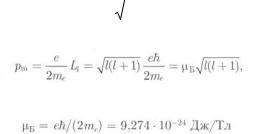
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
11 |
Лекция № 6. Методы квантования |
|
ориентациям магнитного момента во внешнем поле. Момент импульса атома (и его магнитный момент) равен суммарным моментам электронов, поскольку магнитные моменты ядер значительно меньше по модулю, чем магнитные моменты электронов. Последние совпадают с суммарными моментами валентных электронов, так как моменты электронов заполненных оболочек компенсируются.
У лития и других атомов первой группы периодической системы имеется один валентный оптический электрон. Таким образом, моменты импульса и магнитные моменты таких атомов совпадают с моментами электрона.
Если подставить полученное ранее выражение
Ll |
= |
|
l(l + 1) |
h |
(16) |
в (13), то связь величин |
pm |
и Ll можно записать в виде |
|||
(17)
где Б – магнетон Бора:
Таким образом, магнитный момент может содержать некоторое число 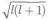 магнетонов Бора.
магнетонов Бора.
По известной величине dB/dz неоднородности магнитного поля, направленного по оси Z, и по определенной из отклонения атомов в магнитном поле силе F, действующей на атом, можно, пользуясь формулой (15), найти pmz .
Для серебра Штерн и Герлах получили, что проекция магнитного момента атома на направление поля численно
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
12 |
Лекция № 6. Методы квантования |
|
равна магнетону Бора. По оценкам исследователей, относительная погрешность в определении магнитного момента не превышала 10 %. Результаты этих опытов, впоследствии проверенные на других атомах элементов первой группы периодической системы, не вызывают ни малейшего сомнения.
Таким образом, опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульса в магнитном поле, но, кроме того, экспериментально подтвердили вывод о том, что магнитные моменты электронов и атомов состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу, связанную с квантованием момента импульса. Магнитные моменты электронов и атомов выражаются в магнетонах Бора.
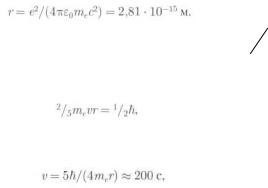
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
13 |
Лекция № 6. Методы квантования |
|
3. СПИН ЭЛЕКТРОНА
Важной особенностью атомов первой группы элементов таблицы Менделеева, с которыми ставились вначале опыты Штерна и Герлаха, является то, что валентный электрон в основном состоянии атома имеет орбитальное квантовое число, равное нулю, т. е. электрон находится в s-состоянии. Атомный пучок в опытах содержал атомы, находящиеся в основном состоянии. Однако в состоянии с l= 0 электрон не имеет момента импульса, как это следует из формулы (17). Поэтому возникает серьезный вопрос об истолковании результатов опытов Штерна и Герлаха. Пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна одному магнетону Бора? Ранее Эйнштейн и де Гааз обнаружили аномальное значение гиромагнитного отношения для ферромагнетиков. Для объяснения этих результатов нужно предположить, что у электрона помимо
орбитального момента импульса Ll и соответствующего ему магнитного момента pm имеются собственный
механический момент импульса Ls , называемый спином электрона, и соответствующий ему собственный магнит ный момент pms .
Предположение о существовании спина было высказано (1925) С. Гаудсмитом и Дж. Уленбеком в связи с целым рядом трудностей в атомной физике, накопившихся к тому времени. Одной из них, и притом очень важной, явилась трудность с истолкованием результатов опытов Штерна и Герлаха.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
14 |
Лекция № 6. Методы квантования |
|
Уленбек и Гаудсмит дали спину электрона наглядное модельное истолкование, заключающееся в том, что спин рассматривается как момент импульса, связанный с вращением электрона — заряженного шарика — вокруг своей оси. Однако можно показать, что такое представление о спине приводит к противоречию с теорией относительности.
Оказывается, что для того, чтобы вращающийся вокруг
своей оси |
электрон-шарик приобрел магнитный |
мо |
|||
мент, равный одному магнетону Бора, угловая |
скорость |
||||
вращения |
должна |
быть |
такой, |
чтобы |
|
линейная скорость на поверхности сферы в |
200 |
раз |
|||
превосходила скорость света в вакууме. |
|
|
|
||
В самом деле, предположим, что электрон представляет собой шарик с некоторым радиусом г. Величину этого «классического» радиуса электрона можно оценить, приравняв потенциальную энергию заряженного шарика его собственной энергии
e2 |
|
= m c2 . |
|
|
|
4πε |
0r |
e |
|
Отсюда следует, что классический радиус электрона
Если шарик радиусом r с моментом инерции J = 2 5 mer2
вращается с угловой скоростью ω = v r, то, приравнивая момент импульса Jω спину электрона, получим
r, то, приравнивая момент импульса Jω спину электрона, получим
где v— линейная скорость на экваторе шарика. Простая оценка показывает, что при этом
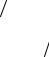
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
15 |
Лекция № 6. Методы квантования |
|
а это находится в очевидном противоречии с теорией относительности. Модельное представление о спине при всей его наглядности не выдерживает критики и к нему не следует привыкать – советует современная физика.
Однако, может быть физика будущего вернётся к модельному представлению.
Если представить электрон в виде тора с малым радиусом r и большим радиусом R = D K , где D K – комптонова длина, и полагать, что массу определяет величина r , а магнитный момент – R, то можно записать для механического момента
J = m D |
2 |
|
, |
|||
|
|
e |
K |
|
|
|
и для скорости |
|
|
|
|
|
|
ω = v D K . |
||||||
Тогда получим |
|
|
|
|
|
|
Jω = meD Kv = h 2 , |
||||||
откуда следует |
|
|
|
|
|
|
v = |
|
h |
|
|
|
. |
|
|
|
|
|
||
2meD K |
|
|||||
|
|
|
||||
Учитывая, что |
|
|
|
|
|
|
D K = |
h |
|
|
, |
||
|
|
|
||||
mec
то окончательно имеем:
v = c 2 .
2 .
Такой модельный подход не противоречит требованиям максимальности скорости.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
16 |
Лекция № 6. Методы квантования |
|
Спин электрона и других элементарных частиц в
настоящее время рассматривают как некоторое особое свойство этих частиц: подобно тому, как частицы имеют
массу, а заряженные частицы — заряд, они имеют еще и спин. Заметим, что в дальнейшем развитии квантовой механики Дираку удалось показать, что существование спина вытекает из полученного им релятивистского волнового уравнения.

Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
17 |
Лекция № 6. Методы квантования |
|
4. КВАНТОВАНИЕ СПИНА
Если приписать электрону собственный момент импульса Ls (сокращенно — спиновый момент, или просто спин), то с ним оказывается связанным некоторый собственный магнитный момент pms электрона. Из общих
выводов квантовой механики следует, что спин должен быть квантован по закону
(17)
где s — квантовое число, называемое спиновым квантовым числом.
Проекция Lsz спина на ось Z, совпадающую с направлением внешнего магнитного ноля, должна быть
квантована и вектор Ls , может иметь 2s+1 различных ориентации в магнитном поле.
Из опытов Штерна и Герлаха следует, что для спина электрона таких ориентациq существует всего 2, так что
2s+ 1 = 2 ,
т. е.
s = 1 2
Для атомов первой группы периодической системы, валентный электрон которых находится в состоянии с l = 0, момент импульса всего атома равен спину валентного электрона. Поэтому обнаруженное для таких атомов пространственное квантование момента импульса атома в магнитном поле явилось доказательством наличия у спина лишь двух ориентации во внешнем поле.
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
18 |
Лекция № 6. Методы квантования |
|
Спиновое квантовое число в отличие от введенных ранее трех квантовых чисел — главного п, орбитального l и магнитного т — не является целым числом. Числовое значение спина электрона найдем по формуле
(18)
По аналогии с пространственным квантованием орбитального момента импульса электрона Ll , проекция Lsz
вектора Ls , на направление внешнего поля должна быть
квантованной величиной и определяться по формуле, аналогичной (14):
(19)
где число ms может иметь всего два значения: тs = ±1/2.
Следует отметить, что Число т, по аналогии с т можно было бы назвать магнитным спиновым числом. Однако такое название обычно редко
применяется. Число тs, отличается от s только тем, что может принимать два значения: не только +1/2, но и —1/2. Гораздо чаще, говоря о спиновом квантовом числе, понимают под ним число тs, т.е. приписывают спиновому квантовому числу значения ±1/2. Следует, однако, помнить, что число s имеет только одно значение: s = ½ .
Таким образом, проекция спинового механического момента импульса на направление поля может принимать два значения:
(20)
Часто полагают, что спин электрона может быть ориентирован либо вдоль направлени напряженности
магнитного поля, либо противоположно вектору Н. Такое общепринято словоупотребление неточно: говоря о направлении спина, при этом в действительности имеют в виду направление его составляющей Lsz .
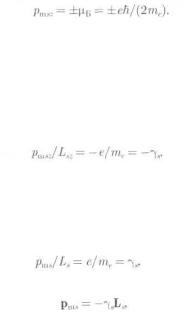
Алек Власов, профессор каф. ОиЭФ (ФЭ, 4-й сем. 2007/2008). |
19 |
Лекция № 6. Методы квантования |
|
Из опытов Штерна и Герлаха следует, что проекция pmsz собственного магнитного момента электрона равна плюс или минус магнетон Бора µБ :
(21)
Часто считают, что собственный магнитный момент электрона равен магнетону Бора. Это тоже неточность:
говоря о магнитном моменте, при этом в действительности имеют в виду абсолютное значение его проекции на
направление магнитного поля. Из формул (20) и (21) видно, что
(22)
Очевидно, что отношение числовых значений проекций векторов, направленных во взаимно противоположные стороны, равно отношению числовых значений самих векторов:
|
|
|
|
|
(23) |
или в векторной записи |
|
|
|
|
|
|
|
|
|
|
(24) |
где |
|
|
|
|
|
γ s |
= |
e |
|
|
(25) |
m |
|
||||
|
|
|
|
||
— спиновое гиромагнитное отношение, |
γ s |
вдвое |
|||
превышает орбитальное гиромагнитное отношение |
γ l (12) |
||||
(однозначно установлено при определении (22) и (23)). Это позволило выяснить спиновую природу магнитных свойств ферромагнетиков и создать современную теорию ферромагнетизма.
_ _ _ _ _
