1.5.11. Обращение многомерной матрицы

Многомерная матрица В=А^-1называется обратной по отношению к гиперквадратной матрицеА=(р,р), если выполняются следующие соотношения:

А(р,р)В = ВА(р,р) = Е(р,р).(1.20)

Обратная многомерная матрица существует тогда и только тогда, когда определитель исходной гиперквадратной матрицы отличен от нуля. Численное обращение гиперквадратной матрицы может осуществляться путем плоского обращения ее двумерного табличного представления.

Псевдообратной многомерной матрицей В(g,p) = A⁺( g,p)по отно-шению к матрице А(р,g) называется матрица В, удовлетворяющая следующим аналогам условий Мура-Пенроуза [4]:

a) A(p,g)B(g,p)A(p,g) = A(p,g);

б) B(g,p)A(p,g)B(g,p) = B(g,p);

в)[B(g,p)A(p,g)]^T = B(g,p)A(p,g);

г) [A(p,g)B(g,p)]^T = A(p,g)B(g,p).

Псевдообратная матрица всегда существует, и ее табличное представление совпадает с результатом псевдообращения двумерного табличного представления исходной матрицы. При этом выполняется условие – если обратная матрица существует, то она совпадает с псевдообратной: A⁺(p,g) = A^-1(p,g).

Таким образом, общее правило получения обратной матрицы можно записать следующим образом.

1. Обратная матрица строится на основе обращения (псевдообращения) ее табличного представления.

2. Индексы обратной матрицы располагаются так же, как при транспонировании матрицы. Построенная таким образом матрица определяет структуру обратной матрицы, а значения ее элементов устанавливаются по табличному представлению обратной матрицы. Примечание. Многомерные обратные матрицы могут использоваться для представления решения линейных многомерно-матричных уравнений типаА(р,р)Х(р,0)=В(р,0), которое дается соотношенХ(р,0) =А^-1(р,р)В(р,0).

1.5.12. Многомерно-матричное дифференцирование

Многомерно-матричная производная может быть определена следующим образом. Многомерная матрица Z(p+r,q+s), элементы которой являются частными производными элементов многомерно-матричной функцииY(p,q)по элементам многомерно-матричного аргументаX(r,s), называется многомерно-матричной производнойZ(p+r,q+s)= =Y(p,q)/X(r,s). При этом индексы в результирующей матрицеZупорядочиваются по следующему правилу: столбцовые (строчные) индексы матрицыY(p,q) предшествуют столбцовым (строчным) индексам матрицыX(r,s)и расставляются по правилам помечивания индексов:

Z_ijkl=Y_ik/X_jl..

Производная Z(p+r,q+s)образуется путем замены каждого элемента матрицы Y(p,q)блокомY_ik/X(r,s), а каждый такой блок представляет собой матрицу, в которой на месте элементов матрицыX(r,s), стоят соответствующие производные. Проиллюстрируем сказанное на примере дифференцирования обычных матриц.

Y(1,1)={Y_ij}=;

X(1,1)={X_km}=.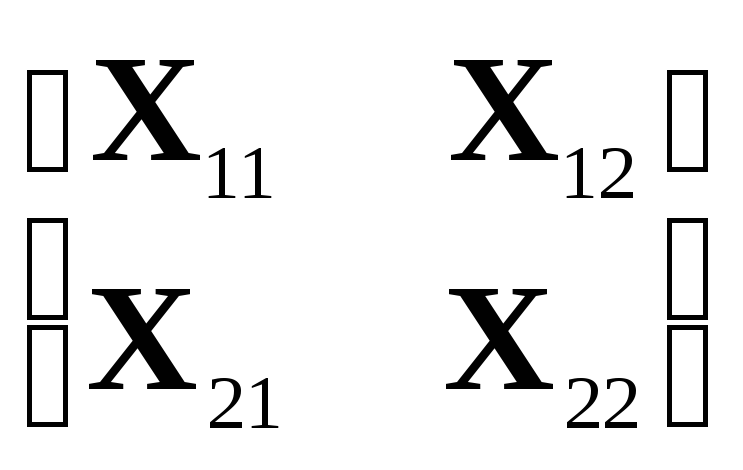

При этом индексы i,kявляются столбцовыми, а индексыj,m- строчными.

Производная Z(2,2)= Y(1,1)/X(1,1)имеет элементыZ_ijkm=Y_ij/X_km и следующее табличное представление:

Z(2,2)= .

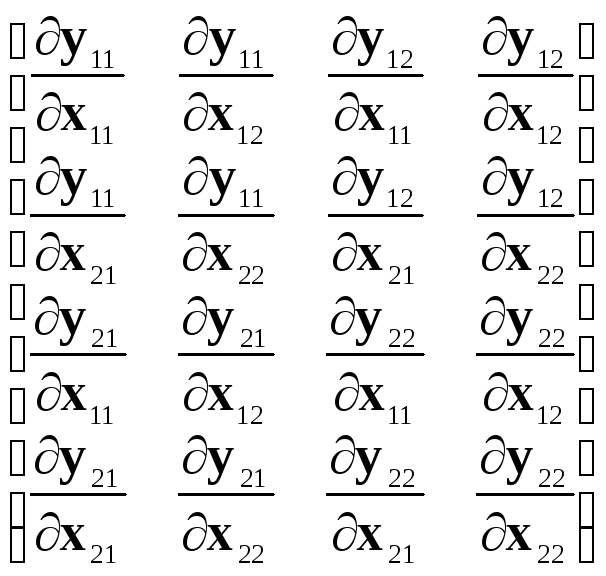1.5.13. Дифференцирование произведения матриц

 (Y*Z)/X=(Y/X)*Z+Y*(Z/X) ;

здесь X,Y,Z- многомерные матрицы.

Таким образом, правила обычного (одномерного) дифференцирования сохраняются и для матричного дифференцирования произведения матриц.