1.5.6. Скоттово (адамарово) произведение многомерных матриц

Кроме свернутого и кронекеровского произведений, иногда приходится рассматривать скоттово (адамарово) произведение многомерных матриц, которое обозначается знаком

и образуется путем поэлементного перемножения соответствующих друг другу элементов матриц одинаковых размерностей, структуры и размеров:

A(p,q) b(p,q)={}.

1.5.7. Векторизация многомерной матрицы

Это операция приведения всех индексов к одной структуре. В соответствии с этим различают два вида векторизации: столбцовую и строчную.

При столбцовой векторизации получается гиперстолбцовая матрица той же размерности. При этом строчные индексы переводят в столбцовые и, сохраняя их внутренний порядок, ставят после столбцовых индексов исходной матрицы. Векторизованную таким образом матрицу удобно отмечать знаком плюс над ее обозначением. Например, В(5,0) = А(3+2,0) есть результат столбцовой векторизации матрицыА(3,2)= {} . Тогда=.

При строчной векторизации получается гиперстрочная матрица исходной размерности. При этом столбцовые индексы переводят в строчные и, сохраняя их внутренний порядок, ставят после строчных индексов исходной матрицы. Векторизованную таким образом матрицу удобно отмечать знаком минус над ее обозначением. Пусть С(0,5)=А(0,2+3)есть результат строчной векторизации матрицыА(3,2)= {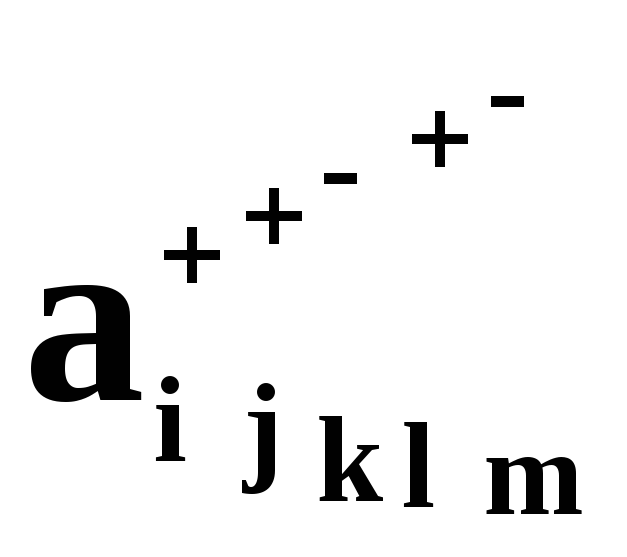} , тогда=.

1.5.8. Девекторизация многомерной матрицы

С помощью этой операции можно восстановить исходную матрицу по ее векторизованному виду. При столбцовой векторизации часть столбцовых индексов (ранее переводившихся из строчных) переводится в строчные и группой ставится впереди непереведенных столбцовых индексов. Далее индексы расставляются по правилу помечивания. Полученная девекторизованная матрица определяет структуру матрицы, а значения ее элементов устанавливаются по исходной векторизованной матрице при одноименных значениях индексов.

При строчной девекторизации часть строчных индексов (ранее переводившихся из столбцовых) переводится в столбцовые и группой ставится впереди непереведенных строчных индексов, и далее индексы расставляются по правилу помечивания. Полученная девекторизованная матрица определяет структуру матрицы, а значения ее элементов устанавливаются по исходной векторизованной матрице при одноименных значениях индексов.

1.5.9. Преобразования структуры векторов

Матрицы E(2,0) иE(0,2) удобно использовать для преобразования структуры векторов.

Z(0,1)*E(2,0)=Z(1,0);

{Z}*{e}={Z};

Z=;

E(0,2)*Z(1,0)=Z(0,1);

{e}*{ Z}={Z};

Z= Z.

1.5.10. Общий алгоритм структурных преобразований многомерных массивов данных

Операции транспонирования, векторизации и девекторизации представляют собой частные случаи структурных преобразований многомерных матриц. Общим свойством этих операций является то, что сами элементы многомерных матриц в результате преобразования не изменяются, а производится их упорядочение. При транспонировании меняются местами строки и столбцы матрицы; при векторизации строки матрицы выстраиваются в столбцы и из них образуется один общий вектор-столбец – гипервектор; девекторизация осуществляет обратную векторизации операцию.

Структура матрицы А(р,g)с размерностью = p+g, как уже отмечалось, определяется количеством индексов столбцового (р) и строчного(g)типа, а также порядком старшинства в пределах группы одного структурного типа. Старшинство индексов подчиняется правилу лексикографического упорядочения, т.е. убывает слева направо. Множество операций структурных преобразований многомерных матриц включает в себя такие действия над матрицами, которые приводят либо к перераспределению индексов матрицы группами столбцового и строчного типа, либо изменяют старшинство индексов, либо производят эти изменения в структуре матрицы одновременно. При этом должны выполняться требования сохранения размерностиматрицы и неизменности значений ее элементов. Для определения числа различных структурных вариантов многомерной матрицы с размерностьюпредставим матрицуА(р,g)в виде А(р,-р). Из последнего выражения видно, что существует+1 различных вариантов отнесения индексов к столбцовому либо строчному типу (показатель размерности р может принимать значения от 0 до). Для конкретного варианта распределения количества индексов столбцового и строчного типа А(р,g) в свою очередь возможны различные размещение и старшинство индексов в группах. Количество различных вариантов такого рода равно числу перестановок из элементов:р_ = ! Таким образом, полное число различных вариантов структур матрицы с размерностьюравно:N= (+1)! = (+1)! Как видно, числоNрастет по факториальной зависимости и уже для обычной «плоской» матрицы(=2)дает 6 структурных вариантов.

Для выполнения структурных преобразований многомерных матриц, как это следует из предыдущего обсуждения, необходимо иметь в распоряжении правила (алгоритмы) для перераспределения индексов матрицы по группам столбцового или строчного типа и изменения их старшинства в пределах группы индексов одного структурного типа. Для решения первой части задачи могут быть использованы алгоритмы векторизации и девекторизации, а смену старшинства индексов можно осуществлять с помощью перестановочных матриц. Рассмотрим общее правило построения перестановочной матрицы, осуществляющей заданную смену старшинства индексов в многомерной матрице, имеющей гиперстолб-цовую структуру А(р,0). Пусть А(р,0) имеет алгебраическое представление:

A(p,q)=

.(1.18)

Тогда любая смена старшинства индексов ₁,₂,..,_росуществляется врезультате левостороннего преобразования с перестановочной матрицей С(р,р):

А^С(р,0) = С(р,р)А(р,0),(1.19)

где А^С(р,0)- матрица А(р,0) с изменением старшинства индексов; С(р,р) – разновидность единичной матрицы, в алгебраическом представлении которой единичные векторы-строки имеют упорядоченность, совпадающую с порядком старшинства индексов в матрицеА(р,0), а единичные векторы-столбцы упорядочены в соответствии со старшинством индексов, требующимся дляА^С(р,0).

Пусть, например, требуется поменять порядок старшинства индексов в матрице (1.18) на обратный, тогда С(р, р) будет иметь алгебраическое представление:

C(p,p)=

.

Действительно, раскрывая произведение матриц в выражении (1.19) с учетом (1.18) и последнего соотношения для С(р₁р), получаем

A^c(p,0)= ,

что соответствует требуемому виду перестановки старшинства индексов.

Аналогичный вид имеют перестановочные матрицы, которые используются в качестве правосторонних преобразователей для смены старшинства индексов в многомерных матрицах гиперстрочной структуры А(0,g)или, в общем случае, для смены старшинства индексов в группе индексов строчного типа в произвольной матрице А(р,g). Таким образом, если речь идет о смене старшинства индексов в матрице А(р,g) без изменения их структурного типа, то можно воспользоваться двухстронним перестановочным преобразованием:

А^с(р,g) = c₁(p,p)A(p,g)c_z(g,g).

Для получения общего алгоритма структурного преобразования многомерной матрицы целесообразно выделить три последовательных этапа трансформации А(р,g):

1) векторизация;

2) смена старшинства индексов в полученной после векторизации матрице гиперстолбцовой (гиперстрочной) структуры;

3) девекторизация, переводящая требуемую часть упорядоченных при выполнении п. 2 индексов в группу строчного (столбцового) типа. Структурная схема преобразования имеет, таким образом, следующий вид: А(р,g)-векторизацияА(p+g,0), смена старшинства индексовА^C (,0), девекторизация, где предполагается, чтоp+g = r+s = .

Рассмотрим пример преобразования трехмерной матрицы А(1,2) с алгебраическим представлением:

A(1,2)=.

Требуется получить матрицу А^с(2,1)со структурой:

A^C(2,1)= .

1. Выполняем векторизацию матрицы А(1,2):

A(3,0)= .

2. Добиваемся требуемого старшинства индексов для нового структурного варианта А^с(2,1)на уровне его алгебраического представленияА^с(3,0):

А^с(3,0)=C(3,3)*A(3,0)={}*{}=.

3. Производим девекторизацию матрицы с переводом индекса jв группу строчных:

A^C(2,1)= .