|
1. Математическая
модель. Погрешность
математической модели связана с ее
приближенным описанием реального
объекта. Например, если при
моделировании экономической системы
не учитывать инфляции, а считать
цены постоянными, трудно рассчитывать
на достоверность результатов.
Погрешность математической модели
называется неустранимой.
Будем в дальнейшем предполагать,
что математическая модель фиксирована
и ее погрешность учитывать не будем.
2. Исходные
данные. Исходные
данные, как правило, содержат
погрешности, так как они либо неточно
измерены, либо являются результатом
решения некоторых вспомогательных
задач. Например, масса снаряда,
производительность оборудования,
предполагаемая цена товара и др. Во
многих физических и технических
задачах погрешность измерений
составляет 1 - 10%. Погрешность исходных
данных так же, как и погрешность
математической модели, считается
неустранимой и в дальнейшем
учитываться не будет.
3.
Метод вычислений. Применяемые
для решения задачи методы как правило
являются приближенными. Например,
заменяют интеграл суммой, функцию
- многочленом, производную - разностью
и т. д. Погрешность метода необходимо
определять для конкретного метода.
Обычно ее можно оценить и
проконтролировать. Следует выбирать
погрешность метода так, чтобы она
была не более, чем на порядок меньше
неустранимой погрешности. Большая
погрешность снижает точность
решения, а меньшая требует значительного
увеличения объема вычислений.
4. Округление
в вычислениях. Погрешность
округления возникает из-за того,
что вычисления производятся с
конечным числом значащих цифр (для
ЭВМ это 10 - 12 знаков). Округление
производят по следующему правилу:
если в старшем из отбрасываемых
разрядов стоит цифра меньше пяти,
то содержимое сохраняемых разрядов
не изменяется; в противном случае
в младший сохраняемый разряд
добавляется единица с тем же знаком,
что и у самого числа. При решении
больших задач производятся миллиарды
вычислений, но так как погрешности
имеют разные знаки, то они частично
взаимокомпенсируются.
Различают
абсолютную
и относительную
погрешности. Пусть а
- точное,
вообще говоря неизвестное числовое
значение некоторой величины, а а*
- известное приближенное значение
этой величины, тогда величину
(а*)
= | а - а*|
называют
абсолютной погрешностью числа
а*,
а величину
(а*)
=
- его относительной
погрешностью.
При сложении и
вычитании складываются абсолютные
погрешности, а при делении и умножении
- относительные погрешности.
1.2 Корректность
Определим вначале
понятие устойчивости
решения.
Решение задачи
y*
называется
устойчивым по исходным данным x*,
если оно зависит от исходных данных
непрерывным образом. Это означает,
что малому изменению исходных данных
соответствует малое изменение
решения. Строго говоря, для любого
> 0 существует =
() > 0
такое, что всякому исходному данному
x*,
удовлетворяющему условию |x
- x*|
< ,
соответствует приближенное решение
y*,
для которого |y
- y*|
< .
Говорят, что
задача поставлена корректно,
если выполнены следующие три условия:
1. Решение
существует при любых допустимых
исходных данных.
2. Это решение
единственно.
3. Это решение
устойчиво по отношению к малым
изменениям исходных данных.
Если хотя бы
одно из этих условий не выполнено,
задача называется некорректной.
Пример 1.1.
Покажем, что
задача вычисления определенного
интеграла I
= корректна. Пусть f*(x)
- приближенно заданная функция и I*
= . Очевидно, приближенное решение
I*
существует
и единственно. Определим абсолютную
погрешность f*
с помощью равенства (f*)
= |f(x)
- f*(x)|.
Так как
(I)
= |I - I*|
= || (b -
a)(f*),
то для любого >
0 неравенство (I)
< будет выполнено, если будет
выполнено условие (f*)
< , где
= /(b
- a).
Таким образом,
решение I*
устойчиво.
Все три условия корректности задачи
выполнены.
Пример 1.2.
Покажем, что
задача вычисления производной u(x)
= f (x)
приближенно заданной функции
некорректна.
Пусть f*(x)
- приближенно заданная на отрезке
[a,
b]
непрерывно дифференцируемая функция
и u*(x)
= (f*(x)).
Определим абсолютные погрешности
следующим образом: (f*)
= |f(x)
- f*(x)|,
(u*)
= |u(x)
- u*(x)|.
Возьмем, например,
f*(x)
= f(x)
+ sin(x/2),
где 0 < <
1. Тогда,
u*(x)
= u(x)
+ -1cos(x/2),
(u*)
= -1,
т. е.
погрешность
задания функции равна ,
а погрешность
производной равна -1.
Таким образом, сколь угодно малой
погрешности задания функции f
может
отвечать сколь угодно большая
погрешность производной f
.
1.3 Вычислительные
методы
Под вычислительными
методами
будем понимать методы, которые
используются в вычислительной
математике для преобразования задач
к виду, удобному для реализации на
ЭВМ. Подробнее с различными классами
вычислительных методов можно
познакомиться, например, в [1]. Мы же
рассмотрим два класса методов,
используемых в нашем курсе.
1. Прямые методы.
Метод решения
задачи называется прямым,
если он позволяет получить решение
после выполнения конечного числа
элементарных операций. Наименование
элементарной операции здесь условно.
Это может быть, например, вычисление
интеграла, решение системы уравнений,
вычисление значений функции и т. д.
Важно то, что ее сложность существенно
меньше, чем сложность основной
задачи. Иногда прямые методы называют
точными,
имея в виду, что при отсутствии
ошибок в исходных данных и при
выполнении элементарных операций
результат будет точным. Однако, при
реализации метода на ЭВМ неизбежны
ошибки округления и, как следствие,
наличие вычислительной погрешности.
2. Итерационные
методы. Суть
итерационных
методов
состоит в построении последовательных
приближений к решению задачи. Вначале
выбирают одно или несколько начальных
приближений, а затем последовательно,
используя найденные ранее приближения
и однотипную процедуру расчета,
строят новые приближения. В результате
такого итерационного
процесса
можно теоретически построить
бесконечную последовательность
приближений к решению. Если эта
последовательность сходится (что
бывает не всегда), то говорят, что
итерационный метод сходится.
Отдельный шаг итерационного процесса
называется итерацией.
Практически
вычисления не могут продолжаться
бесконечно долго. Поэтому необходимо
выбрать критерий
окончания итерационного процесса.
Критерий окончания связан с требуемой
точностью вычислений, а именно:
вычисления заканчиваются, когда
погрешность приближения не превышает
заданной величины.
Оценки погрешности
приближения, полученные до вычислений,
называют априорными
оценками (от
лат. apriori - "до опыта"), а
соответствующие оценки, полученные
в ходе вычислений называют
апостериорными
оценками (от
лат. aposteriori - "после опыта").
Важной
характеристикой итерационных
методов является скорость
сходимости
метода. Говорят, что метод имеет
p-ый
порядок сходимости если
|xn+1
- x*|
= C|xn
- x*|p,
где xn
и xn+1
- последовательные приближения,
полученные в ходе итерационного
процесса вычислений, x*
- точное
решение, C - константа, не зависящая
от n.
Говорят, что метод сходится со
скоростью геометрической прогрессии
со знаменателем q < 1, если для всех
n
справедлива оценка:
|xn
- x*|
Cqn.
Итерационный
процесс называется одношаговым,
если для вычисления очередного
приближения xn+1
используется т
|
Вычислительная
математика отличается от других
математических дисциплин следующими
специфическими особенностями.
Вычислительная
математика обычно имеет дело не
с непрерывными, а с дискретными
объектами, которыми приближаются
непрерывные. Так, вместо отрезка
прямой часто рассматривается
система точек
 (это
введенная на отрезке СЕТКА), вместо
непрерывной функцииf(х)
— табличная функция (это
введенная на отрезке СЕТКА), вместо
непрерывной функцииf(х)
— табличная функция
 ,
вместо первой производной — ее
разностная аппроксимация, например, ,
вместо первой производной — ее
разностная аппроксимация, например,
   Такие
замены, естественно, порождают
погрешности метода.
Погрешности
метода являются неустранимыми
погрешностями.
Рассмотрим
вопрос, какую неустранимую
погрешность вносит замена
непрерывной функции ее ПРОЕКЦИЕЙ
(ОГРАНИЧЕНИЕМ) на сетку.
Примечание.
Переход от непрерывной функции к
ее сеточному аналогу достигается
применением оператора ограничения,
или проектора. Такие операторы
могут быть построены разными
способами. Простейший способ
построения проектора – взять
значения функции в точках сетки.
Конечно, применение оператора
проектора приводит к появлению
неустранимых погрешностей, так
как часть информации о функции
теряется.
Здесь и далее мы
будем считать, что функция, проекцией
которой на сетку мы пользуемся,
достаточно гладкая и нужное число
раз непрерывно дифференцируемая.
Какое число непрерывных производных
нам потребуется, каждый раз будем
оговаривать специально.
Пример.
Оценить неустранимую погрешность,
возникающую при проекции на сетку
дважды непрерывно дифференцируемой
функции Такие
замены, естественно, порождают
погрешности метода.
Погрешности
метода являются неустранимыми
погрешностями.
Рассмотрим
вопрос, какую неустранимую
погрешность вносит замена
непрерывной функции ее ПРОЕКЦИЕЙ
(ОГРАНИЧЕНИЕМ) на сетку.
Примечание.
Переход от непрерывной функции к
ее сеточному аналогу достигается
применением оператора ограничения,
или проектора. Такие операторы
могут быть построены разными
способами. Простейший способ
построения проектора – взять
значения функции в точках сетки.
Конечно, применение оператора
проектора приводит к появлению
неустранимых погрешностей, так
как часть информации о функции
теряется.
Здесь и далее мы
будем считать, что функция, проекцией
которой на сетку мы пользуемся,
достаточно гладкая и нужное число
раз непрерывно дифференцируемая.
Какое число непрерывных производных
нам потребуется, каждый раз будем
оговаривать специально.
Пример.
Оценить неустранимую погрешность,
возникающую при проекции на сетку
дважды непрерывно дифференцируемой
функции Считаем,
что введенная на отрезке [0,1] сетка
равномерная,
т.е. Считаем,
что введенная на отрезке [0,1] сетка
равномерная,
т.е.
 Решение.
Очевидно, что Решение.
Очевидно, что принадлежит
рассматриваемому классу. Сеточная
функция принадлежит
рассматриваемому классу. Сеточная
функция есть
проекция на сетку. Рассмотрим
функции есть
проекция на сетку. Рассмотрим
функции и и Обе
этих функции принадлежат
рассматриваемому классу функций,
а применение оператора проекции
дает в результате Обе
этих функции принадлежат
рассматриваемому классу функций,
а применение оператора проекции
дает в результате .
Тем не менее, между узлами скетки
данные функции могут отличаться
на .
Тем не менее, между узлами скетки
данные функции могут отличаться
на
В машинных
вычислениях используются числа
с конечным количеством знаков
после запятой (конечные приближения
действительных чисел) из-за
конечности длины мантиссы при
представлении действительного
числа в памяти ЭВМ. Другими словами,
в вычислениях присутствует
машинная погрешность (округления)
 .
Это приводит к вычислительным
эффектам, неизвестным, например,
в классической теории обыкновенных
дифференциальных уравнений,
уравнений математической физики
или в математическом анализе. .
Это приводит к вычислительным
эффектам, неизвестным, например,
в классической теории обыкновенных
дифференциальных уравнений,
уравнений математической физики
или в математическом анализе.
В вычислительной
практике большое значение имеет
обусловленность
задачи,
т. е. чувствительность ее решения
к малым изменениям входных данных.
В отличие
от «классической» математики
выбор вычислительного алгоритма
влияет на результаты вычислений.
Существенная
черта численного метода —
экономичность
вычислительного алгоритма, т. е.
минимизация числа элементарных
операций при выполнении его на
ЭВМ.
Погрешности
при численном решении задач
делятся на две категории —
неустранимые и устранимые. К
первым относят погрешности,
связанные с построением
математической модели объекта и
приближенным заданием входных
данных, ко вторым — погрешности
метода решения задачи и ошибки
округления, которые являются
источниками малых возмущений,
вносимых в решение задачи.
Элементы
теории погрешностей
Определение.
Пусть u
и
 —
точное и приближенное значение
некоторой величины соответственно.
Тогдаабсолютной
погрешностью
приближения u*
называется величина —
точное и приближенное значение
некоторой величины соответственно.
Тогдаабсолютной
погрешностью
приближения u*
называется величина
 ,
удовлетворяющая неравенству ,
удовлетворяющая неравенству Определение.
Относительной
погрешностью
называется величина Определение.
Относительной
погрешностью
называется величина
 ,
удовлетворяющая неравенству ,
удовлетворяющая неравенству Обычно
используется запись Обычно
используется запись Определение.
Пусть искомая величина u
является функцией параметров Определение.
Пусть искомая величина u
является функцией параметров
 u*
—
приближенное значение u.
Тогда предельной абсолютной
погрешностью называется
величина u*
—
приближенное значение u.
Тогда предельной абсолютной
погрешностью называется
величина
 Предельной
относительной погрешностью
называется величина Предельной
относительной погрешностью
называется величина
 Пусть Пусть  —
приближенное значение —
приближенное значение Предполагаем,
чтоu
— непрерывно дифференцируемая
функция своих аргументов. Тогда,
по формуле Лагранжа, Предполагаем,
чтоu
— непрерывно дифференцируемая
функция своих аргументов. Тогда,
по формуле Лагранжа,
 где где  Отсюда Отсюда где где Можно
показать, что при малых Можно
показать, что при малых  это
оценка не может быть существенно
улучшена. На практике иногда
пользуются грубой (линейной)
оценкой это
оценка не может быть существенно
улучшена. На практике иногда
пользуются грубой (линейной)
оценкой где где Несложно
показать, чтоа) Несложно
показать, чтоа)
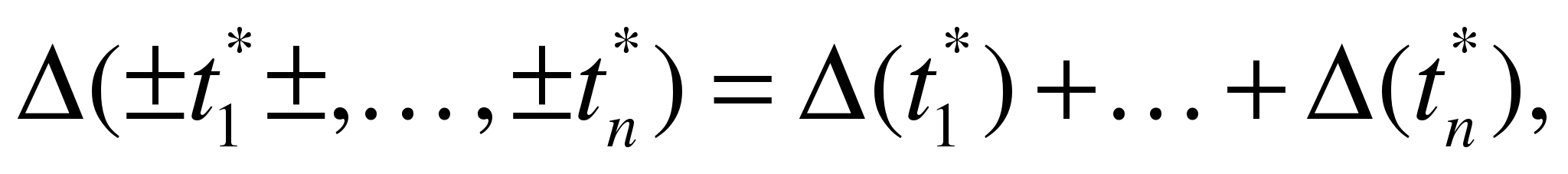 предельная
погрешность суммы или разности
равна сумме или разности предельных
погрешностей.в)
Предельная относительная погрешность
произведения или частного
приближенного равна сумме предельных
относительных погрешностей предельная
погрешность суммы или разности
равна сумме или разности предельных
погрешностей.в)
Предельная относительная погрешность
произведения или частного
приближенного равна сумме предельных
относительных погрешностей
 Погрешность
метода
Оценим
погрешность при вычислении первой
производной при помощи соотношения Погрешность
метода
Оценим
погрешность при вычислении первой
производной при помощи соотношения
 : : гдеO(h)
есть погрешность метода. В данном
случае под погрешностью метода
понимается абсолютная величина
разности гдеO(h)
есть погрешность метода. В данном
случае под погрешностью метода
понимается абсолютная величина
разности
 ,
которая составляетO(h)
(более точно ,
которая составляетO(h)
(более точно
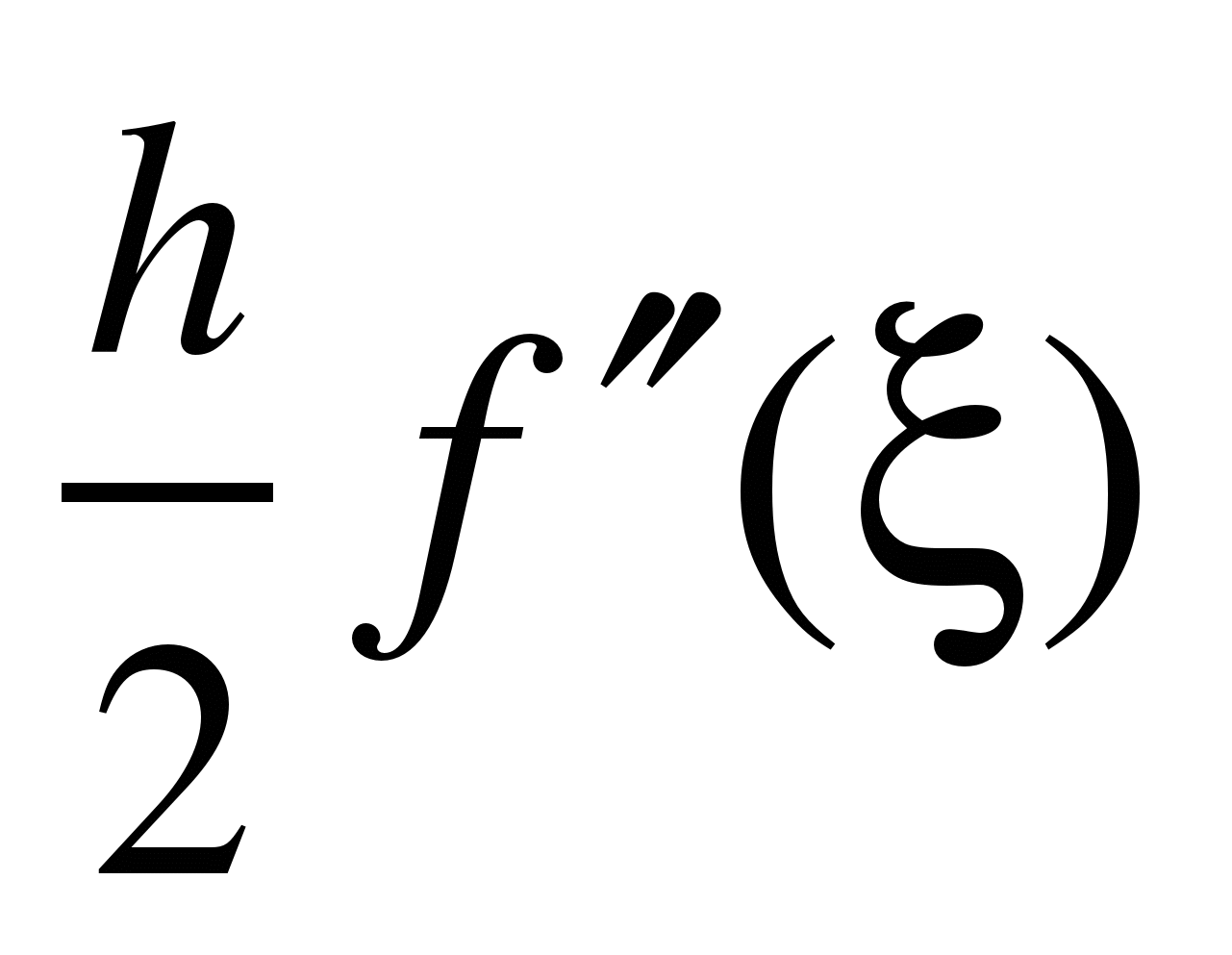 ,
где ,
где ).
Если
же взять другой метод вычисления
производной ).
Если
же взять другой метод вычисления
производной ,
то получим, что его погрешность
составляетO(h2),
это оказывается существенным при
малых h.
Однако уменьшать h
до бесконечности не имеет смысла,
что видно из следующего примера.
Реальная погрешность при вычислении
первой производной будет ,
то получим, что его погрешность
составляетO(h2),
это оказывается существенным при
малых h.
Однако уменьшать h
до бесконечности не имеет смысла,
что видно из следующего примера.
Реальная погрешность при вычислении
первой производной будет
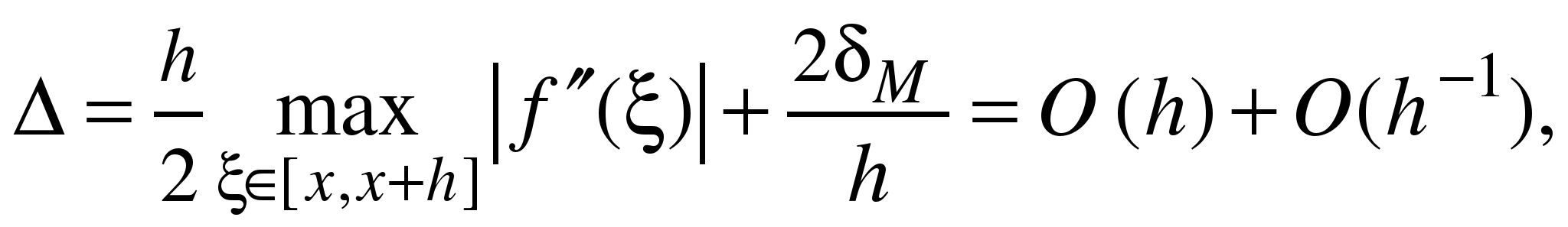 поскольку
погрешность за счет машинного
округления составит поскольку
погрешность за счет машинного
округления составит .
В
этом случае можно найти оптимальный
шагh.
Будем
считать полную погрешность в
вычислении производной Δ функцией
шага h.
Отыщем минимум этой функции.
Приравняв производную .
В
этом случае можно найти оптимальный
шагh.
Будем
считать полную погрешность в
вычислении производной Δ функцией
шага h.
Отыщем минимум этой функции.
Приравняв производную
 к
нулю, получим оптимальный шаг
численного дифференцирования к
нулю, получим оптимальный шаг
численного дифференцирования Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти из-за
возрастания вклада ошибок
округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения производной
подробнее.
Пусть задана таблица
значений xi.
В дальнейшем совокупность точек
на отрезке, котором проводятся
вычисления, иногда будут называться
сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная, и
расстояние между узлами равно Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти из-за
возрастания вклада ошибок
округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения производной
подробнее.
Пусть задана таблица
значений xi.
В дальнейшем совокупность точек
на отрезке, котором проводятся
вычисления, иногда будут называться
сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная, и
расстояние между узлами равно
 —шагу
сетки.
Пусть узлы сетки пронумерованы в
порядке возрастания, т.е. —шагу
сетки.
Пусть узлы сетки пронумерованы в
порядке возрастания, т.е.
  , ,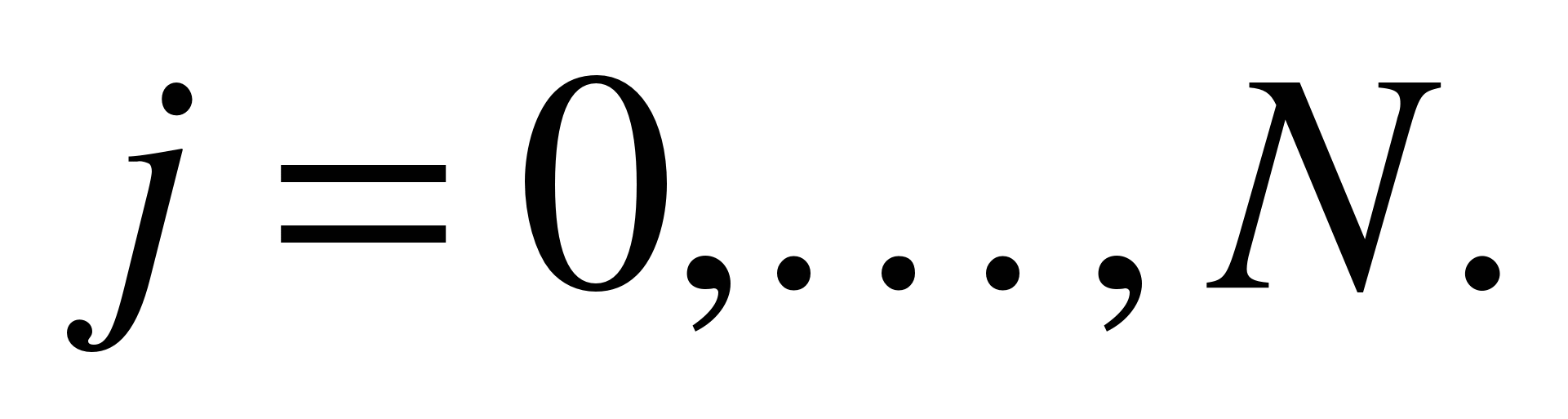 Пусть Пусть —
функция, определенная в узлах
сетки. Такие функции будут называться
табличными, или сеточными функциями.
Считаем, кроме того, что рассматриваемая
сеточная функция есть проекция
(или ограничение) на сетку некоторой
гладкой нужное число раз непрерывно
дифференцируемой функцииf(x).
По определению производной —
функция, определенная в узлах
сетки. Такие функции будут называться
табличными, или сеточными функциями.
Считаем, кроме того, что рассматриваемая
сеточная функция есть проекция
(или ограничение) на сетку некоторой
гладкой нужное число раз непрерывно
дифференцируемой функцииf(x).
По определению производной
 тогда,
если шаг сетки достаточно мал, по
аналогии можно написать формулу
в конечных разностях, дающую
приближенное значение производной
сеточной функции: тогда,
если шаг сетки достаточно мал, по
аналогии можно написать формулу
в конечных разностях, дающую
приближенное значение производной
сеточной функции: (1.1)
Если
параметр (1.1)
Если
параметр достаточно
мал, то можно считать полученное
значение производной достаточно
точным. Погрешность формулы (1.1)
оценена в пункте 1.4. Как показано
выше, при уменьшении шага сеткиh
ошибка будет уменьшаться, но при
некотором значении достаточно
мал, то можно считать полученное
значение производной достаточно
точным. Погрешность формулы (1.1)
оценена в пункте 1.4. Как показано
выше, при уменьшении шага сеткиh
ошибка будет уменьшаться, но при
некотором значении
 ошибка
может возрасти до бесконечности.
При оценке погрешности метода
обычно считается, что все вычисления
были точными. Но существует ошибка
округления. При оценке ее большую
роль играет машинный ε — мера
относительной погрешности машинного
округления, возникающей из-за
конечной разрядности мантиссы
при работе с числами в формате с
плавающей точкой. Напомним, что
по определению машинным ε называют
наибольшее из чисел, для которых
в рамках используемой системы
вычислений, выполнено 1 + ε = 1.
Тогда абсолютная погрешность при
вычислении значения функции (или
представлении табличной функции)
есть ошибка
может возрасти до бесконечности.
При оценке погрешности метода
обычно считается, что все вычисления
были точными. Но существует ошибка
округления. При оценке ее большую
роль играет машинный ε — мера
относительной погрешности машинного
округления, возникающей из-за
конечной разрядности мантиссы
при работе с числами в формате с
плавающей точкой. Напомним, что
по определению машинным ε называют
наибольшее из чисел, для которых
в рамках используемой системы
вычислений, выполнено 1 + ε = 1.
Тогда абсолютная погрешность при
вычислении значения функции (или
представлении табличной функции)
есть Максимальный
вклад погрешностей округления
при вычислении производной по
формуле (1.1) будет Максимальный
вклад погрешностей округления
при вычислении производной по
формуле (1.1) будет тогда,
когда члены в знаменателе (1.1) имеют
ошибки разных знаков.
Пусть тогда,
когда члены в знаменателе (1.1) имеют
ошибки разных знаков.
Пусть максимум
ищется на отрезке, на котором
вычисляются значения производных.
Тогда суммарная ошибка, состоящая
из погрешности метода и погрешности
округления, есть максимум
ищется на отрезке, на котором
вычисляются значения производных.
Тогда суммарная ошибка, состоящая
из погрешности метода и погрешности
округления, есть  Для
вычисления оптимального шага
численного дифференцирования
найдем минимум суммарной ошибки,
как функции шага сетки Для
вычисления оптимального шага
численного дифференцирования
найдем минимум суммарной ошибки,
как функции шага сетки откуда откуда Если
требуется повысить точность
вычисления производных, необходимо
воспользоваться формулами, имеющими
меньшие погрешности метода. Так,
из курсов математического анализа
известно, что Если
требуется повысить точность
вычисления производных, необходимо
воспользоваться формулами, имеющими
меньшие погрешности метода. Так,
из курсов математического анализа
известно, что По
аналогии напишем конечно-разностную
формулу По
аналогии напишем конечно-разностную
формулу (1.2)
(1.2)
— формула с центральной разностью.
Исследуем ее на аппроксимацию,
т.е. оценим погрешность метода.
Предположим, что функция, которую
спроектировали на сетку, трижды
непрерывно дифференцируема,
тогда (1.2)
(1.2)
— формула с центральной разностью.
Исследуем ее на аппроксимацию,
т.е. оценим погрешность метода.
Предположим, что функция, которую
спроектировали на сетку, трижды
непрерывно дифференцируема,
тогда 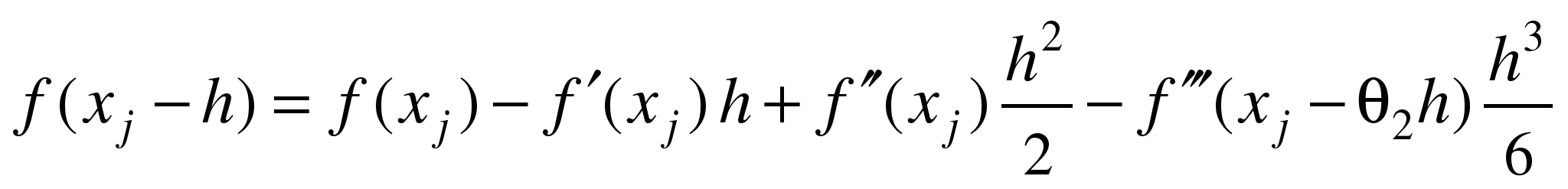 Погрешность
метода определяется 3-й производной
функции. Введем Погрешность
метода определяется 3-й производной
функции. Введем тогда
суммарная погрешность при вычислении
по формуле с центральной разностью
есть тогда
суммарная погрешность при вычислении
по формуле с центральной разностью
есть для
вычисления оптимального шага,
находя минимум погрешности, как
функции шага сетки, имеем для
вычисления оптимального шага,
находя минимум погрешности, как
функции шага сетки, имеем откуда откуда Для
более точного вычисления производной,
необходимо использовать, разложение
более высокого порядка, шаг Для
более точного вычисления производной,
необходимо использовать, разложение
более высокого порядка, шаг будет
увеличиваться.
Формула (1.1) —
двухточечная, (1.2) — трехточечная:
при вычислении производной
используются точки (узлы) будет
увеличиваться.
Формула (1.1) —
двухточечная, (1.2) — трехточечная:
при вычислении производной
используются точки (узлы) (узел
входит с нулевым коэффициентом), (узел
входит с нулевым коэффициентом), , , —
совокупность узлов, участвующих
в каждом вычислении производной,
в дальнейшем будем иногда называтьсеточным
шаблоном.
Введем
на рассматриваемом отрезке шаблон
из нескольких точек.
Считаем,
что сетка равномерная — шаг сетки
постоянный, расстояния между
любыми двумя соседними узлами
равны. Используем для вычисления
значения первой производной
следующую приближенную
(конечноразностную)
формулу: —
совокупность узлов, участвующих
в каждом вычислении производной,
в дальнейшем будем иногда называтьсеточным
шаблоном.
Введем
на рассматриваемом отрезке шаблон
из нескольких точек.
Считаем,
что сетка равномерная — шаг сетки
постоянный, расстояния между
любыми двумя соседними узлами
равны. Используем для вычисления
значения первой производной
следующую приближенную
(конечноразностную)
формулу:
 (1.3)
шаблон
включаетl
точек слева от рассматриваемой
точки xj
и m
справа. Коэффициенты α —
неопределенные
коэффициенты.
Формула дифференцирования может
быть и односторонней
— либо l,
либо
m могут
равняться нулю. В первом случае
иногда называют (на наш взгляд, не
слишком удачно) такую приближенную
формулу формулой дифференцирования
вперед, во втором — формулой
дифференцирования назад. Потребуем,
чтобы (1.3) приближала первую
производную с точностью (1.3)
шаблон
включаетl
точек слева от рассматриваемой
точки xj
и m
справа. Коэффициенты α —
неопределенные
коэффициенты.
Формула дифференцирования может
быть и односторонней
— либо l,
либо
m могут
равняться нулю. В первом случае
иногда называют (на наш взгляд, не
слишком удачно) такую приближенную
формулу формулой дифференцирования
вперед, во втором — формулой
дифференцирования назад. Потребуем,
чтобы (1.3) приближала первую
производную с точностью
 Используем
разложения в ряд Тейлора в
окрестности точкиxj.
Подставляя их в (1.3),
получим Используем
разложения в ряд Тейлора в
окрестности точкиxj.
Подставляя их в (1.3),
получим
  Потребуем
выполнение условий: Потребуем
выполнение условий:   …, …, …
(1.4)
Получаем систему линейных
алгебраических уравнений для
неопределенных коэффициентов α
(1.4). Матрица этой системы
есть …
(1.4)
Получаем систему линейных
алгебраических уравнений для
неопределенных коэффициентов α
(1.4). Матрица этой системы
есть Вектор
правых частей (0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не равен
нулю. Тогда существует единственный
набор коэффициентов α, который
позволяет найти на шаблоне из
(1 + l + m)
точек значение первой производной
с точностью Вектор
правых частей (0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не равен
нулю. Тогда существует единственный
набор коэффициентов α, который
позволяет найти на шаблоне из
(1 + l + m)
точек значение первой производной
с точностью
 Для
нахождения второй производной
можно использовать ту же самую
формулу (1.3) с небольшой
модификацией Для
нахождения второй производной
можно использовать ту же самую
формулу (1.3) с небольшой
модификацией только
теперь только
теперь  Очевидно,
что и данная система уравнений
для нахождения неопределенных
коэффициентов имеет единственное
решение. Для получения с той же
точностью приближенных значений
производных до порядкаl + m
включительно
с точностью Очевидно,
что и данная система уравнений
для нахождения неопределенных
коэффициентов имеет единственное
решение. Для получения с той же
точностью приближенных значений
производных до порядкаl + m
включительно
с точностью
 модификации
формулы (1.3) и условий (1.4) очевидны,
набор неопределенных коэффициентов
находится единственным образом.
Таким
образом, доказано следующее
утверждение. На сеточном шаблоне,
включающем в себяN + 1
точку, с помощью метода неопределенных
коэффициентов всегда можно
построить единственную формулу
для вычисления производной от
первого до N
порядка включительно с точностью модификации
формулы (1.3) и условий (1.4) очевидны,
набор неопределенных коэффициентов
находится единственным образом.
Таким
образом, доказано следующее
утверждение. На сеточном шаблоне,
включающем в себяN + 1
точку, с помощью метода неопределенных
коэффициентов всегда можно
построить единственную формулу
для вычисления производной от
первого до N
порядка включительно с точностью
 .
Утверждение
доказано для равномерной сетки,
но на случай произвольных расстояний
между сеточными узлами обобщение
проводится легко.
Так как на
практике вычисления проводятся
с конечной длиной мантиссы, то
получить нулевую ошибку невозможно. .
Утверждение
доказано для равномерной сетки,
но на случай произвольных расстояний
между сеточными узлами обобщение
проводится легко.
Так как на
практике вычисления проводятся
с конечной длиной мантиссы, то
получить нулевую ошибку невозможно. |
|
|
|
|
|
|
|
|
|
|
|
t;
Таким
образом, решение I*
устойчиво.
Все три условия корректности
задачи выполнены. Пример
1.2. Покажем,
что задача вычисления производной
u(x)
= f (x)
приближенно заданной функции
некорректна. Пусть
f*(x)
- приближенно заданная на
отрезке [a,
b]
непрерывно дифференцируемая
функция и u*(x)
= (f*(x)).
Определим абсолютные погрешности
следующим образом: (f*)
= |f(x)
- f*(x)|,
(u*)
= |u(x)
- u*(x)|.
Возьмем,
например, f*(x)
= f(x)
+ sin(x/2),
где
0 < <
1.
Тогда, u*(x)
= u(x)
+ -1cos(x/2),
(u*)
= -1,
т.
е.
погрешность
задания функции равна ,
а
погрешность производной равна
-1.
Таким образом, сколь угодно
малой погрешности задания
функции f
может
отвечать сколь угодно большая
погрешность производной f
. 1.3
Вычислительные методы Под
вычислительными
методами
будем понимать методы, которые
используются в вычислительной
математике для преобразования
задач к виду, удобному для
реализации на ЭВМ. Подробнее
с различными классами
вычислительных методов можно
познакомиться, например, в [1].
Мы же рассмотрим два класса
методов, используемых в нашем
курсе. 1.
Прямые методы. Метод
решения задачи называется
прямым,
если он позволяет получить
решение после выполнения
конечного числа элементарных
операций. Наименование
элементарной операции здесь
условно. Это может быть, например,
вычисление интеграла, решение
системы уравнений, вычисление
значений функции и т. д. Важно
то, что ее сложность существенно
меньше, чем сложность основной
задачи. Иногда прямые методы
называют точными,
имея в виду, что при отсутствии
ошибок в исходных данных и при
выполнении элементарных
операций результат будет
точным. Однако, при реализации
метода на ЭВМ неизбежны ошибки
округления и, как следствие,
наличие вычислительной
погрешности. 2.
Итерационные методы. Суть
итерационных
методов
состоит в построении
последовательных приближений
к решению задачи. Вначале
выбирают одно или несколько
начальных приближений, а затем
последовательно, используя
найденные ранее приближения
и однотипную процедуру расчета,
строят новые приближения. В
результате такого итерационного
процесса
можно теоретически построить
бесконечную последовательность
приближений к решению. Если
эта последовательность сходится
(что бывает не всегда), то
говорят, что итерационный метод
сходится. Отдельный шаг
итерационного процесса
называется итерацией.
Практически
вычисления не могут продолжаться
бесконечно долго. Поэтому
необходимо выбрать критерий
окончания итерационного
процесса.
Критерий окончания связан с
требуемой точностью вычислений,
а именно: вычисления заканчиваются,
когда погрешность приближения
не превышает заданной величины. Оценки
погрешности приближения,
полученные до вычислений,
называют априорными
оценками (от
лат. apriori - "до опыта"), а
соответствующие оценки,
полученные в ходе вычислений
называют апостериорными
оценками (от
лат. aposteriori - "после опыта"). Важной
характеристикой итерационных
методов является скорость
сходимости
метода. Говорят, что метод имеет
p-ый
порядок сходимости если |xn+1
- x*|
= C|xn
- x*|p,
где
xn
и xn+1
- последовательные приближения,
полученные в ходе итерационного
процесса вычислений, x*
-
точное решение, C - константа,
не зависящая от n.
Говорят, что метод сходится со
скоростью геометрической
прогрессии со знаменателем q
< 1, если для всех n
справедлива оценка: |xn
- x*|
Cqn.
Итерационный
процесс называется одношаговым,
если для вычисления очередного
приближения xn+1
используется только одно
предыдущее приближение xn
и k
-шаговым, если
для вычисления xn+1
используются k
предыдущих приближений xn-k+1,
xn-k+2,
…, xn.
|
Лекция
1
Вычислительная математика
отличается от других
математических дисциплин
следующими специфическими
особенностями.
Вычислительная
математика обычно имеет дело
не с непрерывными, а с
дискретными объектами,
которыми приближаются
непрерывные. Так, вместо
отрезка прямой часто
рассматривается система
точек
 (это
введенная на отрезке СЕТКА),
вместо непрерывной функцииf(х)
— табличная функция (это
введенная на отрезке СЕТКА),
вместо непрерывной функцииf(х)
— табличная функция
 ,
вместо первой производной
— ее разностная аппроксимация,
например, ,
вместо первой производной
— ее разностная аппроксимация,
например,
   Такие
замены, естественно, порождают
погрешности метода.
Погрешности
метода являются неустранимыми
погрешностями.
Рассмотрим
вопрос, какую неустранимую
погрешность вносит замена
непрерывной функции ее
ПРОЕКЦИЕЙ (ОГРАНИЧЕНИЕМ) на
сетку.
Примечание. Переход
от непрерывной функции к ее
сеточному аналогу достигается
применением оператора
ограничения, или проектора.
Такие операторы могут быть
построены разными способами.
Простейший способ построения
проектора – взять значения
функции в точках сетки.
Конечно, применение оператора
проектора приводит к появлению
неустранимых погрешностей,
так как часть информации о
функции теряется.
Здесь
и далее мы будем считать, что
функция, проекцией которой
на сетку мы пользуемся,
достаточно гладкая и нужное
число раз непрерывно
дифференцируемая. Какое число
непрерывных производных нам
потребуется, каждый раз будем
оговаривать специально.
Пример.
Оценить неустранимую
погрешность, возникающую при
проекции на сетку дважды
непрерывно дифференцируемой
функции Такие
замены, естественно, порождают
погрешности метода.
Погрешности
метода являются неустранимыми
погрешностями.
Рассмотрим
вопрос, какую неустранимую
погрешность вносит замена
непрерывной функции ее
ПРОЕКЦИЕЙ (ОГРАНИЧЕНИЕМ) на
сетку.
Примечание. Переход
от непрерывной функции к ее
сеточному аналогу достигается
применением оператора
ограничения, или проектора.
Такие операторы могут быть
построены разными способами.
Простейший способ построения
проектора – взять значения
функции в точках сетки.
Конечно, применение оператора
проектора приводит к появлению
неустранимых погрешностей,
так как часть информации о
функции теряется.
Здесь
и далее мы будем считать, что
функция, проекцией которой
на сетку мы пользуемся,
достаточно гладкая и нужное
число раз непрерывно
дифференцируемая. Какое число
непрерывных производных нам
потребуется, каждый раз будем
оговаривать специально.
Пример.
Оценить неустранимую
погрешность, возникающую при
проекции на сетку дважды
непрерывно дифференцируемой
функции Считаем,
что введенная на отрезке
[0,1] сетка
равномерная,
т.е. Считаем,
что введенная на отрезке
[0,1] сетка
равномерная,
т.е.
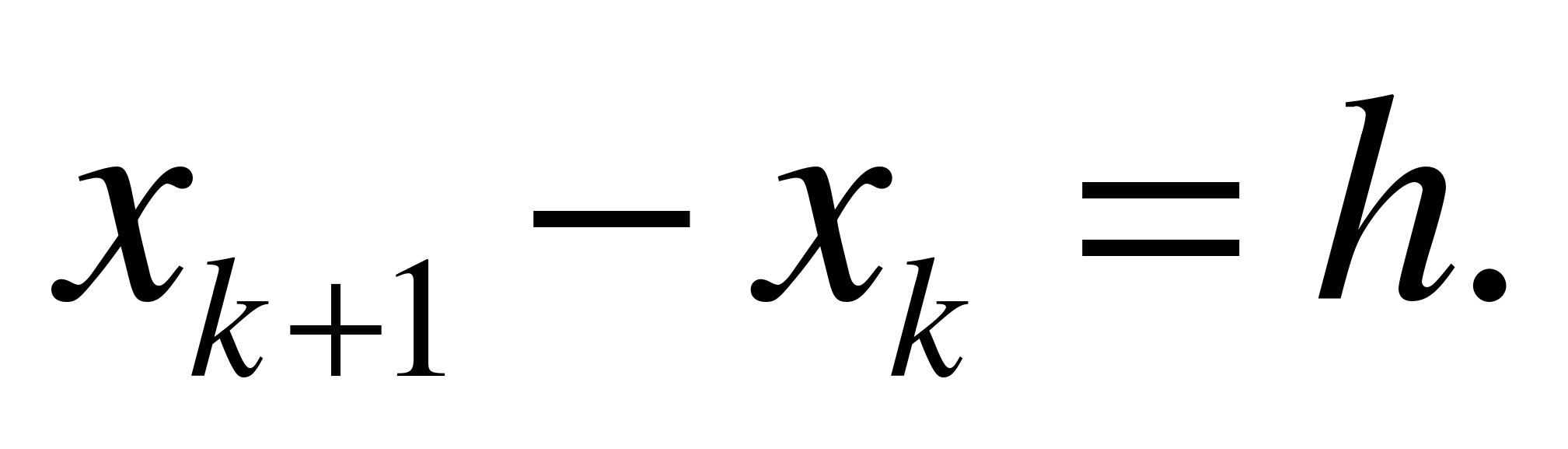 Решение.
Очевидно, что Решение.
Очевидно, что принадлежит
рассматриваемому классу.
Сеточная функция принадлежит
рассматриваемому классу.
Сеточная функция есть
проекция на сетку. Рассмотрим
функции есть
проекция на сетку. Рассмотрим
функции и и Обе
этих функции принадлежат
рассматриваемому классу
функций, а применение оператора
проекции дает в результате Обе
этих функции принадлежат
рассматриваемому классу
функций, а применение оператора
проекции дает в результате .
Тем не менее, между узлами
скетки данные функции могут
отличаться на .
Тем не менее, между узлами
скетки данные функции могут
отличаться на
В
машинных вычислениях
используются числа с конечным
количеством знаков после
запятой (конечные приближения
действительных чисел) из-за
конечности длины мантиссы
при представлении действительного
числа в памяти ЭВМ. Другими
словами, в вычислениях
присутствует машинная
погрешность (округления)
 .
Это приводит к вычислительным
эффектам, неизвестным,
например, в классической
теории обыкновенных
дифференциальных уравнений,
уравнений математической
физики или в математическом
анализе. .
Это приводит к вычислительным
эффектам, неизвестным,
например, в классической
теории обыкновенных
дифференциальных уравнений,
уравнений математической
физики или в математическом
анализе.
В
вычислительной практике
большое значение имеет
обусловленность
задачи,
т. е. чувствительность ее
решения к малым изменениям
входных данных.
В
отличие от «классической»
математики выбор вычислительного
алгоритма влияет на результаты
вычислений.
Существенная
черта численного метода —
экономичность
вычислительного алгоритма,
т. е. минимизация числа
элементарных операций при
выполнении его на ЭВМ.
Погрешности
при численном решении задач
делятся на две категории —
неустранимые и устранимые.
К первым относят погрешности,
связанные с построением
математической модели объекта
и приближенным заданием
входных данных, ко вторым —
погрешности метода решения
задачи и ошибки округления,
которые являются источниками
малых возмущений, вносимых
в решение задачи.
Элементы
теории погрешностей
Определение.
Пусть u
и
 —
точное и приближенное значение
некоторой величины
соответственно. Тогдаабсолютной
погрешностью
приближения u*
называется величина —
точное и приближенное значение
некоторой величины
соответственно. Тогдаабсолютной
погрешностью
приближения u*
называется величина
 ,
удовлетворяющая
неравенству ,
удовлетворяющая
неравенству Определение.
Относительной
погрешностью
называется величина Определение.
Относительной
погрешностью
называется величина
 ,
удовлетворяющая
неравенству ,
удовлетворяющая
неравенству Обычно
используется запись Обычно
используется запись Определение.
Пусть искомая величина u
является функцией параметров Определение.
Пусть искомая величина u
является функцией параметров
 u*
—
приближенное значение u.
Тогда предельной абсолютной
погрешностью называется
величина u*
—
приближенное значение u.
Тогда предельной абсолютной
погрешностью называется
величина
 Предельной
относительной погрешностью
называется величина Предельной
относительной погрешностью
называется величина
 Пусть Пусть  —
приближенное значение —
приближенное значение Предполагаем,
чтоu
— непрерывно дифференцируемая
функция своих аргументов.
Тогда, по формуле Лагранжа, Предполагаем,
чтоu
— непрерывно дифференцируемая
функция своих аргументов.
Тогда, по формуле Лагранжа,
 где где  Отсюда Отсюда где где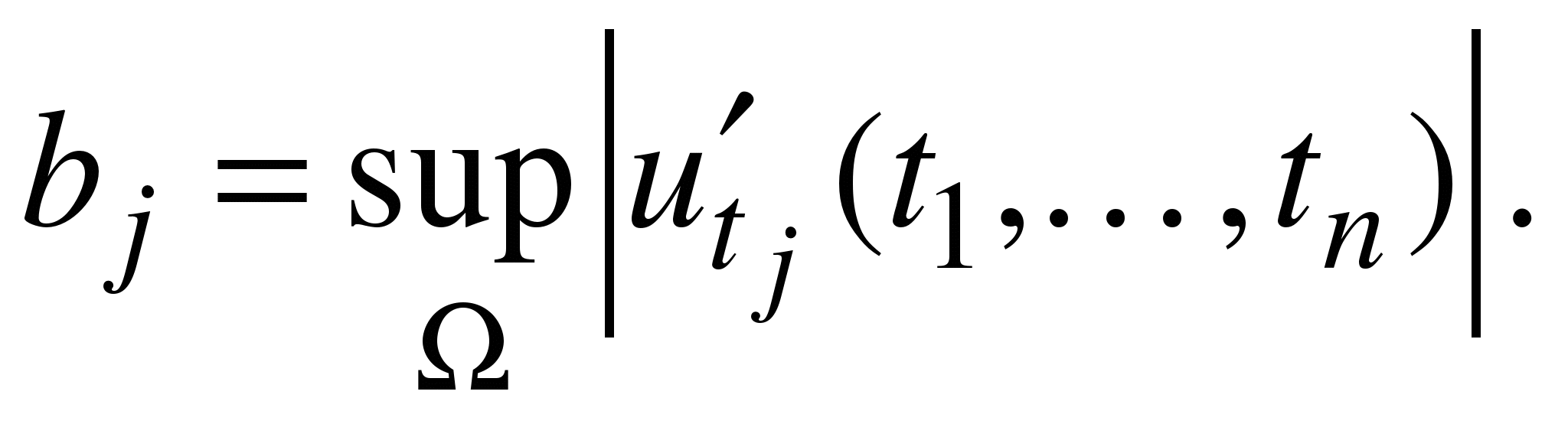 Можно
показать, что при малых Можно
показать, что при малых  это
оценка не может быть существенно
улучшена. На практике иногда
пользуются грубой (линейной)
оценкой это
оценка не может быть существенно
улучшена. На практике иногда
пользуются грубой (линейной)
оценкой где где Несложно
показать, чтоа) Несложно
показать, чтоа)
 предельная
погрешность суммы или разности
равна сумме или разности
предельных погрешностей.в)
Предельная относительная
погрешность произведения
или частного приближенного
равна сумме предельных
относительных
погрешностей предельная
погрешность суммы или разности
равна сумме или разности
предельных погрешностей.в)
Предельная относительная
погрешность произведения
или частного приближенного
равна сумме предельных
относительных
погрешностей
 Погрешность
метода
Оценим
погрешность при вычислении
первой производной при помощи
соотношения Погрешность
метода
Оценим
погрешность при вычислении
первой производной при помощи
соотношения
 : : гдеO(h)
есть погрешность метода. В
данном случае под погрешностью
метода понимается абсолютная
величина разности гдеO(h)
есть погрешность метода. В
данном случае под погрешностью
метода понимается абсолютная
величина разности
 ,
которая составляетO(h)
(более точно ,
которая составляетO(h)
(более точно
 ,
где ,
где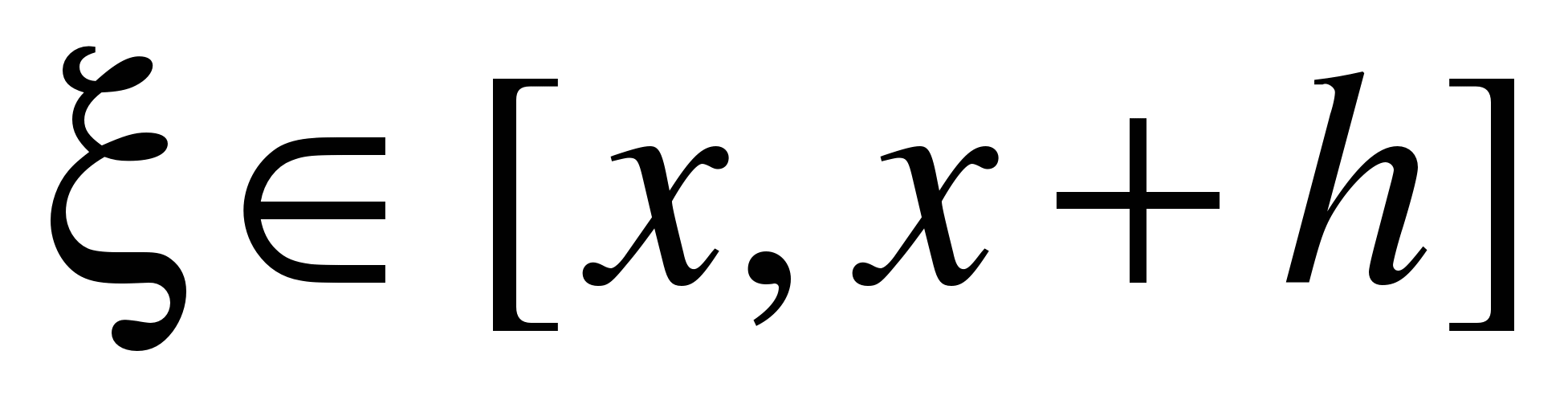 ).
Если
же взять другой метод вычисления
производной ).
Если
же взять другой метод вычисления
производной ,
то получим, что его погрешность
составляетO(h2),
это оказывается существенным
при малых h.
Однако уменьшать h
до бесконечности не имеет
смысла, что видно из следующего
примера. Реальная погрешность
при вычислении первой
производной будет ,
то получим, что его погрешность
составляетO(h2),
это оказывается существенным
при малых h.
Однако уменьшать h
до бесконечности не имеет
смысла, что видно из следующего
примера. Реальная погрешность
при вычислении первой
производной будет
 поскольку
погрешность за счет машинного
округления составит поскольку
погрешность за счет машинного
округления составит .
В
этом случае можно найти
оптимальный шагh.
Будем
считать полную погрешность
в вычислении производной Δ
функцией шага h.
Отыщем минимум этой функции.
Приравняв производную .
В
этом случае можно найти
оптимальный шагh.
Будем
считать полную погрешность
в вычислении производной Δ
функцией шага h.
Отыщем минимум этой функции.
Приравняв производную
 к
нулю, получим оптимальный
шаг численного
дифференцирования к
нулю, получим оптимальный
шаг численного
дифференцирования Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти
из-за возрастания вклада
ошибок округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения
производной подробнее.
Пусть
задана таблица значений xi.
В дальнейшем совокупность
точек на отрезке, котором
проводятся вычисления, иногда
будут называться сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная,
и расстояние между узлами
равно Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти
из-за возрастания вклада
ошибок округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения
производной подробнее.
Пусть
задана таблица значений xi.
В дальнейшем совокупность
точек на отрезке, котором
проводятся вычисления, иногда
будут называться сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная,
и расстояние между узлами
равно
 —шагу
сетки.
Пусть узлы сетки пронумерованы
в порядке возрастания,
т.е. —шагу
сетки.
Пусть узлы сетки пронумерованы
в порядке возрастания,
т.е.
  , ,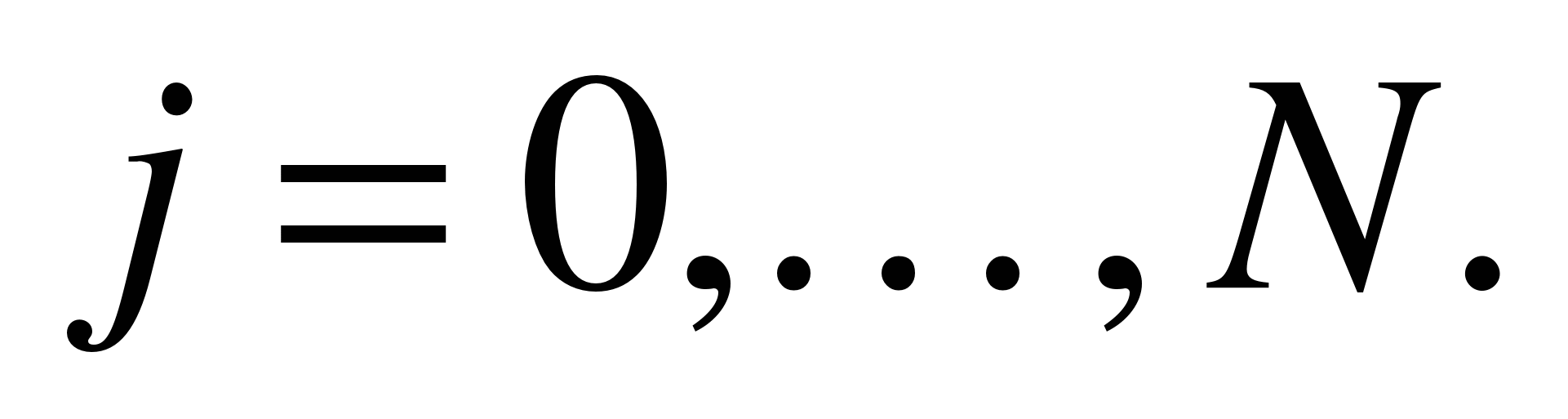 Пусть Пусть —
функция, определенная в узлах
сетки. Такие функции будут
называться табличными, или
сеточными функциями. Считаем,
кроме того, что рассматриваемая
сеточная функция есть проекция
(или ограничение) на сетку
некоторой гладкой нужное
число раз непрерывно
дифференцируемой функцииf(x).
По определению производной —
функция, определенная в узлах
сетки. Такие функции будут
называться табличными, или
сеточными функциями. Считаем,
кроме того, что рассматриваемая
сеточная функция есть проекция
(или ограничение) на сетку
некоторой гладкой нужное
число раз непрерывно
дифференцируемой функцииf(x).
По определению производной
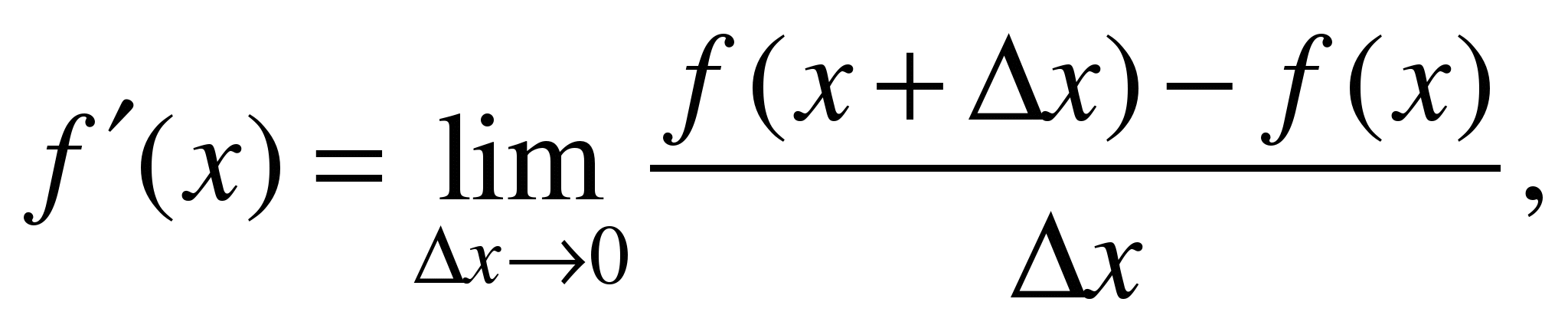 тогда,
если шаг сетки достаточно
мал, по аналогии можно написать
формулу в конечных разностях,
дающую приближенное значение
производной сеточной
функции: тогда,
если шаг сетки достаточно
мал, по аналогии можно написать
формулу в конечных разностях,
дающую приближенное значение
производной сеточной
функции: (1.1)
Если
параметр (1.1)
Если
параметр достаточно
мал, то можно считать полученное
значение производной достаточно
точным. Погрешность формулы
(1.1) оценена в пункте 1.4. Как
показано выше, при уменьшении
шага сеткиh
ошибка будет уменьшаться, но
при некотором значении достаточно
мал, то можно считать полученное
значение производной достаточно
точным. Погрешность формулы
(1.1) оценена в пункте 1.4. Как
показано выше, при уменьшении
шага сеткиh
ошибка будет уменьшаться, но
при некотором значении
 ошибка
может возрасти до бесконечности.
При оценке погрешности метода
обычно считается, что все
вычисления были точными. Но
существует ошибка округления.
При оценке ее большую роль
играет машинный ε — мера
относительной погрешности
машинного округления,
возникающей из-за конечной
разрядности мантиссы при
работе с числами в формате с
плавающей точкой. Напомним,
что по определению машинным
ε называют наибольшее из
чисел, для которых в рамках
используемой системы
вычислений, выполнено
1 + ε = 1. Тогда
абсолютная погрешность при
вычислении значения функции
(или представлении табличной
функции) есть ошибка
может возрасти до бесконечности.
При оценке погрешности метода
обычно считается, что все
вычисления были точными. Но
существует ошибка округления.
При оценке ее большую роль
играет машинный ε — мера
относительной погрешности
машинного округления,
возникающей из-за конечной
разрядности мантиссы при
работе с числами в формате с
плавающей точкой. Напомним,
что по определению машинным
ε называют наибольшее из
чисел, для которых в рамках
используемой системы
вычислений, выполнено
1 + ε = 1. Тогда
абсолютная погрешность при
вычислении значения функции
(или представлении табличной
функции) есть Максимальный
вклад погрешностей округления
при вычислении производной
по формуле (1.1) будет Максимальный
вклад погрешностей округления
при вычислении производной
по формуле (1.1) будет тогда,
когда члены в знаменателе
(1.1) имеют ошибки разных
знаков.
Пусть тогда,
когда члены в знаменателе
(1.1) имеют ошибки разных
знаков.
Пусть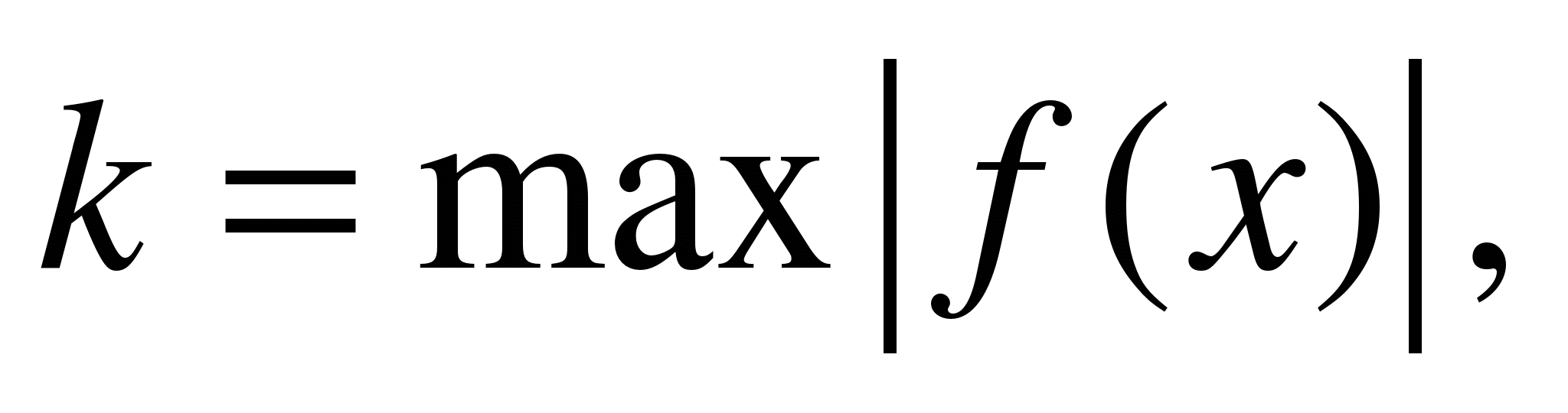 максимум
ищется на отрезке, на котором
вычисляются значения
производных. Тогда суммарная
ошибка, состоящая из погрешности
метода и погрешности округления,
есть максимум
ищется на отрезке, на котором
вычисляются значения
производных. Тогда суммарная
ошибка, состоящая из погрешности
метода и погрешности округления,
есть  Для
вычисления оптимального шага
численного дифференцирования
найдем минимум суммарной
ошибки, как функции шага сетки Для
вычисления оптимального шага
численного дифференцирования
найдем минимум суммарной
ошибки, как функции шага сетки откуда откуда Если
требуется повысить точность
вычисления производных,
необходимо воспользоваться
формулами, имеющими меньшие
погрешности метода. Так, из
курсов математического
анализа известно, что Если
требуется повысить точность
вычисления производных,
необходимо воспользоваться
формулами, имеющими меньшие
погрешности метода. Так, из
курсов математического
анализа известно, что По
аналогии напишем конечно-разностную
формулу По
аналогии напишем конечно-разностную
формулу (1.2)
(1.2)
— формула с центральной
разностью. Исследуем ее на
аппроксимацию, т.е. оценим
погрешность метода. Предположим,
что функция, которую
спроектировали на сетку,
трижды непрерывно дифференцируема,
тогда (1.2)
(1.2)
— формула с центральной
разностью. Исследуем ее на
аппроксимацию, т.е. оценим
погрешность метода. Предположим,
что функция, которую
спроектировали на сетку,
трижды непрерывно дифференцируема,
тогда  Погрешность
метода определяется 3-й
производной функции. Введем Погрешность
метода определяется 3-й
производной функции. Введем тогда
суммарная погрешность при
вычислении по формуле с
центральной разностью
есть тогда
суммарная погрешность при
вычислении по формуле с
центральной разностью
есть для
вычисления оптимального
шага, находя минимум погрешности,
как функции шага сетки, имеем для
вычисления оптимального
шага, находя минимум погрешности,
как функции шага сетки, имеем откуда откуда Для
более точного вычисления
производной, необходимо
использовать, разложение
более высокого порядка, шаг Для
более точного вычисления
производной, необходимо
использовать, разложение
более высокого порядка, шаг будет
увеличиваться.
Формула
(1.1) — двухточечная, (1.2) —
трехточечная: при вычислении
производной используются
точки (узлы) будет
увеличиваться.
Формула
(1.1) — двухточечная, (1.2) —
трехточечная: при вычислении
производной используются
точки (узлы) (узел
входит с нулевым коэффициентом), (узел
входит с нулевым коэффициентом), , , —
совокупность узлов, участвующих
в каждом вычислении производной,
в дальнейшем будем иногда
называтьсеточным
шаблоном.
Введем
на рассматриваемом отрезке
шаблон из нескольких
точек.
Считаем, что сетка
равномерная — шаг сетки
постоянный, расстояния между
любыми двумя соседними узлами
равны. Используем для вычисления
значения первой производной
следующую приближенную
(конечноразностную)
формулу: —
совокупность узлов, участвующих
в каждом вычислении производной,
в дальнейшем будем иногда
называтьсеточным
шаблоном.
Введем
на рассматриваемом отрезке
шаблон из нескольких
точек.
Считаем, что сетка
равномерная — шаг сетки
постоянный, расстояния между
любыми двумя соседними узлами
равны. Используем для вычисления
значения первой производной
следующую приближенную
(конечноразностную)
формулу:
 (1.3)
шаблон
включаетl
точек слева от рассматриваемой
точки xj
и m
справа. Коэффициенты α —
неопределенные
коэффициенты.
Формула дифференцирования
может быть и односторонней
— либо l,
либо
m могут
равняться нулю. В первом
случае иногда называют (на
наш взгляд, не слишком удачно)
такую приближенную формулу
формулой дифференцирования
вперед, во втором — формулой
дифференцирования назад.
Потребуем, чтобы (1.3) приближала
первую производную с точностью (1.3)
шаблон
включаетl
точек слева от рассматриваемой
точки xj
и m
справа. Коэффициенты α —
неопределенные
коэффициенты.
Формула дифференцирования
может быть и односторонней
— либо l,
либо
m могут
равняться нулю. В первом
случае иногда называют (на
наш взгляд, не слишком удачно)
такую приближенную формулу
формулой дифференцирования
вперед, во втором — формулой
дифференцирования назад.
Потребуем, чтобы (1.3) приближала
первую производную с точностью
 Используем
разложения в ряд Тейлора в
окрестности точкиxj.
Подставляя их в (1.3),
получим Используем
разложения в ряд Тейлора в
окрестности точкиxj.
Подставляя их в (1.3),
получим
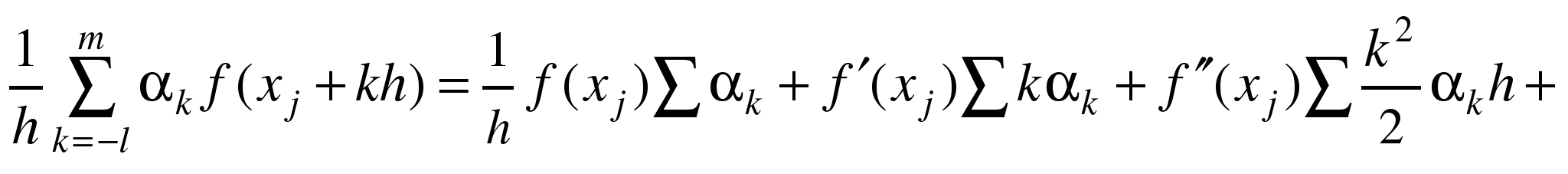  Потребуем
выполнение условий: Потребуем
выполнение условий:   …, …, …
(1.4)
Получаем систему
линейных алгебраических
уравнений для неопределенных
коэффициентов α (1.4). Матрица
этой системы есть …
(1.4)
Получаем систему
линейных алгебраических
уравнений для неопределенных
коэффициентов α (1.4). Матрица
этой системы есть Вектор
правых частей
(0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не
равен нулю. Тогда существует
единственный набор коэффициентов
α, который позволяет найти
на шаблоне из (1 + l + m)
точек значение первой
производной с точностью Вектор
правых частей
(0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не
равен нулю. Тогда существует
единственный набор коэффициентов
α, который позволяет найти
на шаблоне из (1 + l + m)
точек значение первой
производной с точностью
 Для
нахождения второй производной
можно использовать ту же
самую формулу (1.3) с небольшой
модификацией Для
нахождения второй производной
можно использовать ту же
самую формулу (1.3) с небольшой
модификацией только
теперь только
теперь  Очевидно,
что и данная система уравнений
для нахождения неопределенных
коэффициентов имеет единственное
решение. Для получения с той
же точностью приближенных
значений производных до
порядкаl + m
включительно
с точностью Очевидно,
что и данная система уравнений
для нахождения неопределенных
коэффициентов имеет единственное
решение. Для получения с той
же точностью приближенных
значений производных до
порядкаl + m
включительно
с точностью
 модификации
формулы (1.3) и условий (1.4)
очевидны, набор неопределенных
коэффициентов находится
единственным образом.
Таким
образом, доказано следующее
утверждение. На сеточном
шаблоне, включающем в себяN + 1
точку, с помощью метода
неопределенных коэффициентов
всегда можно построить
единственную формулу для
вычисления производной от
первого до N
порядка включительно с
точностью модификации
формулы (1.3) и условий (1.4)
очевидны, набор неопределенных
коэффициентов находится
единственным образом.
Таким
образом, доказано следующее
утверждение. На сеточном
шаблоне, включающем в себяN + 1
точку, с помощью метода
неопределенных коэффициентов
всегда можно построить
единственную формулу для
вычисления производной от
первого до N
порядка включительно с
точностью
 .
Утверждение
доказано для равномерной
сетки, но на случай произвольных
расстояний между сеточными
узлами обобщение проводится
легко.
Так как на практике
вычисления проводятся с
конечной длиной мантиссы, то
получить нулевую ошибку
невозможно. .
Утверждение
доказано для равномерной
сетки, но на случай произвольных
расстояний между сеточными
узлами обобщение проводится
легко.
Так как на практике
вычисления проводятся с
конечной длиной мантиссы, то
получить нулевую ошибку
невозможно. |

|
|

|
|
|
|
|
|
|
|
|
|
|
|
.

|
|
Начало
формы
|


 Определение.
Относительной
погрешностью
называется величина
Определение.
Относительной
погрешностью
называется величина
 где
где где
где Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти из-за
возрастания вклада ошибок
округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения производной
подробнее.
Пусть задана таблица
значений xi.
В дальнейшем совокупность точек
на отрезке, котором проводятся
вычисления, иногда будут называться
сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная, и
расстояние между узлами равно
Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти из-за
возрастания вклада ошибок
округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения производной
подробнее.
Пусть задана таблица
значений xi.
В дальнейшем совокупность точек
на отрезке, котором проводятся
вычисления, иногда будут называться
сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная, и
расстояние между узлами равно
 Если
требуется повысить точность
вычисления производных, необходимо
воспользоваться формулами, имеющими
меньшие погрешности метода. Так,
из курсов математического анализа
известно, что
Если
требуется повысить точность
вычисления производных, необходимо
воспользоваться формулами, имеющими
меньшие погрешности метода. Так,
из курсов математического анализа
известно, что Для
более точного вычисления производной,
необходимо использовать, разложение
более высокого порядка, шаг
Для
более точного вычисления производной,
необходимо использовать, разложение
более высокого порядка, шаг
 Вектор
правых частей (0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не равен
нулю. Тогда существует единственный
набор коэффициентов α, который
позволяет найти на шаблоне из
(1 + l + m)
точек значение первой производной
с точностью
Вектор
правых частей (0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не равен
нулю. Тогда существует единственный
набор коэффициентов α, который
позволяет найти на шаблоне из
(1 + l + m)
точек значение первой производной
с точностью
 Определение.
Относительной
погрешностью
называется величина
Определение.
Относительной
погрешностью
называется величина
 где
где где
где Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти
из-за возрастания вклада
ошибок округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения
производной подробнее.
Пусть
задана таблица значений xi.
В дальнейшем совокупность
точек на отрезке, котором
проводятся вычисления, иногда
будут называться сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная,
и расстояние между узлами
равно
Выбирать
значениеh
меньше оптимального не имеет
смысла, так как при дальнейшем
уменьшении шага суммарная
погрешность начинает расти
из-за возрастания вклада
ошибок округления.
Задача
численного дифференцирования
Рассмотрим
задачу приближенного вычисления
приближенного значения
производной подробнее.
Пусть
задана таблица значений xi.
В дальнейшем совокупность
точек на отрезке, котором
проводятся вычисления, иногда
будут называться сеткой,
каждое значение xi
— узлом
сетки. Пусть сетка равномерная,
и расстояние между узлами
равно
 Если
требуется повысить точность
вычисления производных,
необходимо воспользоваться
формулами, имеющими меньшие
погрешности метода. Так, из
курсов математического
анализа известно, что
Если
требуется повысить точность
вычисления производных,
необходимо воспользоваться
формулами, имеющими меньшие
погрешности метода. Так, из
курсов математического
анализа известно, что Для
более точного вычисления
производной, необходимо
использовать, разложение
более высокого порядка, шаг
Для
более точного вычисления
производной, необходимо
использовать, разложение
более высокого порядка, шаг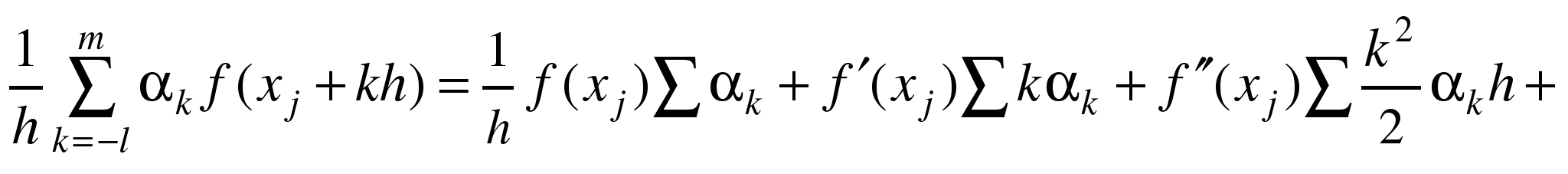
 Вектор
правых частей
(0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не
равен нулю. Тогда существует
единственный набор коэффициентов
α, который позволяет найти
на шаблоне из (1 + l + m)
точек значение первой
производной с точностью
Вектор
правых частей
(0, 1, 0, …,0)T.
Определитель
данной матрицы — детерминант
Вандермонда. Из курса линейной
алгебры следует, что он не
равен нулю. Тогда существует
единственный набор коэффициентов
α, который позволяет найти
на шаблоне из (1 + l + m)
точек значение первой
производной с точностью