4.12.3. Краевые условия 2-го и 3-го рода.

Рассмотрим теперь уравнение (28) с краевыми условиями 2-го или 3-го рода (30):

Будем решать эту задачу с помощью трехточечной разностной схемы (31) с условиями на коэффициенты (34). При этих условиях, как было показано, схема имеет второй порядок аппроксимации. В таком случае возникает вопрос: как аппроксимировать краевые условия ? Если пользоваться для этого односторонними разностными производными, как в методе Эйлера, то краевые условия запишутся в виде

,

однако, как хорошо известно (см. п. 4.3.2), такие формулы будут иметь погрешность аппроксимации первого порядка. Чтобы краевые условия не снижали порядок аппроксции разностной схемы (31), необходимо воспользоваться односторонними разностными аппроксимациями производных, имеющими второй порядок по . Например, для этих целей подходит разностная производная

,

где, как обычно, . Действительно, по формулам Тейлора

, ,

поэтому

.

При использовании подобных формул разностные аппроксимации краевых условий принимают вид

В такой ситуации для разрешения трехточечной схемы (31) также может быть использован метод прогонки, рассмотренный в п. 4.12.2. Действительно, уравнение

на левом краю интервала составляет с краевым условием систему

,

из которой можно исключить , при этом система преобразуется в уравнение

с некоторыми вполне определенными коэффициентами . Действуя аналогично п. 4.12.2, можно записать разностную схему в виде уравнений

, (40)

где коэффициенты считаются по рекуррентным формулам (39), исходя из значений. На правом конце отрезка получаем систему

,

из которой можно найти , а следом - и все остальные(по рекуррентным формулам (40)).

[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]

[Home|Кафедра|ПетрГУ]

[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]

[Home|Кафедра|ПетрГУ]

 

     

[Home|Кафедра|ПетрГУ]

   

1.1. Методы решения алгебраических уравнений

1.1.1. Приближенное решение уравнений методом хорд.

Тема: Графическое отделение и вычисление методом хорд наименьшего положительного корня уравнения f(x)=0 с точностью.

Пример.

Для графического отделения корня необходимо построить график функции f(x), составив таблицу значений функции на интервале [0,2] с шагом равным 0.2

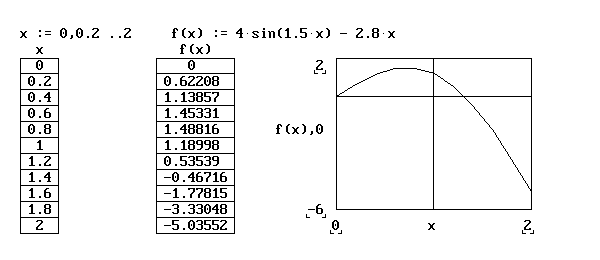
С помощью рисунка можно определить, что положительный корень лежит в промежутке [1.2, 1.4].

Для уточнения корня методом хорд проверяется достаточное условие применимости метода. Для этого определяются знаки функции и второй производной на концах выбранного промежутка. За начальное приближение принимается то из чисел, для которого эти знаки одинаковы.

Вычисления по формулам производятся до тех пор, пока не совпадут две последние итерации. Значение функции при x=1,31492 равно нулю, следовательно корень уравнения равен 1,31492.

Значение корня можно получить, используя стандартную функцию пакета root, предназначенную для нахождения корня уравнения, задавz=1,4 (приблизительное значение корня).

Корень уравнения равен 1.31492.

 

1.1.2. Приближенное решение уравнений методом касательных.

Тема: Графическое отделение и вычисление методом касательных наименьшего положительного корня уравнения f(x)=0 с точностью.

Пример.

Для графического отделения корня необходимо построить график функции f(x), составив таблицу значений функции на интервале [0,2] с шагом равным 0.2

С помощью рисунка можно определить, что положительный корень лежит в промежутке [1.2, 1.4].

Для уточнения корня методом касательных проверяется достаточное условие применимости метода. Для этого определяются знаки функции и второй производной на концах выбранного промежутка. За начальное приближение принимается то из чисел, для которого эти знаки одинаковы.

Вычисления по формулам производятся до тех пор, пока не совпадут две последние итерации. Значение функции при x=1,31492 равно нулю, следовательно корень уравнения равен 1,31492.

Значение корня можно получить, используя стандартную функцию пакета root, предназначенную для нахождения корня уравнения, задавz=1,4 (приблизительное значение корня).

Корень уравнения равен 1.31492.

 

 

1.1.3. Приближенное решение уравнений комбинированным методом хорд касательных.

Тема: Графическое отделение и вычисление комбинированным методом хорд и касательных наименьшего положительного корня уравнения f(x)=0 с точностью.

Пример.

Для графического отделения корня необходимо построить график функции f(x), составив таблицу значений функции на интервале [0,2] с шагом равным 0.2

С помощью рисунка можно определить, что положительный корень лежит в промежутке [1.2, 1.4].

Для уточнения корня комбинированным методом хорд и касательных проверяется достаточное условие применимости метода. Для этого определяются знаки функции и второй производной на концах выбранного промежутка.

За начальное приближение принимается то из чисел, для которого эти знаки одинаковы. За следующее приближение принимается другой конец промежутка. Вычисления по формулам производятся до тех пор, пока не совпадут две последние итерации. Значение функции при x=1,31492 равно нулю, следовательно корень уравнения равен 1,31492.

Значение корня можно получить, используя стандартную функцию пакета root, предназначенную для нахождения корня уравнения, задавz=1,4 (приблизительное значение корня).

Корень уравнения равен 1.31492.