3.5.1. Линейный интерполяционный сплайн

Пусть - разбиение отрезка.

, - заданные значения.

Сплайном первой степени называется :непрерывная на отрезке , линейная на каждом частичном промежуткефункция. Его обозначение. Интерполяционным для данной функцииназывается сплайн, удовлетворяющий условиям,.

График линейного интерполяционного сплайна - это ломаная, проходящая через заданные точки.

Пусть ,. Выражение для сплайнана этом промежутке:

Остаточный член : .

Оценка остаточного члена зависит от дифференцируемых свойств функции .

Пусть . Обозначение

- колебание функции на

Справедлива следующая лемма:

Лемма (вариант теоремы о среднем):

Пусть . Если величиныодинакового знака, то существуеттакое, что

С помощью этой леммы доказывается следующая теорема об оценке остаточного члена линейного интерполяционного сплайна.

Теорема

Если , то. Действительно,

, где . По приведенной выше лемме

, где

С улучшением гладкости функции оценка погрешности ее интерполяции линейными сплайнами также улучшается. А именно,

если , то, где

Для можно получить оценку.

Дальнейшее увеличение гладкости функции не дает повышения порядка аппроксимации. Происходит насыщение алгоритма.

Сходимость.

Пусть на задана последовательность сеток:,, которая удовлетворяют условиюпри. Длястроится интерполяционный сплайн. Интерполяционный процесс сходится, еслипридля любой функциииз некоторого класса . Отсюда вытекает возможность интерполяции с наперед заданной точностью:

.

Преимущество по сравнению с интерполяционными многочленами: из оценки погрешности следует сходимость.

Пусть . По доказанной теореме.

По определению при, поэтому процесс интерполяции линейными сплайнами сходится на множестве непрерывных функций по произвольной последовательности сеток.

Если ,, то. Сходимость порядка.

3.5.2. Кубический интерполяционный сплайн

Пусть на задана сетка, в узлах которой известны значения функции. Сплайн третьей степени, интерполирующий заданную функцию, определяется как функция, удовлетворяющая условиям:

1)

2) Для любого частичного промежутка -многочлен третьей степени

3)

Для задания надо определить 4 коэффициента для каждого промежутка, т.е.параметров.

Условия 1) требуют чтобы во внутренних узлах сплайн и его производные до 2-го порядка были непрерывны.

Это дает условия для определения параметров, ещеусловие содержится в 3).

Итого имеем условия. Еще 2 условия, необходимые для однозначного определения сплайна, обычно задаются в виде граничных условий, т.е. условий в точкахи.

Возьмем в качестве граничных условия

4)

Для построения кубического интерполяционного сплайна могут быть использованы различные подходы. Проведем построение сплайна, исходя из условий 1) - 4). Из 1) и 2) следует, что ??? непрерывная функция, линейная на каждом т.е. ??? - линейный сплайн.

Обозначив , получаем

(33)

для .

Интегрируя (5), получаем

(34)

(35)

и - постоянные интегрирования.

Условия 3) дают:

(36)

Из (36) получаем:

Подставляя ив (7), получаем:

(37)

После преобразования

из (37) получаем

(38)

Из (34) получаем

(39)

Из (39) находим односторонние пределы производной для узла ,

(40)

(41)

Подставляя (40) и (41) в условие непрерывности в узлеполучаем :

(42)

Дополняя (42) равенствами из условия 4) : , получаем систему уравнений относительновида :

(43) с квадратной матрицей .

и квадратной матрицей

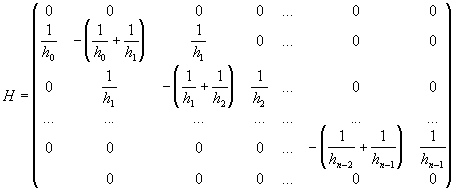
Координатами вектора являются значения.

Для матрицы ненулевые элементы расположены на главной диагонали и двух соседних с ней. Такие матрицы называются трехдиагональными. Длявыполнено условие диагонального преобладания.

Матрица с диагональным преобладанием невырождена. Следовательно, система (42) однозначно разрешима, т.е. существует единственный кубический интерполяционный сплайн. Кроме условий 4) - условий "свободного провисания" интерполяционной кривой в точках и, могут быть известны наклоны интерполяционной кривой в граничных точках. Тогда условия на границах имеют вид:

(44) Могут быть использованы и другие варианты.

Вид граничных условий меняет некоторые элементы матрицы , но в любом случае она остается матрицей с диагональным преобладанием.

Решение системы (43) с трехдиагональной матрицей может быть найдено посредством специального варианта метода последовательного исключения неизвестных, который называется методом прогонки.

Относительно оценки погрешности и сходимости интерполяций кубическими сплайнами имеют место следующие результаты:

если , то, где,,

если ,, то оценка имеет вид для. Из этих оценок следует сходимость интерполяционного процесса на последовательности сеток.