
- •Contents
- •Preface
- •1 Spread spectrum signals and systems
- •1.1 Basic definition
- •1.2 Historical sketch
- •2 Classical reception problems and signal design
- •2.1 Gaussian channel, general reception problem and optimal decision rules
- •2.2 Binary data transmission (deterministic signals)
- •2.3 M-ary data transmission: deterministic signals
- •2.4 Complex envelope of a bandpass signal
- •2.5 M-ary data transmission: noncoherent signals
- •2.6 Trade-off between orthogonal-coding gain and bandwidth
- •2.7 Examples of orthogonal signal sets
- •2.7.1 Time-shift coding
- •2.7.2 Frequency-shift coding
- •2.7.3 Spread spectrum orthogonal coding
- •2.8 Signal parameter estimation
- •2.8.1 Problem statement and estimation rule
- •2.8.2 Estimation accuracy
- •2.9 Amplitude estimation
- •2.10 Phase estimation
- •2.11 Autocorrelation function and matched filter response
- •2.12 Estimation of the bandpass signal time delay
- •2.12.1 Estimation algorithm
- •2.12.2 Estimation accuracy
- •2.13 Estimation of carrier frequency
- •2.14 Simultaneous estimation of time delay and frequency
- •2.15 Signal resolution
- •2.16 Summary
- •Problems
- •Matlab-based problems
- •3 Merits of spread spectrum
- •3.1 Jamming immunity
- •3.1.1 Narrowband jammer
- •3.1.2 Barrage jammer
- •3.2 Low probability of detection
- •3.3 Signal structure secrecy
- •3.4 Electromagnetic compatibility
- •3.5 Propagation effects in wireless systems
- •3.5.1 Free-space propagation
- •3.5.2 Shadowing
- •3.5.3 Multipath fading
- •3.5.4 Performance analysis
- •3.6 Diversity
- •3.6.1 Combining modes
- •3.6.2 Arranging diversity branches
- •3.7 Multipath diversity and RAKE receiver
- •Problems
- •Matlab-based problems
- •4 Multiuser environment: code division multiple access
- •4.1 Multiuser systems and the multiple access problem
- •4.2 Frequency division multiple access
- •4.3 Time division multiple access
- •4.4 Synchronous code division multiple access
- •4.5 Asynchronous CDMA
- •4.6 Asynchronous CDMA in the cellular networks
- •4.6.1 The resource reuse problem and cellular systems
- •4.6.2 Number of users per cell in asynchronous CDMA
- •Problems
- •Matlab-based problems
- •5 Discrete spread spectrum signals
- •5.1 Spread spectrum modulation
- •5.2 General model and categorization of discrete signals
- •5.3 Correlation functions of APSK signals
- •5.4 Calculating correlation functions of code sequences
- •5.5 Correlation functions of FSK signals
- •5.6 Processing gain of discrete signals
- •Problems
- •Matlab-based problems
- •6 Spread spectrum signals for time measurement, synchronization and time-resolution
- •6.1 Demands on ACF: revisited
- •6.2 Signals with continuous frequency modulation
- •6.3 Criterion of good aperiodic ACF of APSK signals
- •6.4 Optimization of aperiodic PSK signals
- •6.5 Perfect periodic ACF: minimax binary sequences
- •6.6 Initial knowledge on finite fields and linear sequences
- •6.6.1 Definition of a finite field
- •6.6.2 Linear sequences over finite fields
- •6.6.3 m-sequences
- •6.7 Periodic ACF of m-sequences
- •6.8 More about finite fields
- •6.9 Legendre sequences
- •6.10 Binary codes with good aperiodic ACF: revisited
- •6.11 Sequences with perfect periodic ACF
- •6.11.1 Binary non-antipodal sequences
- •6.11.2 Polyphase codes
- •6.11.3 Ternary sequences
- •6.12 Suppression of sidelobes along the delay axis
- •6.12.1 Sidelobe suppression filter
- •6.12.2 SNR loss calculation
- •6.13 FSK signals with optimal aperiodic ACF
- •Problems
- •Matlab-based problems
- •7 Spread spectrum signature ensembles for CDMA applications
- •7.1 Data transmission via spread spectrum
- •7.1.1 Direct sequence spreading: BPSK data modulation and binary signatures
- •7.1.2 DS spreading: general case
- •7.1.3 Frequency hopping spreading
- •7.2 Designing signature ensembles for synchronous DS CDMA
- •7.2.1 Problem formulation
- •7.2.2 Optimizing signature sets in minimum distance
- •7.2.3 Welch-bound sequences
- •7.3 Approaches to designing signature ensembles for asynchronous DS CDMA
- •7.4 Time-offset signatures for asynchronous CDMA
- •7.5 Examples of minimax signature ensembles
- •7.5.1 Frequency-offset binary m-sequences
- •7.5.2 Gold sets
- •7.5.3 Kasami sets and their extensions
- •7.5.4 Kamaletdinov ensembles
- •Problems
- •Matlab-based problems
- •8 DS spread spectrum signal acquisition and tracking
- •8.1 Acquisition and tracking procedures
- •8.2 Serial search
- •8.2.1 Algorithm model
- •8.2.2 Probability of correct acquisition and average number of steps
- •8.2.3 Minimizing average acquisition time
- •8.3 Acquisition acceleration techniques
- •8.3.1 Problem statement
- •8.3.2 Sequential cell examining
- •8.3.3 Serial-parallel search
- •8.3.4 Rapid acquisition sequences
- •8.4 Code tracking
- •8.4.1 Delay estimation by tracking
- •8.4.2 Early–late DLL discriminators
- •8.4.3 DLL noise performance
- •Problems
- •Matlab-based problems
- •9 Channel coding in spread spectrum systems
- •9.1 Preliminary notes and terminology
- •9.2 Error-detecting block codes
- •9.2.1 Binary block codes and detection capability
- •9.2.2 Linear codes and their polynomial representation
- •9.2.3 Syndrome calculation and error detection
- •9.2.4 Choice of generator polynomials for CRC
- •9.3 Convolutional codes
- •9.3.1 Convolutional encoder
- •9.3.2 Trellis diagram, free distance and asymptotic coding gain
- •9.3.3 The Viterbi decoding algorithm
- •9.3.4 Applications
- •9.4 Turbo codes
- •9.4.1 Turbo encoders
- •9.4.2 Iterative decoding
- •9.4.3 Performance
- •9.4.4 Applications
- •9.5 Channel interleaving
- •Problems
- •Matlab-based problems
- •10 Some advancements in spread spectrum systems development
- •10.1 Multiuser reception and suppressing MAI
- •10.1.1 Optimal (ML) multiuser rule for synchronous CDMA
- •10.1.2 Decorrelating algorithm
- •10.1.3 Minimum mean-square error detection
- •10.1.4 Blind MMSE detector
- •10.1.5 Interference cancellation
- •10.1.6 Asynchronous multiuser detectors
- •10.2 Multicarrier modulation and OFDM
- •10.2.1 Multicarrier DS CDMA
- •10.2.2 Conventional MC transmission and OFDM
- •10.2.3 Multicarrier CDMA
- •10.2.4 Applications
- •10.3 Transmit diversity and space–time coding in CDMA systems
- •10.3.1 Transmit diversity and the space–time coding problem
- •10.3.2 Efficiency of transmit diversity
- •10.3.3 Time-switched space–time code
- •10.3.4 Alamouti space–time code
- •10.3.5 Transmit diversity in spread spectrum applications
- •Problems
- •Matlab-based problems
- •11 Examples of operational wireless spread spectrum systems
- •11.1 Preliminary remarks
- •11.2 Global positioning system
- •11.2.1 General system principles and architecture
- •11.2.2 GPS ranging signals
- •11.2.3 Signal processing
- •11.2.4 Accuracy
- •11.2.5 GLONASS and GNSS
- •11.2.6 Applications
- •11.3 Air interfaces cdmaOne (IS-95) and cdma2000
- •11.3.1 Introductory remarks
- •11.3.2 Spreading codes of IS-95
- •11.3.3 Forward link channels of IS-95
- •11.3.3.1 Pilot channel
- •11.3.3.2 Synchronization channel
- •11.3.3.3 Paging channels
- •11.3.3.4 Traffic channels
- •11.3.3.5 Forward link modulation
- •11.3.3.6 MS processing of forward link signal
- •11.3.4 Reverse link of IS-95
- •11.3.4.1 Reverse link traffic channel
- •11.3.4.2 Access channel
- •11.3.4.3 Reverse link modulation
- •11.3.5 Evolution of air interface cdmaOne to cdma2000
- •11.4 Air interface UMTS
- •11.4.1 Preliminaries
- •11.4.2 Types of UMTS channels
- •11.4.3 Dedicated physical uplink channels
- •11.4.4 Common physical uplink channels
- •11.4.5 Uplink channelization codes
- •11.4.6 Uplink scrambling
- •11.4.7 Mapping downlink transport channels to physical channels
- •11.4.8 Downlink physical channels format
- •11.4.9 Downlink channelization codes
- •11.4.10 Downlink scrambling codes
- •11.4.11 Synchronization channel
- •11.4.11.1 General structure
- •11.4.11.2 Primary synchronization code
- •11.4.11.3 Secondary synchronization code
- •References
- •Index

316 Spread Spectrum and CDMA
10.1.6 Asynchronous multiuser detectors
Although the multiuser detection algorithms briefly discussed above are tailored to synchronous CDMA, they are, after an appropriate modification, extendable to the asynchronous case, too. Let us come back to (10.6) and adapt it to the asynchronous situation illustrated by Figure 7.15, assuming alignment of chip boundaries of all users and operating with only baseband real signatures (i.e. ignoring mutual phase shifts of bandpass signatures). Assume also that all signatures are periodic with period equal to
bit duration T ¼ Tb and |
consider as before the first user receiver ( 1 ¼ 0) at the |
||||
observation interval of data bit number zero. Then: |
|
||||
y t |
8 A1b1;0s1 |
ðtÞ þ kK2 |
Akbk; 1skðt kÞ þ nðtÞ; 0 < t 1 |
10:25 |
|
> |
|
X |
|
||
ð Þ ¼ |
> |
|
K |
ð Þ |
|
> |
|
|
|||
|
> |
|
|
|
|
|
< |
|
¼ |
|
|
|
> |
|
X |
|
|
|
> |
|
ðtÞ þ |
Akbk;0skðt kÞ þ nðtÞ; 1 < t T |
|
|
> |
A1b1;0s1 |
|
||
|
> |
|
|
|
|
|
: |
|
|
|
|
k¼2
As (10.25) shows, the character of MAI created by the kth user depends now on whether the kth user’s data bit changes or not during the observation interval, the kth signature altering its polarity at the moment t ¼ k in the second case. Suppose that the first user receiver knows the timings k of all users. In this case the number of potentially harmful MAI vectors created by K 1 side users is 2(K 1), unlike the synchronous case, where a similar number was only K 1. Together with the first signature vector we have 2K 1 vectors in total. If they are all linearly independent, a modified version of the decorrelating algorithm (10.13) may be used to eliminate MAI entirely regardless of the bits transmitted by users. Clearly, within the dimension (spreading factor) N, the maximal number of users K allowing such a processing is limited to 2K 1 N, i.e. cannot be greater than dN/2e. The necessary alteration of (10.13) is replacement of the ‘pure’ N K signature matrix A by an extended N (2K 1) one, whose columns are the first signature, K 1 properly time-shifted other signatures and the latter with polarity hops, starting at chip number zero (see Figure 7.15).
The MMSE detector interprets MAI statistically, i.e. as a random process described by its correlation matrix. The same interpretation is, certainly, applicable to the asynchronous case and again some revision is necessary to allow for changing the observation correlation matrix [19].
Since in an asynchronous system every side user bit may cover two consecutive bits of the user of interest, MAI correlation extends beyond the duration of one bit. That is the reason why the performance of asynchronous multiuser detectors typically improves when the observation interval spans several data bits.
We cannot go deeper into discussing multiuser detecting due to space limitations. This area is among the most challenging and rapidly advancing currently, and readers eager to get better insight into its current state as well as to learn about the prospects of its application in 3G and beyond are recommended to consult [19,100,102–104] and their references.
10.2 Multicarrier modulation and OFDM
In recent years the transmission mode called multicarrier (MC) modulation has gained great popularity in telecommunications. In general terms, MC modulation means no
Spread spectrum systems development |
317 |
|
|
more than involving a multitude of parallel subcarriers to transmit symbols of the same datastream. The specific form of utilizing the subcarriers may vary depending on the goal pursued. In our context the issue of primary interest is the relation of MC modulation with the spread spectrum concept. It follows from the previous contents that all advantages inherent to spread spectrum have their origin in a high time–frequency product (processing gain, spreading factor) WT. Various ways exist to widen the signal spectrum, given the duration given. DS spread spectrum solves this task, replacing conventional ‘slow’ symbol pulses by ‘fast’ signals of some convenient shape, i.e. controlling signal bandwidth via the time domain. MC modulation from this angle may be referred to as an alternative method of spreading the spectrum through its direct shaping in the frequency domain.
10.2.1 Multicarrier DS CDMA
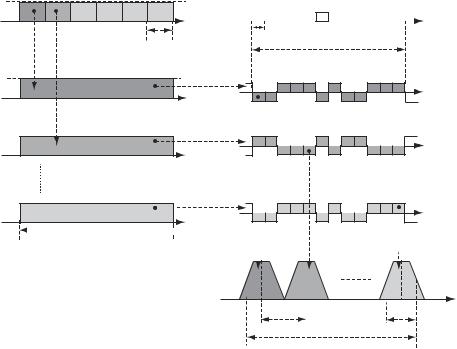
The simplest version of incorporating the MC technique into CDMA is an ordinary frequency multiplexing of data of the same user. To realize it Mc subcarriers transmit demultiplexed and DS spread data with non-overlapping spectra of subcarrier signals. Figure 10.2 explains this transmission mode, which is called multicarrier DS CDMA
Demultiplexing of source bit stream
Source (fast) bit stream
t
Tb
1st slow bit stream
t
2nd slow bit stream
t
Mcth slow bit stream









 t
t
Tb′ = McTb
|
|
|
|
|
|
DS signature |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆′ |
|
|
|
|
Tp′ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1st subcarrier spread symbol
t
2nd subcarrier spread symbol
t
Mcth subcarrier spread symbol
t
f1 |
f2 |
fMc |
f |
|
F |
W ′ |
|
|
|
W |
|
MC signal power spectrum
Figure 10.2 Explanation of MC-DS-CDMA

318 |
Spread Spectrum and CDMA |
|
|
(MC-DS-CDMA). The source ‘fast’ bit stream of rate R ¼ 1/Tb is demultiplexed (split) into Mc parallel ‘slow’ bit streams of rate R/Mc (or bit duration T 0b ¼ McTb) each. The ith slow bit stream is transmitted on its specific subcarrier of frequency fi, i ¼ 1, 2, . . . , Mc using DS spreading and some data modulation mode (BPSK, QPSK or other mode). With spreading chip duration D0 and subcarrier data symbol duration T 0p the bandwidth and spreading factor of one subcarrier signal are found as W0 1/D0 and N0 ¼ T 0p/D0 W 0T 0p, respectively. Spacing F of the subcarrier frequencies should exclude spectra overlapping, i.e. meet the restriction F ¼ W0 þ Fg, where Fg is a guard interval allowing for out-of-band spectra sidelobes. Therefore the total bandwidth occupied by the system:
W ¼ ðMc 1ÞF þ W0 ¼ McW0 þ ðMc 1ÞFg: |
ð10:26Þ |
The receiver of MC-DS-CDMA consists of Mc parallel identical receivers, each tuned on its own subcarrier and processing it independently of the others. Demodulated slow bit streams from their outputs are then multiplexed to restore the transmitted source fast bit stream.
Comparison of this system with DS CDMA of the same total bandwidth W and data rate R shows that due to the necessity for guard intervals MC-DS-CDMA yields to DS-CDMA in spreading factor. If both systems use the same modulation mode then symbol duration Tp for DS CDMA should be Mc times shorter than the MC-DS-CDMA symbol duration T 0p, but chip duration in DS CDMA may be taken as D 1/W providing the spreading factor N ¼ Tp/D WT 0p/Mc. In accordance with (10.26) the ratio of this entity to the spreading factor of MC-DS-CDMA:
N |
|
1 |
|
Mc 1 |
Fg |
|
1 |
ðMc 1ÞFg |
|
10:27 |
|
|
N0 |
¼ |
þ |
Mc W0 |
¼ |
þ W ðMc 1ÞFg |
ð |
Þ |
|||||
|
|
|
||||||||||
may remarkably exceed one. Since the spreading factor is the most important parameter of CDMA, determining user capacity, jamming immunity etc., MC-DS-CDMA proves to be not the best potential option for utilization of the available spectral resource. Sometimes, however, other factors may prevail, as takes place in the specification of cdma2000, which recommends MC-DS-CDMA for arranging a downlink on the grounds of backward compatibility with cdmaOne. In this case the single-carrier format of cdmaOne (slightly modified) is just replicated on three appropriately spaced carriers.
10.2.2 Conventional MC transmission and OFDM
Let us digress for a while from spread spectrum and CDMA to get a better understanding of the reasons underlying the considerable interest in the MC technique in modern wireless telecommunication. Suppose one wants to transmit a source bit stream using some conventional (non-spread-spectrum) modulation mode (BPSK, QPSK etc.). With M-ary modulation and necessary data transmission rate R, the duration of the data symbol pulse is Tp ¼ ( log2 M)/R. Suppose that the channel coherence bandwidth Bc (see Section 3.6) is significantly narrower than the bandwidth of data symbols (Bc W 1/Tp ¼ R/ log2 M), or, putting it differently, the delay spread ds exceeds symbol duration remarkably. Then under the ‘direct’ transmission (see Figure 10.3a),

Spread spectrum systems development |
|
|
|
319 |
Source (fast) bitstream |
|
Single carrier power spectrum |
|
|
|
|
|
|
|
(a) |
|
|
|
|
|
t |
f0 |
|
f |
Tb |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
1st slow bit stream |
|
W ≈ 1/Tp = |
|
|
|
|
log2 M |
|
|
|
t |
Subchannel power |
|
|
|
spectra |
|
|
|
|
|
|
|
|
2nd slow bit stream |
|
|
|
|
(b) |
|
|
|
|
|
t |
|
|
|
Mcth slow bit stream |
|
f1 f2 |
fMc |
f |
|
|
|
W ′ ≈ 1 |
|
|
|
F = W ′ |
|
|
|
t |
|
|
Tp′ |
Tb′ = McTb |
|
|
|
|
|
Overall MC spectrum |
|
||
|
|
|
||
|
|
|
|
f |
|
|
R |
|
|
|
|
W = McW ′ = |
|
|
|
|
log2 M |
|
|
Figure 10.3 Single-carrier (a) and MC (b) data transmission
a deep ISI (see Section 3.5.4) will be present, distorting the data symbols following the current one. To counter it the receiver will have to involve a rather complex equalizer with a long memory, typically realized as an adaptive FIR filter, i.e. tapped delay-line with adjustable tap weights.
MC transmission offers an alternative solution (Figure 10.3b) avoiding the need for complex equalizing. Let us again demultiplex the ‘fast’ source bit stream of rate R to Mc W/Bc parallel ‘slow’ bit streams having rate R/Mc each. Certainly, the overall rate provided by all slow bit streams is equal to the original one, i.e. R. Now let us take Mc subcarriers f1, f2, . . . , fMc spaced uniformly with interval F ¼ W0 ¼ W/Mc and use each of them to transmit one of Mc slow bit streams in the same modulation mode as before. Every individual subcarrier forms a separate subchannel operating regardless of the others and transmitting a slow bit stream by longer pulses (symbols) of duration Tp0 ¼ McTp, i.e. occupying Mc times narrower bandwidth W0 ¼ W/Mc than before. This means that within a subchannel the fading is no longer frequency-selective, since W0 ¼ W/Mc Bc. For a flat fading the delay spread does not go far beyond a single pulse, and ISI is less dramatic than it was initially and may be countered by comparatively simple equalizers. The total bandwidth occupied by the MC system is around W Mc/T 0p ¼ 1/Tp ¼ R/ log2 M, i.e. equalling that of the single-carrier transmission. In fact, spectral efficiency of the MC system appears to be even better, since the shape of its real spectrum is closer to a rectangle.

320 Spread Spectrum and CDMA
We do not use any frequency guard intervals now, and, moreover, allow subchannel spectra to overlap, since a traditional estimate of subchannel bandwidth W0 1/T 0p usually leaves remarkable out-of-band spectrum sidelobes. Nevertheless, the mutual interference between subchannels may be entirely suppressed. Suppose that the symbol
pulse is rectangular and by agreement its bandwidth |
is |
measured |
|
as W0 ¼ 1/T p0 . |
||
Then frequency spacing between adjacent subcarriers F |
¼ |
W0 |
¼ |
1/T |
p |
|
|
|
0 |
guarantees the |
|||
orthogonality of subchannel signals, i.e. complete elimination of mutual interference between the MC subchannels. That is why this version of the MC modulation technique bears the name orthogonal frequency division multiplexing (OFDM).
Let the modulation symbols (complex amplitudes) of Mc subcarriers of OFDM be bi ¼ Ai exp (j i), i ¼ 1, 2, . . . , Mc, where Ai and i are real amplitude and phase, respectively, and symbols are transmitted by rectangular pulses. Then the resulting signal in complex notation, which is physically a complex envelope to be up-converted further to
some central carrier f0, is: |
|
|
ð i Þ ¼ |
|
|
|
|
" |
|
|
ðTp0 |
# |
ð |
|
Þ |
|||
ð Þ ¼ i 1 |
i |
i 1 |
|
i |
|
|
|
|||||||||||
Mc |
b |
exp j2 f t |
|
Mc |
b exp j2 i 1Þt |
|
|
|
10:28 |
|
||||||||
S_ t |
|
|
X |
|
|
|
|
|||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
¼ |
|
|
¼ |
¼ |
|
|
¼ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
p |
|
|
|
|
|||||||
where f1 is set equal to zero, and therefore fi |
|
(i |
|
|
1)F |
|
|
(i |
|
1)/T 0 |
|
. The latter assump- |
||||||
tion leads to no loss of generality, since the eventual value of the central frequency is afterwards set up by an up-conversion. Signal (10.28) is OFDM symbol, the number of different OFDM symbols (OFDM alphabet size MOFDM) being determined by the size
of the alphabet of modulation symbols |
M and the number of |
frequencies: |
|||
MOFDM ¼ MMc . For the example of BPSK OFDM MOFDM ¼ 2Mc . |
|
||||
Sampling (10.28) with interval Ts ¼ T p0 /Mc produces the sequence: |
ð10:29Þ |
||||
S_l ¼ S_ðlT p0 =McÞ ¼ i 1 |
bi exp j2 ðMi c |
1Þl ; l ¼ 0; 1; . . . ; Mc 1 |
|||
Mc |
|
|
|
|
|
X |
|
|
|
|
|
¼
replicating (except for an immaterial constant coefficient) the inverse discrete Fourier transform (IDFT) of the sequence of modulation symbols fbig. This uncovers the key reason for the popularity of OFDM: to implement this MC mode there is no need to modulate parallel generators of Mc subcarriers and sum the results. The same output effect is obtained with the aid of IDFT of modulation symbols. Thus, the typical structure of an OFDM transmitter (Figure 10.4) includes demultiplexer, and an IDFT unit outputting the IDFT vector (10.29), which is then converted from parallel to serial form of sequential samples and interpolated to produce a continuous OFDM symbol
Fast stream
Demultiplexer
Slow streams
Parallel to
OFDM symbol
IDFT Interpolator
serial
Figure 10.4 Generation of OFDM symbol
Spread spectrum systems development |
321 |
|
|
(10.28). This latter (after introducing a prefix; see below) is up-converted and transmitted on the desired central frequency f0.
At the receiving end there is also no need to use Mc parallel receivers each tuned to its individual subcarrier, since one may extract fbig from (10.29) by the direct discrete Fourier transform (DDFT):
l 0 |
S_l exp j2 ðMi c |
1Þl |
¼ Mcbi; i ¼ 1; 2; . . . ; Mc |
ð10:30Þ |
||
Mc 1 |
|
|
|
|
|
|
X |
|
|
|
|
|
|
¼
This shows that a DDFT unit is an appropriate device to split a received OFDM symbol into Mc subchannel effects necessary to retrieve transmitted data. Still, at the real channel output the receiver does not have at its disposal a ‘pure’ OFDM symbol. Instead it observes a complex envelope Y_ (t), containing an OFDM symbol distorted by noise and ISI. As follows from its principle, the MC technique, increasing symbol duration limits the depth of ISI propagation to the symbol following the current one. To exclude this residual ISI, too, one may insert a guard interval of duration Tg ds between adjacent MC symbols. This interval should not compulsorily be empty. Moreover, filling it with a cyclic prefix of the OFDM symbol remarkably facilitates neutralization of the channel multipath effects. Appending a cyclic prefix serves to convert a convolution of the transmitted signal with the channel pulse response into the cyclic one, corresponding to the product of DFT images. Denote ¼ b ds/Tsc an integer number of sampling intervals in maximal channel delay and append v last samples of (10.29) as a prefix to the transmitted OFDM symbol. The receiver will drop
_ |
. . . , Mc 1, so that multipath replicas of the |
the first samples of Sl, l ¼ , þ 1, |
previous OFDM symbol will not affect Mc samples left. The delayed replicas of the current symbol itself will be influential, however, on the latter samples due to the
channel |
multipath propagation. |
|
If |
the |
channel |
pulse |
response |
samples are |
||||||||||
_ |
_ |
_ |
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
H0 |
, H1, . . . , H , then each observation sample Yl, l ¼ 0, 1, . . . , Mc 1 (noise neglected) |
|||||||||||||||||
is found as the convolution: |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
_ |
_ |
|
|
_ |
|
|
|
|
|
|
|
|
|
ð10:31Þ |
||
|
|
Yl ¼ |
|
Sl mHm; l ¼ 0; 1; . . . ; Mc 1 |
|
|||||||||||||
|
|
|
m¼0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Due to the cyclic prefix the sequence |
_ |
¼ 0, 1, . . . , Mc 1 is a cyclic shift of the |
||||||||||||||||
Sl m, l |
||||||||||||||||||
sequence |
_ |
|
. . . , |
|
, therefore (10.31) is a cyclic convolution, and its |
|||||||||||||
Sl for any m ¼ 0, 1, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
|
|
_ |
_ |
||
DFT spectrum is a product of DFTs |
_ |
|
_ |
of sequences |
||||||||||||||
Si and Hi |
Sl and Hl. DFT of the |
|||||||||||||||||
former is just a scaled sequence of modulation symbols fbig (see (10.30)), while |
||||||||||||||||||
|
|
H_ i |
¼ l |
|
0 |
H_ l exp |
|
|
ðMc |
1 |
Þ |
|
|
|
||||
|
|
~ |
|
X |
|
|
|
j2 i |
|
l |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¼
is the channel transfer function at the frequencies fi ¼ f1, f2, . . . , fMc , so that:
~ |
~ |
|
_ |
_ |
ð10:32Þ |
Yi ¼ McbiHi; i ¼ 1; 2; . . . ; Mc |
||
This result shows that to remove the channel influence on the OFDM signal, i.e. perform equalizing, it is enough to simply divide each sample at the output of the receiver DDFT
