Rc ¼ 1/2, df ¼ 5, so that Ga ¼ 2:5 or about 4 dB. We remember once again that Ga is derived for the AWGN channel (not BSC!); in other words, for the case of soft decoding. Hard decoding degrades this figure by 2–3 dB depending on code parameters and symbol SNR [31,33].

9.3.3 The Viterbi decoding algorithm

As was mentioned, among the reasons for the great popularity of convolutional codes the existence of a feasible decoding algorithm is of special importance. Let us begin with the following statement.

Proposition 9.3.1. The ML hard error-correction decoding of a binary code is equivalent to the minimum Hamming distance rule:

As one can see, the rule is very similar to (2.3) with a single change: in the case of BSC the Hamming distance replaces the Euclidean one, adequate for the AWGN channel. To prove (9.9) it is enough to note that (9.1) rewritten as:

is nothing but the BSC transition probability, i.e. the probability for the sent code vector u of length n being transformed by BSC into a binary observation y. Since the crossover probability of BSC p < 0:5, the transition probability p(yju) is a decreasing function of the Hamming distance from an observation y at the BSC output to a code vector u, and, therefore, the ML codeword u^ is the one closest to y by the Hamming distance.

A direct realization of (9.9) for an arbitrary code appeals to comparison of M Hamming distances from y to all codewords. Since M is typically quite large such a solution might appear infeasible. On the contrary, because of the beneficial structure of convolutional codes the ML decoding is not a big technological challenge, at least if the constraint length is moderate.

The Viterbi decoding procedure implements the ML strategy in a recurrent, step-by-step form of searching a path on the trellis diagram closest to the binary observation y. Every new decoding step starts with the arrival of the next group of n observation symbols. At the ith step the decoder calculates the distance of n incoming observation symbols from every branch of a trellis diagram and increments the distances for all paths calculated over the i 1 previous steps. One might work out the distances for an arbitrary code similarly, as new observation symbols arrive, but it is the recurrent nature of a convolutional code that makes this routine computationally economical due to the immediate discarding of many paths at each step.

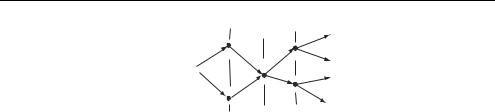
Figure 9.8 Paths going through node A at the ith step

Consider all paths passing through a fixed node A at the ith step, as shown in Figure 9.8. Continuation of any path after the ith step does not depend on the route of arriving at A, so that different paths reaching A may further merge with each other. But this means that of all the paths going through A and continuing the same way after the ith step the one having minimum distance from y up to the ith step will remain closest to y forever, since a common continuation adds an equal contribution to all distances! Why then go on with computing distances for the rest as soon as it is clear that they have no chance of finally appearing closest to the observation? Instead we discard them, retaining only the one reaching the node A with minimum distance. This latter is called a survivor and for the time being we believe that there is only a single survivor for every node of the trellis diagram at the ith step (see comments below). The current, i.e. calculated over all observed symbols up to the ith step, distance of the node A survivor from y is called the node metric of A.

Now recall that there are only two branches entering any node; Figure 9.8 shows this for some node A. Two branches enter it from two nodes B, C of the previous step and, therefore, continue the survivors of B and C. We may calculate the distances of two paths reaching A by just measuring the branch metrics, i.e. the distances of branches from the arriving group of n observed symbols, and adding them to the node metrics of B and C. The path with smaller distance is declared the survivor of A and is recorded in memory along with its distance (node metric) while the other is discarded. On performing these operations for all nodes of the trellis diagram the decoder proceeds to the next step.

To summarize briefly, the Viterbi decoder calculates branch metrics at every step, adds them to all the node metrics accumulated before and then sifts out the more distant of two paths leading to every node. Since there are 2 c 1 nodes (i.e. register states) altogether, the complexity of the decoder is determined only by the constraint length c and remains fixed independently of the theoretically unlimited number of codewords (paths).

Coming back to our assumption on the uniqueness of a survivor for every node, note that since Hamming distance is integer, the probability always exists that two paths leading to the same node have equal current distances from y. Different strategies are possible to solve ambiguity of this sort. One of them is just a random choice: assigning tails of a fair coin to one of the paths and declaring this one the survivor if tails really falls after flipping the coin. This certainly violates the decoding optimality, although the accompanying energy loss is typically insignificant. Alternatively, both competitive paths may be declared survivors and recorded in memory until further steps remove the ambiguity. The latter option preserves decoding optimality at the cost of involving extra memory.

c 1 ¼ 2 steps correspond to transient behaviour of the encoder register, when only one branch enters every state (see Figure 9.6) and so all paths are survivors. At the first step the decoder compares the first group of n ¼ 2 observation symbols with two branches emanating from the state (00). According to their Hamming distances from the observed symbol group 01, both the solid and dashed lines obtain metric 1, shown near the branches. Consequently, the node metrics of the two nodes, at which the branches arrive, both become equal to one. At the next step the distance is measured between the second group of observation symbols 00 and two pairs of branches emanating from nodes (00) and (10), resulting in the metrics labelling the branches. Added to the node metrics of the previous step, they update the metrics of nodes (00) and (10) and produce the metrics of two more nodes (01) and (11). Starting with the third step two branches enter any node of a trellis diagram of Figure 9.6, meaning that the decoder must decide which of them is a survivor. We do not show in Figure 9.9 the metrics of the branches beginning with this step in order to avoid clutter. As is seen, there are two paths leading to the node (00) at the third step. Their distances from the observed symbols 010011 are 3 and 2, respectively. The first is not a survivor and the decoder discards it along with its metric, so it is crossed out and not present at the plot of the next step. The second is a survivor, and is recorded in memory with its metric until the next step. In the same way, the decoder finds the survivors for the rest of the nodes. The decoding proceeds similarly at further steps, storing in memory only 2 c 1 ¼ 4 survivors, and every plot of Figure 9.9 depicts only the paths declared survivors at the previous step.

At step 7 the decoder first runs into the problem of ambiguity: two paths arrive at the node (01) with equal distances, and the same occurs with the node (11). The choice of survivors illustrated by the figure reflects some realization of flipping a fair coin. The same events happen at steps 8 and 9. The reader is encouraged (Problem 9.19) to make sure that any alternative resolving of the ambiguity will not change the final result of decoding except for the step number when the decoded bits are first released (see below).

The situation after the ninth step is very important: all paths appear to merge with each other up to the seventh symbol group. Whatever happens afterwards, this part of all merging paths will remain common forever, meaning that the data bits corresponding to it may be released right away as decoded ones. Hence, the decoder produces the decoded data 1000000. Comparing the codeword u ¼ 11101100000000 . . . corresponding to it with the observation y ¼ 0100110000 . . . we may note that the Hamming distance between them is 2, and if a transmitted word was really the one declared by the decoder, two errors were corrected, in full consistence with free distance df ¼ 5. Similar situations will arise at further steps, allowing the decoder to release decoded bits in the course of processing an observation symbol stream.

Certainly, outputting the decoded data at random moments of the merging of survivors, as in the example above, looks impractical, and a more regularly arranged procedure is desirable. It has been repeatedly verified by experiments and simulation that during the ith decoding step the merging part of all survivors almost never ends after the data bit number i 5 c, so the decision on every bit may be regularly output with delay 5 c [94].

A very significant feature of convolutional codes making them even more attractive is the comparative simplicity of implementing soft decoding. In a general case of a block code with M words the soft decoding means direct calculation of M Euclidean distances or correlations, no algebraic tricks like syndrome decoding being available. With a