
- •Contents
- •Preface
- •1 Spread spectrum signals and systems
- •1.1 Basic definition
- •1.2 Historical sketch
- •2 Classical reception problems and signal design
- •2.1 Gaussian channel, general reception problem and optimal decision rules
- •2.2 Binary data transmission (deterministic signals)
- •2.3 M-ary data transmission: deterministic signals
- •2.4 Complex envelope of a bandpass signal
- •2.5 M-ary data transmission: noncoherent signals
- •2.6 Trade-off between orthogonal-coding gain and bandwidth
- •2.7 Examples of orthogonal signal sets
- •2.7.1 Time-shift coding
- •2.7.2 Frequency-shift coding
- •2.7.3 Spread spectrum orthogonal coding
- •2.8 Signal parameter estimation
- •2.8.1 Problem statement and estimation rule
- •2.8.2 Estimation accuracy
- •2.9 Amplitude estimation
- •2.10 Phase estimation
- •2.11 Autocorrelation function and matched filter response
- •2.12 Estimation of the bandpass signal time delay
- •2.12.1 Estimation algorithm
- •2.12.2 Estimation accuracy
- •2.13 Estimation of carrier frequency
- •2.14 Simultaneous estimation of time delay and frequency
- •2.15 Signal resolution
- •2.16 Summary
- •Problems
- •Matlab-based problems
- •3 Merits of spread spectrum
- •3.1 Jamming immunity
- •3.1.1 Narrowband jammer
- •3.1.2 Barrage jammer
- •3.2 Low probability of detection
- •3.3 Signal structure secrecy
- •3.4 Electromagnetic compatibility
- •3.5 Propagation effects in wireless systems
- •3.5.1 Free-space propagation
- •3.5.2 Shadowing
- •3.5.3 Multipath fading
- •3.5.4 Performance analysis
- •3.6 Diversity
- •3.6.1 Combining modes
- •3.6.2 Arranging diversity branches
- •3.7 Multipath diversity and RAKE receiver
- •Problems
- •Matlab-based problems
- •4 Multiuser environment: code division multiple access
- •4.1 Multiuser systems and the multiple access problem
- •4.2 Frequency division multiple access
- •4.3 Time division multiple access
- •4.4 Synchronous code division multiple access
- •4.5 Asynchronous CDMA
- •4.6 Asynchronous CDMA in the cellular networks
- •4.6.1 The resource reuse problem and cellular systems
- •4.6.2 Number of users per cell in asynchronous CDMA
- •Problems
- •Matlab-based problems
- •5 Discrete spread spectrum signals
- •5.1 Spread spectrum modulation
- •5.2 General model and categorization of discrete signals
- •5.3 Correlation functions of APSK signals
- •5.4 Calculating correlation functions of code sequences
- •5.5 Correlation functions of FSK signals
- •5.6 Processing gain of discrete signals
- •Problems
- •Matlab-based problems
- •6 Spread spectrum signals for time measurement, synchronization and time-resolution
- •6.1 Demands on ACF: revisited
- •6.2 Signals with continuous frequency modulation
- •6.3 Criterion of good aperiodic ACF of APSK signals
- •6.4 Optimization of aperiodic PSK signals
- •6.5 Perfect periodic ACF: minimax binary sequences
- •6.6 Initial knowledge on finite fields and linear sequences
- •6.6.1 Definition of a finite field
- •6.6.2 Linear sequences over finite fields
- •6.6.3 m-sequences
- •6.7 Periodic ACF of m-sequences
- •6.8 More about finite fields
- •6.9 Legendre sequences
- •6.10 Binary codes with good aperiodic ACF: revisited
- •6.11 Sequences with perfect periodic ACF
- •6.11.1 Binary non-antipodal sequences
- •6.11.2 Polyphase codes
- •6.11.3 Ternary sequences
- •6.12 Suppression of sidelobes along the delay axis
- •6.12.1 Sidelobe suppression filter
- •6.12.2 SNR loss calculation
- •6.13 FSK signals with optimal aperiodic ACF
- •Problems
- •Matlab-based problems
- •7 Spread spectrum signature ensembles for CDMA applications
- •7.1 Data transmission via spread spectrum
- •7.1.1 Direct sequence spreading: BPSK data modulation and binary signatures
- •7.1.2 DS spreading: general case
- •7.1.3 Frequency hopping spreading
- •7.2 Designing signature ensembles for synchronous DS CDMA
- •7.2.1 Problem formulation
- •7.2.2 Optimizing signature sets in minimum distance
- •7.2.3 Welch-bound sequences
- •7.3 Approaches to designing signature ensembles for asynchronous DS CDMA
- •7.4 Time-offset signatures for asynchronous CDMA
- •7.5 Examples of minimax signature ensembles
- •7.5.1 Frequency-offset binary m-sequences
- •7.5.2 Gold sets
- •7.5.3 Kasami sets and their extensions
- •7.5.4 Kamaletdinov ensembles
- •Problems
- •Matlab-based problems
- •8 DS spread spectrum signal acquisition and tracking
- •8.1 Acquisition and tracking procedures
- •8.2 Serial search
- •8.2.1 Algorithm model
- •8.2.2 Probability of correct acquisition and average number of steps
- •8.2.3 Minimizing average acquisition time
- •8.3 Acquisition acceleration techniques
- •8.3.1 Problem statement
- •8.3.2 Sequential cell examining
- •8.3.3 Serial-parallel search
- •8.3.4 Rapid acquisition sequences
- •8.4 Code tracking
- •8.4.1 Delay estimation by tracking
- •8.4.2 Early–late DLL discriminators
- •8.4.3 DLL noise performance
- •Problems
- •Matlab-based problems
- •9 Channel coding in spread spectrum systems
- •9.1 Preliminary notes and terminology
- •9.2 Error-detecting block codes
- •9.2.1 Binary block codes and detection capability
- •9.2.2 Linear codes and their polynomial representation
- •9.2.3 Syndrome calculation and error detection
- •9.2.4 Choice of generator polynomials for CRC
- •9.3 Convolutional codes
- •9.3.1 Convolutional encoder
- •9.3.2 Trellis diagram, free distance and asymptotic coding gain
- •9.3.3 The Viterbi decoding algorithm
- •9.3.4 Applications
- •9.4 Turbo codes
- •9.4.1 Turbo encoders
- •9.4.2 Iterative decoding
- •9.4.3 Performance
- •9.4.4 Applications
- •9.5 Channel interleaving
- •Problems
- •Matlab-based problems
- •10 Some advancements in spread spectrum systems development
- •10.1 Multiuser reception and suppressing MAI
- •10.1.1 Optimal (ML) multiuser rule for synchronous CDMA
- •10.1.2 Decorrelating algorithm
- •10.1.3 Minimum mean-square error detection
- •10.1.4 Blind MMSE detector
- •10.1.5 Interference cancellation
- •10.1.6 Asynchronous multiuser detectors
- •10.2 Multicarrier modulation and OFDM
- •10.2.1 Multicarrier DS CDMA
- •10.2.2 Conventional MC transmission and OFDM
- •10.2.3 Multicarrier CDMA
- •10.2.4 Applications
- •10.3 Transmit diversity and space–time coding in CDMA systems
- •10.3.1 Transmit diversity and the space–time coding problem
- •10.3.2 Efficiency of transmit diversity
- •10.3.3 Time-switched space–time code
- •10.3.4 Alamouti space–time code
- •10.3.5 Transmit diversity in spread spectrum applications
- •Problems
- •Matlab-based problems
- •11 Examples of operational wireless spread spectrum systems
- •11.1 Preliminary remarks
- •11.2 Global positioning system
- •11.2.1 General system principles and architecture
- •11.2.2 GPS ranging signals
- •11.2.3 Signal processing
- •11.2.4 Accuracy
- •11.2.5 GLONASS and GNSS
- •11.2.6 Applications
- •11.3 Air interfaces cdmaOne (IS-95) and cdma2000
- •11.3.1 Introductory remarks
- •11.3.2 Spreading codes of IS-95
- •11.3.3 Forward link channels of IS-95
- •11.3.3.1 Pilot channel
- •11.3.3.2 Synchronization channel
- •11.3.3.3 Paging channels
- •11.3.3.4 Traffic channels
- •11.3.3.5 Forward link modulation
- •11.3.3.6 MS processing of forward link signal
- •11.3.4 Reverse link of IS-95
- •11.3.4.1 Reverse link traffic channel
- •11.3.4.2 Access channel
- •11.3.4.3 Reverse link modulation
- •11.3.5 Evolution of air interface cdmaOne to cdma2000
- •11.4 Air interface UMTS
- •11.4.1 Preliminaries
- •11.4.2 Types of UMTS channels
- •11.4.3 Dedicated physical uplink channels
- •11.4.4 Common physical uplink channels
- •11.4.5 Uplink channelization codes
- •11.4.6 Uplink scrambling
- •11.4.7 Mapping downlink transport channels to physical channels
- •11.4.8 Downlink physical channels format
- •11.4.9 Downlink channelization codes
- •11.4.10 Downlink scrambling codes
- •11.4.11 Synchronization channel
- •11.4.11.1 General structure
- •11.4.11.2 Primary synchronization code
- •11.4.11.3 Secondary synchronization code
- •References
- •Index

Spread spectrum signature ensembles |
|
|
|
243 |
|
|
|
||
the sequence fig ¼ f. . . , 0, 1, 2, 0, 1, 2, . . .g they give K ¼ p 1 ¼ 2 |
sequences |
of period |
||
L ¼ p(p þ 1) ¼ 12: f1, 2, 1, 2, 2, 0, 2, 0, 0, 1, 0, 1g and |
f0, 0, 2, 1, 1, 1, 0, 2, 2, 2, 1, 0g. |
The last |
||
step, replacement of their elements by extended |
characters |
(0) ¼ |
(1) ¼ þ1, |
(2) ¼ 1, |
produces the Kamaletdinov set of two binary |
sequences |
of length L ¼ 12: fa1, i g ¼ |
||
fþ þ þ þ þ þ þþg and fa2, i g ¼ fþ þ þ þ þ þ þþg. Their ACF and CCF are not difficult to compute by hand (or with the aid of the program of Problem 7.43), coming to 2max ¼ 1/9 in full agreement with (7.61).
Table 7.1 Examples of binary minimax signature sets
Ensemble |
|
|
|
|
|
Length L |
|
|
|
Size K |
|
|
Squared correlation |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
peak 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
||
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
2 |
! |
|
|
||||
Gold |
|
|
1, n |
|
0 mod4 |
L |
|
2 |
|
|
|
|
1 |
(p2(Lþ1)þ1)2 |
|
|
|
2 |
|
|||||||||
|
|
|
|
|
6¼ |
|
|
þ |
|
|
¼ |
|
|
þ |
|
L2 |
|
|
! |
L |
, n odd |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2p(L |
þ þ |
|
|
|
|
|
|||
|
7,31,63,127,511,1023 |
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
L |
, n even |
||||||||||||
|
15,63,255,1023 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Kasami |
2n |
|
|
1, n even |
|
pL |
þ |
1 |
|
|
|
|
|
(pLþ1þ1) |
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
! L |
|
|
||||||||
bent sequences |
15,255 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Union of Kasami and |
2n |
|
|
1, n |
|
0 mod4 |
2pL |
|
|
1 |
|
1 |
|
(pLþ1þ1)2 |
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
¼ |
|
|
|
|
|
þ |
|
|
|
|
|
L2 |
|
! L |
|
|
|||||||
|
42,110,342,506,930 |
! pL |
|
p |
|
1)2 |
|
! |
|
|
|
|
|
|
|
|||||||||||||
Kamaletdinov 1 |
p(p |
|
1), (p |
¼ |
3 mod4, prime) |
p |
þ |
1 |
¼ |
p |
|
|
(p 3)2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
L |
|
|
L |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
4Lþ1þ3 |
þ2 |
|
|
1 |
|
|
|
|
|
|
|||||||||||
Kamaletdinov 2 |
p(p |
|
|
1), (p |
|
3 mod4, prime) |
p |
|
1 |
|
|
4Lþ1 3 |
(pþ2 |
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
12,56,132,380,552,992 |
|
pL |
|
|
|
|
L |
|
! L |
|
|
|
|
|
|
||||||||||||
|
|
|
þ |
|
|
¼ |
|
|
|
|
|
¼ |
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
To prove the propositions on the correlation peak of the ensembles above, the theory of quadratic equations in finite fields is necessary. Leaving this sophisticated issue aside, we refer the interested reader to the original paper [76].
Let us summarize now our knowledge on the binary minimax ensembles in Table 7.1, presenting length (listing all the lengths of existing ensembles within the range 7 L 1023), number of signatures and squared correlation. The table is expressive enough as regards the significant contribution of Kamaletdinov sets: the number of their lengths in the considered range is 11, compared to 6 for Gold and 4 for Kasami sets.
Problems
7.1.In a DS CDMA system based on periodic binary signatures and BPSK data modulation, a user transmits the signal fþ þ þ þ þ þ þ þ þ þ g covering more than two data bits. What is the signature code of this user (the common sign of all symbols being immaterial) if data bit duration equals signature period?
7.2.In a DS CDMA system based on periodic binary signatures and BPSK data modulation, a user employs the signature code fþ þ þ þ g, data bit duration
244 |
Spread Spectrum and CDMA |
|
|
being equal to the signature period 7D. Due to the failure of timing recovery in the receiver, the despreading reference lags behind the received spreading signal by one chip. What is the result of data demodulation when a stream of zero data bits is transmitted?
7.3.How will the presence of amplitude modulation in an APSK signature affect the structure of a DS spreading receiver? Will the despreading in this case return a data symbol to the form characteristic of a non-spread transmission?
7.4.A DS CDMA system uses QPSK for data transmission at the rate 64 kbps and spreading code with chip rate 1.28 megachips per second (Mcps). Find the spreading factor and bandwidth occupied by the system.
7.5. |
An |
FH |
CDMA |
system |
uses |
a |
4-frequency |
spreading |
signal |
of |
length |
|
N ¼ 4: f1, 4, 2, 3g and 4-FSK data transmission (each couple of bits is transmitted |
||||||||||
|
by one of 4 frequencies). The transmitted bit stream is 00101101. Draw a possible |
||||||||||
|
time–frequency array of the transmitted signal if one data bit covers two chip |
||||||||||
|
durations. What sort of FH is used: fast or slow? |
|
|
|
|
||||||
7.6. |
An |
FH |
CDMA |
system |
uses |
a |
4-frequency |
spreading |
signal |
of |
length |
N ¼ 4: f1, 4, 2, 3g and 4-FSK data transmission (each couple of bits is transmitted by one of 4 frequencies). The transmitted bit stream is 10110100. Draw a possible time–frequency array of the transmitted signal if one signature chip covers two data bits. What sort of FH is used: fast or slow?
7.7.A fast FH CDMA system uses 16-frequency spreading signal and 4-FSK data modulation. The chip duration is 10 ms. Estimate the minimal bandwidths of spreading and transmitted signals if chips of different frequencies should be orthogonal.
7.8. A synchronous CDMA system with BPSK data transmission at the rate R ¼ 9:6 kbps should be organized within an available bandwidth Wt ¼ 76:8 kHz. How many users can it accommodate to preserve the optimality of a single-user receiver? Design an appropriate binary signature set. How will the number of users change if BPSK data transmission is replaced by QPSK, 8-PSK or 16-QAM? If any of them increases the number of users, at what cost does this happen?
7.9.A synchronous CDMA system serves 36 users employing orthogonal signatures of equal energy per bit. How many new signatures (bandwidth and user data rate being fixed) of the same bit energy can one add to the existing ones without sacrificing minimum distance between different group signals?
7.10.What is the minimum length of synchronous signatures allowing a no smaller than 33% increase of the number of users in the oversaturation scheme (7.23)?
7.11.Add a supplementary signature to the four Walsh functions of length N ¼ 4. Is the supplementary signature binary? If not, can you modify the primary signatures to make the supplementary one binary?
7.12.K ¼ (4N 1)/3 synchronous signatures are built according to the oversaturation scheme (7.23). Is it a good idea to use them for a K-user CDMA, if only a singleuser receiver is acceptable?
7.13.Find the minimal length potentially allowing MAI power per signature per conventional receiver in a synchronous oversaturated CDMA no higher than 30 dB relative to the useful signal power, if the number of users is 101.
7.14.Prove that three or more binary sequences of length N cannot be orthogonal to each other unless their length is a multiple of four.

Spread spectrum signature ensembles |
245 |
|
|
7.15.Can an oversaturated Welch-bound set of K ¼ 21 binary signatures exist? What about K ¼ 22, 23 or 32?
7.16.Outline the procedure of building a Welch-bound set of K ¼ 256 binary sequences of length N ¼ 100.
7.17.(Karystinos and Pados [64].) Prove that for an oversaturated set of an odd number K of binary signatures, the Welch bound (7.30) rises to:
TSC K2 þ N 1
N N
7.18. Build an ensemble of K ¼ 15 binary signatures of length N ¼ 12 achieving the bound of the previous problem. Generalize the procedure to K ¼ 2m 1 signatures (K > N).
7.19. What is the minimum period of K ¼ 11 asynchronous signatures which does not prohibit obtaining average squared correlation between all their cyclic replicas within 20 dB?
7.20. Consider random signatures meeting (7.37). Prove that multiplication of signatures by data symbols (data modulation) does not disturb (7.37), provided data symbols are independent of signature symbols.
7.21. Prove that if two sequences of the same least period L both have perfect periodic ACF, their periodic CCF cannot equal zero for all mutual shifts.
7.22. Find the maximal number of asynchronous signatures of the period L ¼ 100 which does not prohibit retaining the correlation peak below 23 dB.
7.23. K ¼ 50 users may move freely within a zone of radius Dc ¼ 15 km. The maximal delay spread of the channel between a user and central station ds ¼ 20 ms. Bandwidth allocated to the system is 2 MHz. Find the minimum lengths of the binary m-sequence and Legendre sequence allowing arranging time-offset signatures for the link ‘user–central station’. Find the minimal length of the perfect PACF ternary sequence of memory 3 matching this problem.
7.24. In Section 7.5.1 an m-sequence is used to generate a frequency-offset signature set. Does any other binary minimax sequence (e.g. a Legendre one) allow the same way of obtaining a signature set with squared correlation peak around 1/L? If not, why?
7.25. A CDMA system operates at carrier wavelength 4 cm with signature chip duration 1 ms. The length of signatures should be L ¼ 210 1 ¼ 1023. What maximal number of frequency-offset signatures may be arranged, if the user’s velocity ranges up to 144 km/h?
7.26. Find all decimation indexes fitting the Gold algorithm for lengths 63, 127, 511, 1023.
7.27. A signature ensemble is necessary to serve K ¼ 100 users with correlation peak no greater than 0.064. What is the minimal length of the Gold ensemble meeting these demands?
7.28. Prove the minimax property (7.56) of Kasami sets.
7.29. A signature ensemble is necessary of size no smaller than 31 with correlation peak below 23 dB. Find the ensemble of minimal length among the known binary ones matching this requirement.

246 |
Spread Spectrum and CDMA |
|
|
7.30.A signature ensemble is necessary of size no smaller than 24 with correlation peak below 25 dB. Find the ensemble of minimal length among the known binary ones matching this requirement.
Matlab-based problems
7.31.Write a program illustrating the principle of DS spreading–despreading (see Figures 7.3 and 7.4).
7.32.Figure 7.20 illustrates Matlab simulation of fast FH spreading using the example of 6 chips per one bit duration, the 4-frequency signature fFig ¼ (1, 3, 2, 1, 0, 3) and binary FSK data modulation (frequency offset of bit one fd ¼ 4). Write a program simulating fast FH spreading–despreading for a range of parameters.
|
1.0 |
|
|
|
|
|
|
B(t) |
0.5 |
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
|
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
|
3 |
|
|
|
|
|
|
t) |
2 |
|
|
|
|
|
|
Fs( |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
) |
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
|
|
|
|
|
|
|
|
Fs(t |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
4 |
|
|
|
|
|
|
(t) |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
fd*B |
|
|
|
|
|
|
|
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
|
|
0 |
||||||
|
1 |
|
|
|
|
|
|
(t) |
0 |
|
|
|
|
|
|
St |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
|
|
|
|
t/Tb |
|
|
|
Figure 7.20 Fast FH spreading
7.33.Write a program calculating the squared distance between two group signals (7.11) using equation (7.15) for an arbitrary given synchronous signature set and binary data transmission. Test it for an orthogonal signature set (e.g. Hadamard matrix rows), varying randomly the patterns of differences "k.
7.34.Modify the program of the previous problem to calculate the minimum squared distance in a constellation of group signals (7.11) for an arbitrary set of K synchronous signatures and binary data transmission. Up to which set sizes K does the program run in a reasonable time?
7.35.Write a program generating an oversaturated signature set according to the scheme (7.23) for lengths N ¼ 4l with arbitrary l. Take the lth Kronecker degree
of H4 from Example 7.2.1 as the primary signatures. Make sure that all the
Spread spectrum signature ensembles |
247 |
|
|
supplementary signatures are binary. Use the program of Problem 7.33 for a spot check of the distances between group signals.
7.36.Write a program simulating multiuser reception in oversaturated synchronous CDMA. Steps to be done:
(a)Form K ¼ 21 binary signatures as in the previous problem.
(b)Form a random K-dimensional vector of bits transmitted by K users.
(c)Modulate the signatures by bits in the BPSK manner and form a group signal.
(d)Add the Gaussian noise to the group signal, setting the noise standard deviation to something like the signature amplitude.
(e)Plot the observation obtained.
(f)Try all possible 2K bit patterns, each time forming a candidate group signal and measuring the Euclidean distance from it to the received observation.
(g)Give out the decision on the bit pattern providing the closest candidate group signal to the observation and check whether all bit decisions are correct.
(h)Run the program, increasing the noise level, and comment on the results.
7.37.Write a program computing total squared correlation and average squared correlation per signature pair for an arbitrary synchronous signature set.
7.38.Write a program constructing an oversaturated binary Welch-bound set of K ¼ 2n signatures of arbitrary length N < K. Use the set obtained in simulating K-user synchronous CDMA. Steps to be done:
(a)Construct a Hadamard matrix of size K.
(b)Discard N K rows in it and use the columns of the truncated matrix as signatures.
(c)Form the K-dimensional vector of users’ data, and use it to manipulate signatures and form a group signal.
(d)Simulate K single-user receivers, each calculating the correlation of the received group signal with an appropriate signature and taking the decision according to the polarity of the correlation.
(e)Compare the K-dimensional vector of decisions on the data with the one really transmitted and find the number of erroneous bits.
(f)Repeat items (c)–(e) 1000–10 000 times and find the bit error probability per user.
(g)Run the program for n ¼ 5, 6, 7, 8 finding each time the minimal length N (maximal oversaturation K/N) where errors do not still occur.
7.39.Write a program simulating an asynchronous CDMA employing time-offset replicas of the same binary m-sequence. Recommended steps:
(a)Set the maximal number of users K ¼ 20 25 and the maximal delay in number of chips mmax ¼ 80 100.
(b)Form the binary f 1g m-sequence of length L K(mmax þ 1).
(c)Take as K signatures K cyclic replicas of the m-sequences, each delayed from the previous by mmax þ 1.
(d)Pick out Ka first signatures (active users) and manipulate all but the first by random independent bits, bit duration fixed within N ¼ 160 200 chips.
248 |
Spread Spectrum and CDMA |
|
|
(e)Shift all manipulated signatures but the first randomly and independently versus their initial versions within the range [0, mmax] and add their sum to the first signature to come to a group signal.
(f)Imitate a single-user receiver for the first user, calculating the correlation within one bit of the first signature and the group signal.
(g)Demodulate the first user bit and compare it to the true one (which is zero).
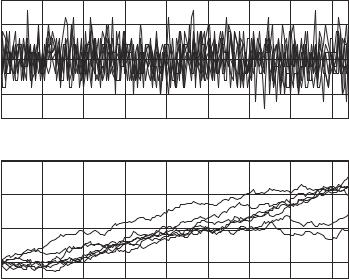
(h)Varying the number of active users, e.g. Ka ¼ 5, 10, 20, . . . repeat items (d)–(g) 1000–5000 times for every Ka. Calculate an experimental floor SIR at the correlator output and the bit error probability and compare them with the predictions q2I ¼ N/(K 1), Pe ¼ Q(qI ).
(i)Plot 5–7 overlapped example realizations of a group signal and cumulative sum at the receiver integrator output (Figure 7.21 presents example plots for K ¼ 25, Ka ¼ 20, N ¼ 169, mmax ¼ 80).
signal |
10 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Group |
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
|
300 |
|
|
|
|
|
|
|
|
Correlation |
200 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
|
|
|
|
|
t/∆ |
|
|
|
|
Figure 7.21 Group signal and receiver integrator output in asynchronous CDMA
7.40.Write a program generating the Gold set and outputting the histogram of the values of the periodic ACF and CCF of its members. Figure 7.22 presents example plots for N ¼ 25 1.
(a)Generate a binary m-sequence of a proper memory n 5.
(b)Decimate it in an appropriate manner to come to the second initial m-sequence.
(c)Form 15–20 Gold sequences as prescribed by (7.52), including initial
m-sequences.

Spread spectrum signature ensembles |
249 |
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
Ra(τ) |
20 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
τ |
|
|
0 |
|
5 |
10 |
|
15 |
|
20 |
25 |
30 |
|
|
30 |
|
|
|
|
|
|
|
|
|
|
Ra(τ) |
20 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
5 |
10 |
|
15 |
|
20 |
25 |
τ |
30 |
|
0 |
|
|
|
|||||||
|
30 |
|
|
|
|
|
|
|
|
|
|
Rc(τ) |
20 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
τ |
|
|
0 |
|
5 |
10 |
|
15 |
|
20 |
25 |
30 |
|
Rc(τ) |
30 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
τ |
|
|
0 |
|
5 |
10 |
|
15 |
|
20 |
25 |
30 |
|
Occurences |
5000 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
–8 |
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
8 |
10 |
|
|
–10 |
||||||||||
|
|
|
|
|
|
Correlation |
|
|
|
|
|
Figure 7.22 Periodic correlations and histogram of correlations for the Gold set of length 31
(d)Calculate their periodic ACF and CCF.
(e)Plot ACF of one of the initial m-sequences, ACF of some other Gold sequence, CCF of two initial m-sequences, and CCF of another pair out of the Gold sequences obtained.
(f)Plot a histogram of all unwanted correlations (CCF values and ACF sidelobes).
(g)Output the correlation peak and compare it with the theoretically predicted one and the lower bound.
(h)Run the program for relevant odd and even values n and interpret the results.
7.41.Write a program to investigate Kasami sets. The procedure may be in general similar to that of the previous problem, but now it makes sense to calculate the correlations between all (not only selected) sequences.
7.42.Write a program to investigate Kamaletdinov sets determined by (7.57)–(7.58). Figure 7.23 present the plots for the case p ¼ 11. Recommended steps:
(a)Set p ¼ 3 mod4, find a primitive element in GF(p) and its inverse 1.
(b)Form K ¼ p þ 1 sequences over GF(p) as defined by (7.57), all arithmetic being of GF(p).
(c)Map the sequences obtained onto the binary f 1g alphabet according to
(7.58).

250 |
Spread Spectrum and CDMA |
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
τ) |
50 |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
Ra |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
(τ) |
50 |
|
|
|
|
|
|
|
|
|
|
|
Ra |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
Rc(τ) Rc(τ)
100
50
0
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
100
50
0
Occurences
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
10000
5000
0
–15 |
–10 |
–5 |
0 |
5 |
10 |
15 |
|
|
|
Correlation |
|
|
|
Figure 7.23 Periodic correlations and histogram of correlations for Kamaletdinov set of length 110
(d)Calculate the periodic ACF and CCF of all the sequences of the previous item.
(e)Plot ACF of sequences faK, ig and fa1, ig.
(f)Plot CCF of this pair and pair faK 1, ig, faK, ig.
(g)Plot a histogram of all unwanted correlations (CCF values and ACF sidelobes).
(h)Output the correlation peak and compare it with the theoretically predicted one and the lower bound.
(i)Run the program, varying p, and interpret the results.
7.43.Write a program to investigate Kamaletdinov sets determined by (7.60). Run it varying p, plot selected periodic ACF, CCF, and histograms of unwanted correlations. Register the correlation peak, and compare it to the theoretically predicted
one and to the lower bound.
