
- •Contents
- •Preface
- •1 Spread spectrum signals and systems
- •1.1 Basic definition
- •1.2 Historical sketch
- •2 Classical reception problems and signal design
- •2.1 Gaussian channel, general reception problem and optimal decision rules
- •2.2 Binary data transmission (deterministic signals)
- •2.3 M-ary data transmission: deterministic signals
- •2.4 Complex envelope of a bandpass signal
- •2.5 M-ary data transmission: noncoherent signals
- •2.6 Trade-off between orthogonal-coding gain and bandwidth
- •2.7 Examples of orthogonal signal sets
- •2.7.1 Time-shift coding
- •2.7.2 Frequency-shift coding
- •2.7.3 Spread spectrum orthogonal coding
- •2.8 Signal parameter estimation
- •2.8.1 Problem statement and estimation rule
- •2.8.2 Estimation accuracy
- •2.9 Amplitude estimation
- •2.10 Phase estimation
- •2.11 Autocorrelation function and matched filter response
- •2.12 Estimation of the bandpass signal time delay
- •2.12.1 Estimation algorithm
- •2.12.2 Estimation accuracy
- •2.13 Estimation of carrier frequency
- •2.14 Simultaneous estimation of time delay and frequency
- •2.15 Signal resolution
- •2.16 Summary
- •Problems
- •Matlab-based problems
- •3 Merits of spread spectrum
- •3.1 Jamming immunity
- •3.1.1 Narrowband jammer
- •3.1.2 Barrage jammer
- •3.2 Low probability of detection
- •3.3 Signal structure secrecy
- •3.4 Electromagnetic compatibility
- •3.5 Propagation effects in wireless systems
- •3.5.1 Free-space propagation
- •3.5.2 Shadowing
- •3.5.3 Multipath fading
- •3.5.4 Performance analysis
- •3.6 Diversity
- •3.6.1 Combining modes
- •3.6.2 Arranging diversity branches
- •3.7 Multipath diversity and RAKE receiver
- •Problems
- •Matlab-based problems
- •4 Multiuser environment: code division multiple access
- •4.1 Multiuser systems and the multiple access problem
- •4.2 Frequency division multiple access
- •4.3 Time division multiple access
- •4.4 Synchronous code division multiple access
- •4.5 Asynchronous CDMA
- •4.6 Asynchronous CDMA in the cellular networks
- •4.6.1 The resource reuse problem and cellular systems
- •4.6.2 Number of users per cell in asynchronous CDMA
- •Problems
- •Matlab-based problems
- •5 Discrete spread spectrum signals
- •5.1 Spread spectrum modulation
- •5.2 General model and categorization of discrete signals
- •5.3 Correlation functions of APSK signals
- •5.4 Calculating correlation functions of code sequences
- •5.5 Correlation functions of FSK signals
- •5.6 Processing gain of discrete signals
- •Problems
- •Matlab-based problems
- •6 Spread spectrum signals for time measurement, synchronization and time-resolution
- •6.1 Demands on ACF: revisited
- •6.2 Signals with continuous frequency modulation
- •6.3 Criterion of good aperiodic ACF of APSK signals
- •6.4 Optimization of aperiodic PSK signals
- •6.5 Perfect periodic ACF: minimax binary sequences
- •6.6 Initial knowledge on finite fields and linear sequences
- •6.6.1 Definition of a finite field
- •6.6.2 Linear sequences over finite fields
- •6.6.3 m-sequences
- •6.7 Periodic ACF of m-sequences
- •6.8 More about finite fields
- •6.9 Legendre sequences
- •6.10 Binary codes with good aperiodic ACF: revisited
- •6.11 Sequences with perfect periodic ACF
- •6.11.1 Binary non-antipodal sequences
- •6.11.2 Polyphase codes
- •6.11.3 Ternary sequences
- •6.12 Suppression of sidelobes along the delay axis
- •6.12.1 Sidelobe suppression filter
- •6.12.2 SNR loss calculation
- •6.13 FSK signals with optimal aperiodic ACF
- •Problems
- •Matlab-based problems
- •7 Spread spectrum signature ensembles for CDMA applications
- •7.1 Data transmission via spread spectrum
- •7.1.1 Direct sequence spreading: BPSK data modulation and binary signatures
- •7.1.2 DS spreading: general case
- •7.1.3 Frequency hopping spreading
- •7.2 Designing signature ensembles for synchronous DS CDMA
- •7.2.1 Problem formulation
- •7.2.2 Optimizing signature sets in minimum distance
- •7.2.3 Welch-bound sequences
- •7.3 Approaches to designing signature ensembles for asynchronous DS CDMA
- •7.4 Time-offset signatures for asynchronous CDMA
- •7.5 Examples of minimax signature ensembles
- •7.5.1 Frequency-offset binary m-sequences
- •7.5.2 Gold sets
- •7.5.3 Kasami sets and their extensions
- •7.5.4 Kamaletdinov ensembles
- •Problems
- •Matlab-based problems
- •8 DS spread spectrum signal acquisition and tracking
- •8.1 Acquisition and tracking procedures
- •8.2 Serial search
- •8.2.1 Algorithm model
- •8.2.2 Probability of correct acquisition and average number of steps
- •8.2.3 Minimizing average acquisition time
- •8.3 Acquisition acceleration techniques
- •8.3.1 Problem statement
- •8.3.2 Sequential cell examining
- •8.3.3 Serial-parallel search
- •8.3.4 Rapid acquisition sequences
- •8.4 Code tracking
- •8.4.1 Delay estimation by tracking
- •8.4.2 Early–late DLL discriminators
- •8.4.3 DLL noise performance
- •Problems
- •Matlab-based problems
- •9 Channel coding in spread spectrum systems
- •9.1 Preliminary notes and terminology
- •9.2 Error-detecting block codes
- •9.2.1 Binary block codes and detection capability
- •9.2.2 Linear codes and their polynomial representation
- •9.2.3 Syndrome calculation and error detection
- •9.2.4 Choice of generator polynomials for CRC
- •9.3 Convolutional codes
- •9.3.1 Convolutional encoder
- •9.3.2 Trellis diagram, free distance and asymptotic coding gain
- •9.3.3 The Viterbi decoding algorithm
- •9.3.4 Applications
- •9.4 Turbo codes
- •9.4.1 Turbo encoders
- •9.4.2 Iterative decoding
- •9.4.3 Performance
- •9.4.4 Applications
- •9.5 Channel interleaving
- •Problems
- •Matlab-based problems
- •10 Some advancements in spread spectrum systems development
- •10.1 Multiuser reception and suppressing MAI
- •10.1.1 Optimal (ML) multiuser rule for synchronous CDMA
- •10.1.2 Decorrelating algorithm
- •10.1.3 Minimum mean-square error detection
- •10.1.4 Blind MMSE detector
- •10.1.5 Interference cancellation
- •10.1.6 Asynchronous multiuser detectors
- •10.2 Multicarrier modulation and OFDM
- •10.2.1 Multicarrier DS CDMA
- •10.2.2 Conventional MC transmission and OFDM
- •10.2.3 Multicarrier CDMA
- •10.2.4 Applications
- •10.3 Transmit diversity and space–time coding in CDMA systems
- •10.3.1 Transmit diversity and the space–time coding problem
- •10.3.2 Efficiency of transmit diversity
- •10.3.3 Time-switched space–time code
- •10.3.4 Alamouti space–time code
- •10.3.5 Transmit diversity in spread spectrum applications
- •Problems
- •Matlab-based problems
- •11 Examples of operational wireless spread spectrum systems
- •11.1 Preliminary remarks
- •11.2 Global positioning system
- •11.2.1 General system principles and architecture
- •11.2.2 GPS ranging signals
- •11.2.3 Signal processing
- •11.2.4 Accuracy
- •11.2.5 GLONASS and GNSS
- •11.2.6 Applications
- •11.3 Air interfaces cdmaOne (IS-95) and cdma2000
- •11.3.1 Introductory remarks
- •11.3.2 Spreading codes of IS-95
- •11.3.3 Forward link channels of IS-95
- •11.3.3.1 Pilot channel
- •11.3.3.2 Synchronization channel
- •11.3.3.3 Paging channels
- •11.3.3.4 Traffic channels
- •11.3.3.5 Forward link modulation
- •11.3.3.6 MS processing of forward link signal
- •11.3.4 Reverse link of IS-95
- •11.3.4.1 Reverse link traffic channel
- •11.3.4.2 Access channel
- •11.3.4.3 Reverse link modulation
- •11.3.5 Evolution of air interface cdmaOne to cdma2000
- •11.4 Air interface UMTS
- •11.4.1 Preliminaries
- •11.4.2 Types of UMTS channels
- •11.4.3 Dedicated physical uplink channels
- •11.4.4 Common physical uplink channels
- •11.4.5 Uplink channelization codes
- •11.4.6 Uplink scrambling
- •11.4.7 Mapping downlink transport channels to physical channels
- •11.4.8 Downlink physical channels format
- •11.4.9 Downlink channelization codes
- •11.4.10 Downlink scrambling codes
- •11.4.11 Synchronization channel
- •11.4.11.1 General structure
- •11.4.11.2 Primary synchronization code
- •11.4.11.3 Secondary synchronization code
- •References
- •Index
194 |
Spread Spectrum and CDMA |
|
|
than of radar systems, where the terminology stems from. For instance, a great number of regular algorithms for constructing Costas arrays [54], i.e. square (M ¼ N) sonar arrays or FSK sequences having equal length and number of frequencies, are known.
Problems
6.1. The frequency of a rectangular pulse drops linearly throughout its duration T ¼ 10 ms from 110 to 90 MHz. Calculate the processing gain of the signal. What is the approximate duration of the signal at the matched filter output? Sketch the ambiguity function and ambiguity diagram.
6.2.The frequency of a rectangular pulse drops linearly over the first half of its
duration T ¼ 10 ms from 110 to 90 MHz and then grows linearly from 90 to 110 MHz over the second half. Calculate the processing gain of the signal. Sketch the ambiguity function and its low-level and high-level horizontal sections.
6.3.Calculate aperiodic and periodic ACF for a binary Barker code of length N ¼ 11. Try to do it the most economical way.
6.4.Take a periodic sequence faig of period N and form a new sequence fbig picking each dth element of faig: bi ¼ adi, where multiplication in the index is modulo N. Such a transform is called the decimation of faig with index d. Prove that if faig has perfect periodic ACF and d is co-prime to N, fbig also has perfect periodic ACF.
6.5.The binary f 1g code of length N ¼ 5 has periodic ACF Rp(m) ¼ 1, m 6¼0 mod5. Values of its aperiodic ACF are Ra(1) ¼ 0, Ra(2) ¼ 1. Find Ra(3) and Ra(4).
6.6. The binary f 1g code of length N ¼ 5 has constant component a~0 ¼ þ3 and Ra(4) ¼ 1. Find Rp(m) and the rest of the values of Ra(m).
6.7.Can a binary f 1g code of an odd length N > 5 have Ra(5) ¼ 1? Can a binary code of an even length N > 6 have Ra(6) ¼ 1? For an arbitrary binary code formulate and prove the relation between parities of the three values: length N, shift m and level of Ra(m).
6.8.Is it possible for a binary f 1g sequence that Ra(m) ¼ 1, Ra(m þ 1) ¼ 3 for some m? What about parities of Ra(m) and Ra(m þ 1)?
6.9.Is it possible for a binary f 1g sequence that Ra(2) ¼ 2, Rp(2) ¼ 1?
6.10.Suppose someone has found that each of the PSK sequences of length N ¼ 100 at his disposal has non-normalized periodic ACF taking on values 12 at some shifts
m 2 f1, 2, . . . , N 1g. Can a code with a, max < 0:05 be present among them?
6.11. Construct |
a |
matched |
filter |
for |
a |
BPSK |
signal |
manipulated |
by |
a |
sequence |
fþ þþg and show waveforms at its characteristic points, when the filter is |
|||||||||||
input by aperiodic and periodic versions of the signal. |
|
|
|
||||||||
6.12. Construct |
a |
matched |
filter |
for |
a |
BPSK |
signal |
manipulated |
by |
a |
sequence |
fþ þ þ g and show waveforms at its characteristic points when aperiodic and periodic versions of the signal are applied to its input.
6.13. A student has calculated periodic ACF of the binary f 1g sequence of length
N ¼ 21 and |
obtained the following |
values: |
Rp(m1) ¼ 9, Rp(m2) ¼ 3, |
Rp(m4) ¼ 5, |
Rp(m5) ¼ 7, Rp(m6) ¼ 7. |
Can all |
of these results be correct? |
Which (if any) are definitely incorrect? |
|
|
|
Time measurement, synchronization and time-resolution |
195 |
|
|
6.14.Prove the non-existence of minimax binary sequences (Rp(m) ¼ 1, m ¼ 1, 2, . . . , N 1) for lengths N ¼ 17, 21, 29, 33, 37, 45. (Hint: use the same technique as in deriving the necessary conditions for perfect ACF of binary sequences.)
6.15.Prove that decimation of a minimax binary sequence again produces a minimax binary sequence whenever the decimation index is co-prime to the period N.
6.16.Prove that decimation of any periodic sequence does not change the maximal periodic sidelobe, whenever the decimation index is co-prime to the period N.
6.17.Calculate (3 þ 7) 5(6 7 þ 4) þ 1 in GF(11).
6.18.Solve the equation 6x þ 7(5 þ 4 2) 1 ¼ 1 in GF(11).
6.19.Prove that GF(4) cannot be built on the basis of modulo 4 operations.
6.20.Is the sequence of length L ¼ 7 f0100110g a binary m-sequence? What is the
answer if all zeros are replaced by ones and vice versa?
6.21. Construct a binary m-sequence of length L ¼ 15 with an initial loading d0 ¼ 1, d1 ¼ d2 ¼ d3 ¼ 0, draw the structure of its generator and compile a table exhibiting its state changes.
6.22.Prove that in one period of a binary m-sequence of memory n the number of series of successive symbols (01), (10), (11) is 2n 2 while the number of series (00) is smaller by one.
6.23.Someone observes an m-sequence knowing its alphabet and memory but not its coefficients of recurrence (6.13). What is the minimal necessary and sufficient number of observed symbols to recover the coefficients?
6.24.Prove the independence of binary character of a specific choice of primitive element.
6.25.Find a primitive element of GF(13). Build a table of logarithms and binary characters of all non-zero elements of GF(13).
6.26.Build the Legendre sequence of length N ¼ 11, calculate its periodic ACF and compare it with the theoretically predicted one.
6.27.Build the Legendre sequence of length N ¼ 13, calculate its periodic ACF and compare it with the theoretically predicted one.
6.28.Find the cyclic shift of the sequence of Problem 6.26 with minimal aperiodic ACF sidelobe.
6.29.Prove the perfection of periodic ACF for Chu codes of odd lengths.
6.30.Prove the perfection of periodic ACF for Frank codes. (Hint: use representation
i ¼ i1h þ i2, m ¼ m1h þ m2; 0 i1, i2, m1, m2 h 1 and summation over i1, i2 in (5.9).)
6.31.Does an 8-PSK sequence of length N ¼ 64 with perfect periodic ACF exist? If so, construct it.
6.32.Prove the non-existence of QPSK sequences with perfect periodic ACF for odd lengths N.
6.33.Prove the non-existence of QPSK sequence of length N ¼ 30 with perfect periodic ACF.
6.34.Prove that for a ternary f0, 1g sequence with perfect periodic ACF, the number of non-zero elements per period is always a square of an integer.
6.35.Prove the non-existence of ternary f0, 1g sequences having perfect periodic PACF and a single zero per period for any odd length.
6.36.Construct an SLSF, show the effect of sidelobe suppression and find SNR loss for a binary sequence fþ þ þ þ þ g.
196 |
Spread Spectrum and CDMA |
|
|
6.37.Find the SLSF energy loss for a sequence fþ þ þ þ g.
6.38.Find the maximal length FSK sequence with alphabet size M ¼ 4 and no more than one frequency coincidence.
Matlab-based problems
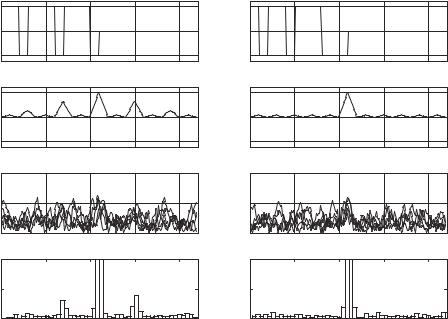
6.39.Using binary codes fþ þ þ þ þ þ þ þ g and fþ þ þ þ þ þ g demonstrate the destructive role of high sidelobes of ACF in time delay measurement and synchronization (Figure 6.24). Recommended steps:
(a)Form the codes given above and oversample them 10 times to simulate baseband signals (complex envelopes) with a rectangular chip.
(b)Plot the signals in two separate subplots.
(c)Calculate the ACFs of the signals above and plot them in two separate subplots.
(d)Extend the signals by appending 110 initial and 110 tail zeros to imitate the stationary regime of a receiver.
(e)Form the observation vector for each signal, adding to it complex Gaussian noise having standard deviations of real and imaginary components three times higher than the signal amplitude.
(f)Calculate the real envelope at the matched filter output for each of the two signals and fix the time moment of its maximum.
|
1 |
|
|
|
|
|
(τ) |
0 |
|
|
|
|
|
S |
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
1 |
|
|
|
|
|
(τ) |
0 |
|
|
|
|
|
R |
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
output |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
MF |
0 |
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
|
100 |
|
|
|
|
|
|
50 |
|
|
|
|
|
|
0 |
0 |
5 |
10 |
15 |
20 |
|
|
|||||
|
|
|
|
t/∆ |
|
|
|
1 |
|
|
|
|
|
(τ) |
0 |
|
|
|
|
|
S |
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
1 |
|
|
|
|
|
(τ) |
0 |
|
|
|
|
|
R |
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
output |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
MF |
0 |
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
|
100 |
|
|
|
|
|
|
50 |
|
|
|
|
|
|
0 |
0 |
5 |
10 |
15 |
20 |
|
|
|||||
|
|
|
|
t/∆ |
|
|
Figure 6.24 ACF sidelobes and time-delay measurement accuracy

Time measurement, synchronization and time-resolution |
197 |
|
|
(g)Do item (e) several times and plot the superposition of waveforms for the two signals separately.
(h)Repeat items (e) (g) 1000 times, display histograms of time estimations for the two signals and interpret the differences between them.
6.40.Using binary codes fþ þ þ þ þ þ þg and fþ þ þ þ þ þ g demonstrate the destructive role of high sidelobes of ACF in time resolution of signals with different intensities (Figure 6.25). Recommended steps:
(a)Form a plain bandpass chip with 10–15 periods of carrier frequency per chip duration and find its ACF.
(b)Find the ACF of the code vectors.
(c)Find and plot matched filter responses to ‘pure’ signals for the two codes.
(d)Display the delayed and attenuated copies of the matched filter responses.
(e)For each of the two signals display the full matched filter responses to the superposition of direct and delayed signals.
(f)Varying the delay and attenuation, compare the masking effect of the sidelobes of the stronger signal on the visibility of the weaker one for the two codes; explain the results.
|
1.0 |
|
|
0.5 |
|
(t) |
0.0 |
|
S |
||
|
||
|
–0.5 |
|
|
–1.0 |
|
|
0 |
|
|
1.0 |
|
τ) |
0.5 |
|
|
||
(t– |
0.0 |
|
S |
||
|
||
|
|
|
a |
–0.5 |
|
|
||
|
–1.0 |
|
|
0 |
|
|
1.0 |
|
|
0.5 |
|
(t) |
0.0 |
|
y |
||
|
||
|
–0.5 |
–1.0
0
5 |
10 |
15 |
20 |
25 |
5 |
10 |
15 |
20 |
25 |
|
|
t/delta |
|
|
5 |
10 |
t/∆ 15 |
20 |
25 |
|
1.0 |
|
|
0.5 |
|
(t) |
0.0 |
|
S |
||
|
||
|
–0.5 |
|
|
–1.0 |
|
|
0 |
|
|
1.0 |
|
τ) |
0.5 |
|
|
||
(t– |
0.0 |
|
S |
||
|
||
|
|
|
a |
–0.5 |
|
|
||
|
–1.0 |
|
|
0 |
|
|
1.0 |
|
|
0.5 |
|
(t) |
0.0 |
|
y |
||
|
||
|
–0.5 |
–1.0
0
5 |
10 |
15 |
20 |
25 |
5 |
10 |
15 |
20 |
25 |
5 |
10 |
15 |
20 |
25 |
|
|
t/∆ |
|
|
Figure 6.25 ACF sidelobes and signal time resolution
6.41. Write a program demonstrating the behaviour of the ACF and spectrum of an LFM pulse with changing deviation. Take three values of deviation (e.g. Wd T ¼ 10, 25, 40). Compare the exact form of the ACF with the approximation
198 |
Spread Spectrum and CDMA |
|
|
(6.1). Run the program for rectangular and bell-shaped pulses and explain the results.
6.42.Write a program calculating and plotting the ambiguity function and its horizontal sections (ambiguity diagrams) at different levels for the LFM (see Figure 6.6) and V-LFM rectangular pulses, whose complex envelopes are:
|
|
S_ t |
|
|
8 exp j |
Td t |
; |
jtj T=2 |
|||||||||||
|
|
|
ð Þ ¼ |
> |
|
|
|
|
W |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
0; jtj > T=2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 exp |
|
j2 |
T |
|
|
; 2 |
|
t < 0 |
|||||||
|
|
|
|
> |
|
|
|
|
|
Wd t2 |
|
T |
|
|
|
||||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
> |
|
|
|
|
|
|
2 |
|
|
|
|
|
T |
||
S t |
|
¼ |
> |
|
|
|
|
|
Wd t |
|
|
|
|
|
|||||
|
|
|
> |
|
|
|
|
j2 |
|
|
|
; |
0 |
|
t |
|
|
|
|
|
ð Þ |
|
> exp |
|
|
|
|
|
|
|
|
||||||||
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
> |
|
|
|
|
|
|
T |
|
|
|
|
|
2 |
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
> |
0; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
> |
t > T=2: |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
> |
|
j |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>
>
>
:
Take three values of deviation (e.g. Wd T ¼ 10, 25, 40), comparing for each of them ambiguity functions and diagrams on high and low levels for both signals.
6.43. Write a program to calculate and plot aperiodic and periodic autocorrelation functions of an arbitrary APSK sequence. Use it to verify the optimality of binary Barker codes. Calculate the ACF of the ternary sequence fþ þ þ þ þ þ0 þ 0 þ þ 0 0 þ 0 g and find the maximal level of its sidelobe relative to the mainlobe. Verify that for binary codes the following properties of periodic ACF are true:
N 1
X
RpðmÞ RpðlÞ ¼ 0 mod4; 8m; l; RpðmÞ ¼ ðNþ N Þ2
m¼0
6.44.Write a program for an exhaustive search for the optimal binary code of given length, minimizing the maximum level of the aperiodic ACF sidelobe. Provide for measuring execution time and try to optimize the processing speed of the program. How does operating time grow when length is incremented by one? What is the maximal length you have managed to find an optimal code for?
6.45.Using Matlab, illustrate time-resolution of three copies of the bandpass periodic APSK signal manipulated with the ternary code ( þ þ þ þ þ þ 0 þ 0 þþ0 0 þ 0 ) at the matched filter output (Figure 6.26). Take time shifts between consecutive copies of 2–3 and 5.5–6.5 chip durations D correspondingly. Recommended steps are:
(a)Form several (3–4) periods of ternary code and oversample them 100 times to simulate rectangular baseband chips manipulated by the given code: the signal complex envelope.

Time measurement, synchronization and time-resolution |
199 |
|
|
(b)Form the sum of three overlapped delayed copies of the complex envelope having remarkably different amplitudes, say in the proportions 1 : 4 : 8.
(c)When summing copies, be mindful of the proper (consistent with delay) phase of a copy, specifying the carrier frequency to be 5/D.
(d)Calculate and plot the resulting bandpass signal at the matched filter input.
(e)Filter the resulting complex envelope with a filter matched to one period of the signal.
(f)Calculate and plot the bandpass filter output.
(g)Run the program for other values of delays and amplitudes, and comment on the results.
|
1 |
|
|
|
|
|
|
|
Signal |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
1st delayed signal
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
input |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
MF |
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
output |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
MF |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
|
|
t/∆ |
|
|
|
|
Figure 6.26 Resolution of three replicas of the signals with perfect periodic ACF
6.46.Write a program generating a binary m-sequence specified by a memory n. Generating m-sequences of various lengths, calculate their PACF (after mapping onto the f 1g alphabet) and check experimentally their balance and shift-and-add properties. Check also the series property: each series (run) of l n fixed consecutive bits occurs 2n l times during the period except for the all-zero run, which occurs 2n l 1 times.
6.47.Testing the binary polynomial of degree n in the LFSR generator may answer the question of whether it is primitive. If the LFSR does generate an m-sequence of length N ¼ 2n 1 then the polynomial is primitive. Write a program performing such a test and tabulate all primitive polynomials of degrees from 4 to 12. Is polynomial f (x) ¼ x6 þ x4 þ x2 þ x þ 1 primitive? What sequence is generated by
LFSR with a feedback defined by this polynomial?

200 |
Spread Spectrum and CDMA |
|
|
6.48.Write a program to build a Legendre sequence. First find a primitive element of a prime field GF(p). Then plus ones should be put in the positions whose numbers are even powers of the primitive element in GF(p) and in position number zero (the latter may alternatively be assigned to 1, too), while the rest of the elements should be minus ones. Run the program for lengths N ¼ 11, 23, 31, 43 and those of your own choice, checking in each case the PACF of the sequence obtained.
6.49.Write a program finding the sequence with minimax aperiodic ACF sidelobes among one-period segments of a given sequence with promising periodic ACF. Running this program along with that of Problem 6.48, find the best (in aperiodic
sidelobe level) one-period segments of Legendre sequences having lengths N ¼ 23, 29, 31, 37, 43, 47, 53, 59, 61, 67. Have you found anything better in a, max than the binary Barker code of length N ¼ 13?
6.50.Write a program forming and testing periodic ACF of modified m- and Legendre sequences (if the leftmost element of the latter is 1 take the negative of the sequence, multiplying all its elements by 1). Verify perfection of periodic ACF for the modified sequences. Derive modified sequences from the initial ones by replacing the 1 symbol by:
(a) a real symbol b ¼ 1 p 2
Nþ1
hi
(b) a complex symbol b |
¼ |
exp |
Nþ1 |
|
j arccos N 1 . |
6.51.Write a program verifying the perfection of periodic ACF of Chu and Frank codes.
6.52.Write a program generating ternary sequences of Section 6.11.3 over prime fields and verifying the perfection of their periodic ACF. An example for the case p ¼ 5, n ¼ 3 (N ¼ 31, ¼ 1:24) is given in Figure 6.27.
(a) |
s(t) |
(b) |
(τ) |
|
R |
||
|
1.0
0.5
0.0
–0.5
–1
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
|
|
τ/∆ |
|
|
|
1.0
0.5
0.0
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
|
|
τ/∆ |
|
|
|
Figure 6.27 Rectangular-chip signal modulated by the ternary sequence (a) and its periodic ACF (b)

Time measurement, synchronization and time-resolution |
201 |
|
|
6.53.Write a program finding SLSF and calculating its SNR loss for a given binary sequence. Plot the signal manipulated by this sequence, its periodic ACF and
SLSF response. An example for |
a |
binary |
sequence f þ þ þ |
|||||||||||
þ þ þ þ þ þ þ þ þ þ þ þþg |
of |
length |
N ¼ 27( dB ¼ 0:4 dB) |
is |
||||||||||
given in Figure 6.28. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(a) |
s(t) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
25 |
30 |
35 |
40 |
45 |
50 |
|
|
|
|
|
|
|
|
|
|
t/∆ |
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
τ) |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
R( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
25 |
30 |
35 |
40 |
45 |
50 |
|
|
|
|
|
|
|
|
|
|
τ/∆ |
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
(c) |
(t) |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
Rsl |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
|
25 |
30 |
35 |
40 |
45 |
50 |
|
|
|
|
|
|
|
|
|
|
t/∆ |
|
|
|
|
|
Figure 6.28 Rectangular-chip signal manipulated by a binary sequence (a), its periodic ACF (b) and SLSF response (c)
6.54.Write a program to calculate aperiodic ACF of a radar array. Run the program to verify the properties of the FSK code in Example 6.13.1.
