3

Merits of spread spectrum

3.1 Jamming immunity

The surrounding environment in which a specific system transmits and retrieves information is not perfectly friendly towards it. Along with thermal noise, interferences of varying physical nature may accompany the useful signal at the receiver input. In particular, interference can emerge as a result of the presence of some other system on the air if its operating frequency is close enough to that of the first system. Following the universally adopted terminology, we will call this sort of interference a jammer.

A great variety of jammer types may be encountered in practice and special measures are as a rule necessary to counter their destructive effect. In this section we will show that the spread spectrum is quite a powerful instrument of jammer neutralization. An exhaustive investigation into system behaviour subject to the combined effects of both jammer and thermal noise would require the calculation of integral performance characteristics such as error probability or estimate precision. The concrete results of this challenging work may be found in books (e.g. [5,6]) and mainly in numerous specialized papers (see, for example, the bibliography in [3]). However, our aim is much more modest and directed at getting a general idea of why and how spread spectrum helps in combating a jammer. For this reason we limit ourselves to only the simplest assessments based on the power ratio between the signal and overall interference. Putting it another way, we choose for the analysis here only the plainest, but still very characteristic, type of jammer, which is approximated by the Gaussian random process whose spectrum overlaps with that of the signal. Sometimes such a simplified approach is fully adequate, as it is in the case of BPSK or ASK data transmission, where the error probability depends only on the ratio referred to above, whenever the overall interference may be assumed Gaussian. Other situations (M-ary transmission, parameter measuring) are not that straightforward and the power ratio does not contain all the necessary information on the performance quality, but still remains indicative as a ‘rule of thumb’ to judge the potential advantages of spread spectrum. We consider two basic models of a jammer, starting with a narrowband one.

Spread Spectrum and CDMA: Principles and Applications Valery P. Ipatov

2005 John Wiley & Sons, Ltd

3.1.1 Narrowband jammer

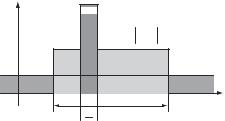
This type of jammer is more typical of situations where some side system or systems have no hostile intentions with respect to the useful system and create a jammer just as a result of normal functioning. Figure 3.1 shows the amplitude spectrum j~s( f ) j of the

~

useful signal and the jammer power spectrum J( f ) approximated by rectangles against the uniform background AWGN power spectrum N0/2. We call a jammer narrowband only to stress that its bandwidth Wj is smaller than the signal bandwidth W and there are areas where the signal spectrum is not corrupted by the jammer. The narrowband jammer may be further classified to partial-band, tone, etc. [3,5,6]; however, for our study the specific value of its bandwidth is immaterial.

First suppose that the useful system undertakes no special measures to combat a jammer except for, maybe, just appropriate signal design. This kind of scenario means that a system designer may foresee the risk of the presence of a jammer and allow for it in the signal choice, but the system is not adaptive, and makes no adjustment of either signal modulation or processing algorithm to the current interference environment. In other words, it uses always only the filter, which is matched to AWGN regardless of the presence or absence of a jammer at the receiver input.

To find the power signal-to-interference ratio (SIR) q2I at the matched filter output note that with a rectangular signal spectrum (where js~( f ) j equals the constant ~s within signal bandwidth W and is zero elsewhere), the filter amplitude transfer function is also uniform within the signal bandwidth W and zero outside it. Without loss of generality we can put its non-zero level equal to 1. Therefore the filter passes a jammer (treated as a random process) to the output without any change of its power J, the filtered AWGN power being N0W. On the other hand, the filter is matched to the signal and sums all signal harmonics coherently to produce the output peak Aout ¼ R11 j~s( f ) j df ¼ 2Ws~, where spectrum uniformity within the bandwidth W is used and doubling is responsible for ‘negative frequencies’. By the same token signal energy calculated through the

Parseval theorem E ¼ R1 j ~s( f ) j2 dt ¼ 2W~s2. Consequently:

1

~

J( f )

~

s( f )

N0 /2

f

W Wj

Figure 3.1 Spectra of signal, jammer and background AWGN

shortening, since otherwise signal energy, SIR and SNR will suffer. Thus, we arrive at the following conclusion: to achieve a higher narrowband jamming immunity with no mobilization of brute-force resource (increase of signal energy or peak power) the only way is to widen the spectrum independently of signal duration, i.e. to use spread spectrum technology.

3.1.2 Barrage jammer

In many military scenarios and intelligence games, a jammer is frequently created deliberately as an electronic countermeasure. In such cases the jammer transmitter may suspect that the system under counteraction will appear smart enough to register the presence of the jammer and properly adapt itself to it. In particular, when the jammer is narrowband the system can resort to band-elimination filtering or even to changing a signal to shift its spectrum to the jammer-free zones. To prevent this, the barrage noise jammer can be engaged whose power spectrum covers the signal spectrum with no gaps (Figure 3.3). It is clear that the barrage jammer corrupts the signal in the same way as an additional AWGN with power spectrum density NJ ¼ J/W. Therefore, the power SNR at the matched filter output of the useful system:

coincides with SIR (3.1). In this case, however, the malignant intent urges the jammer transmitter to provide a much more damaging effect compared to the natural AWGN. It is possible only if J/W N0, resulting in:

We again clearly see that when the peak power of the useful system is limited, and so is the power resource of the jammer transmitter, the involvement of signals with high time–frequency product WT, i.e. spread spectrum ones, is the only instrument at the disposal of the system to improve its immunity towards the barrage jammer.

Formula (3.3) explains another popular name for the time–frequency product WT. As is seen, the ratio between the signal power and the power of a uniform-spectrum noise

N0/2

f

Wj = W

Figure 3.3 Spectra of signal, barrage jammer and background AWGN

within the signal bandwidth increases at the matched filter output 2WT times against the input value P/J. Thus, it is natural to call WT the processing gain.

The conclusions above are well supported visually by two figures, obtained by simulation in Matlab. Figure 3.4 illustrates matched filtering of the plain rectangular signal (column a) and a spread spectrum signal (LFM, WT 50) of the same duration and energy (column b). The same jamming CW interference is added to both signals (second row). While the plain signal is fully masked by the jammer and is not clearly seen at the filter output, the spread spectrum one, time-compressed by the matched filter, is observable distinctively.

In Figure 3.5, where the columns correspond to the same two signals, the upper plots show the signal power spectra. The plots of the second row give the power spectra of two random realizations of different barrage jammers, the same fixed average jammer power being distributed over the signal bandwidth. Because of this the average level of the spectrum in column (b) is about 50 times lower than that in column (a). The third row shows example observed waveforms, where the intensity of the jammer is approximately the same for both signals, which are well hidden under the jammer. As for the lower plots, they again confirm explicitly the superiority of a spread spectrum signal in resistance to a barrage jammer.

In closing, note once again that this section is in no way aimed to answer questions on what sort of jammer is most dangerous in a concrete scenario and what the system should

Figure 3.4 Examples of matched filtered jammer and signal