Spread Spectrum and CDMA

Principles and Applications

Valery P. Ipatov

University of Turku

and

Saint Petersburg Electrotechnical University “LETI”

WILEY

СОДЕРЖАНИЕ

2.6. Обмен между выигрышем от ортогонального кодирования и шириной полосы. 41

2

6.5. Идеальная периодическая АКФ. Бинарные минимаксные последовательности 158

3

4

5

6

1. Широкополосные сигналы и системы

1.1.Основные определения

Внастоящее время термин «spread spectrum» (широкополосный, распределенный спектр) является одним из наиболее употребимых в радиотехническом и телекоммуникационном сообществе. В то же время, оказывается не так просто сформулировать непротиворечивое и точное определение, ясно отделяющее широкополосную философию от «не широкополосной». Конечно, любой эксперт в области проектирования систем или опытный исследователь интуитивно чувствует суть проблемы, однако это не относится ко вновь обратившимся к данной области. Перед ними не ставится задача выработки определения, а только существует потребность дать ответ на стоящую перед ним проблему. С точки зрения цели, которой служит данная книга, представляется полезным посвятить некоторое ее пространство выработке соответствующего объяснения тому, что в дальнейшем тексте понимается под широкополосной концепцией.

Начнем с напоминания основ спектрального анализа. Любой сигнал s(t) конечной

энергии может быть представлен как сумма несчетного числа гармонических колебаний, амплитуды и фазы которых в пределах бесконечно малого диапазона частот [ f , f df ]

Благодаря взаимно однозначному соответствию между представлением сигнала во

~

временной s(t) и частотной s ( f ) области мы вправе произвольно определять то пред-

ставление, которое будет использоваться при решении конкретной задачи. Для характеристики размера зоны, в которой сосредоточена энергия сигнала во временной или частотной области, используются обозначения длительности сигнала T или полосы W соответственно. Сигнал, энергия которого концентрируется в пределах строго ограниченного участка временной оси, не может иметь ограниченный (т.е. ненулевой в конечном частотном интервале) спектр и наоборот. Вследствие этого для определения, по крайней мере, одного из параметров T , W или обоих сразу необходимо принять ряд допущений, касающихся понимания значения длительности и полосы. Этот путь, основанный на понятии эффективного, среднеквадратического и т.п. значения, определяет длительность и полосу как размер зоны, в которой сосредоточена существенная часть энергии сигнала во временной или частотной области [1].

Абсолютно ясно, что тем или иным образом слово «spread» (распределенный, расширенный) указывает на ширину спектра, т.е. большую полосу W сигнала. Однако опять возникает вопрос, что понимать под широким спектром? Что может служить эталоном для сравнения? Для демонстрации того, как определение «широкополосный» вызывает неоднозначное понимание, сошлемся на ряд широко известных книг.

Наиболее часто при объяснении широкополосности встречается положение, утверждающее, что система или сигнал является широкополосными, если занимаемая ими полоса значительно превосходит минимальную полосу, необходимую для передачи информации [1–6]. Наиболее спорным в этом определении является положение о минимальной полосе, необходимой для передачи информации или сообщения. Согласно фундаментальной границе Шеннона спектральная эффективность (т.е. отношение скорости передачи данных R к полосе сигнала W ) системы связи, работающей в условиях гауссовского канала, удовлетворяет неравенству

13

где Eb – энергия сигнала, приходящаяся на один бит информации, N0 – односторонняя

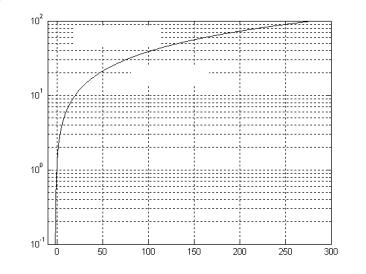
спектральная плотность мощности гауссовского шума. Графическое изображение границы (1.2) представлено на рис.1.1, который показывает, что любые комбинации R /W и

R/W

Запрещ. обл.

Разреш. обл.

Eb/N0

Рис 1.1. Граница Шеннона.

Eb / N0 , лежащие ниже кривой, возможны, по крайней мере, в принципе. Последнее озна-

чает, что теоретический «минимум полосы, необходимой для передачи информации» равен нулю и, следовательно, любая реальная система, которая занимает некоторую ненулевую полосу, может трактоваться как широкополосная. Несомненно, любая попытка использования близкой к нулю полосы для передачи данных потребует значительной энергии сигнала. Так, например, работа со скоростью R 100W требует отношения сигналшум на бит Eb / N0 , равного 280 дБ, что представляется совершенно не реалистичным.

Однако, передача данных в полосе, в десять раз меньшей скорости передачи данных, является типичной для многих цифровых линий связи (радиорелейных линий, модемной связи и т.п.). Данные примеры демонстрируют неопределенность (или бесполезность) использования понятия «минимальной полосы» и доказывают (аргументируют) возможность его использования только в качестве начального пункта при объяснении понятия распределенного спектра, или широкополосности.

В качестве попытки, исключающей указанную двусмысленность, может рассматриваться вариант использования скорости передачи данных, выраженную в битах за секунду, как замену упомянутой выше минимально необходимой полосы [7-8]. Однако, представляется не совсем логичным, что какой-то одной из многих возможных и равноправных единиц измерения скорости передачи данных присваивается особая концептуальная роль. Кроме того, определение широкополосности в терминах ширины полосы, значительно превосходящей скорость передачи данных в битах за секунду, несет определенный риск при охвате систем, которые не относятся к широкополосным. Подтверждением последнего может служить канал связи «вверх» между абонентом и базовой станцией в системе мобильной телефонии GSM. При основной скорости передачи оцифрованной речи в 9,6 кбит/сек абонентский сигнал занимает полосу порядка 200 кГц, что может при-

14

вести к ошибочному решению классифицировать GSM систему, как широкополосную. Однако расширение полосы обратного канала связи GSM системы не связано с особенностями широкополосности. Единственной причиной значительного превышения ширины полосы над скоростью передачи данных является использование метода множественного доступа с временным разделением, который обуславливает работу с укороченными излучаемыми символами по сравнению с временным интервалом, отводимым одному биту информации.

Существует еще одна причина для поиска альтернативных определений. Даже если игнорировать обсужденные ранее трудности, привязывание определения широкополосности к скорости передачи данных или полосе, отводимой для передачи сообщений, может быть оправдано только для систем передачи данных. Однако широкополосная философия находит значительное применение во многих других приложениях, таких как радиолокация, гидролокация, навигация (иначе удаленный контроль за измерением времени и расстояния), разрешения сигналов и пр. Фактически эти системы находились в первых рядах комплексов, реализовавших преимущества, предоставляемые обсуждаемой технологией. В этих приложениях использование таких категорий, как «информационная скорость» или «полоса для передачи данных», представляется затруднительным или, по крайней мере, никак не связанным со стремлением к использованию широкополосности. С целью придания идеям широкополосности универсальности, т.е. возможности применения не только к связным задачам, но и в других областях приложений, следующее определение распределенности спектра (или широкополосности) представляется наиболее уместным.

Обратимся первоначально к принципу неопределенности Габора, согласно которому произведение длительности сигнала на занимаемую им полосу (частотно-временное произведение – time-frequency product) удовлетворяет неравенству WT a , в котором константа a зависит от способа определения длительности и ширины полосы, однако в большинстве случаев ее значение равно единице. Сигнал, для которого WT 1 и, значит, длительность и полоса которого тесно связаны с друг другом, может быть назван простым – plain (не с распределенным спектром или не широкополосным). Единственным способом увеличения полосы, занимаемой простым сигналом, служит уменьшение его длительности, т.е. его укорачивание. С другой стороны, детерминированный сигнал, для которого WT 1 и полоса которого может изменяться независимо от длительности, на-

зывается сигналом с расширенным спектром или широкополосным (spread spectrum).

Другими словами, энергия любого широкополосного сигнала распределена в прямоугольнике на плоскости время–частота, площадь которого значительно больше единицы. Данное определение автоматически определяет также и широкополосную систему: система, основанная на использовании сигналов с распределенным спектром, является широкополосной системой.

Отметим, что в данном определении независимость длительности и полосы выражена явным образом, что означает возможность увеличения ширины полосы (длительности) без уменьшения сигнала во времени (по частоте). Она находит свое отражение в различных способах модуляции (по углу, фазе или частоте) при любых технологиях распределения спектра. Действительно, как амплитудная модуляция может способствовать расширению спектра? Ответ заключается в следующем: только уменьшением зоны, в которой энергия сигнала эффективно распределена во времени, т.е. путем реального уменьшения эффективной длительности сигнала. Таким образом, только угловая модуляция способна расширить спектр сигнала, не оказывая влияния на распределение энергии сигнала во времени.

Иллюстрацией вышесказанному служит рис. 1.2, на котором представлены два прямоугольных импульса одинаковой длительности T с заполнением на несущей частоте f0 : сигнал без внутренней модуляции (а) и сигнал с линейной частотной модуляцией с

девиацией Wd 20 /T (b). Нижние кривые соответственно иллюстрируют вид спектра этих сигналов. Как видно из рисунка, полоса W , занимаемая сигналом, определяется как

15

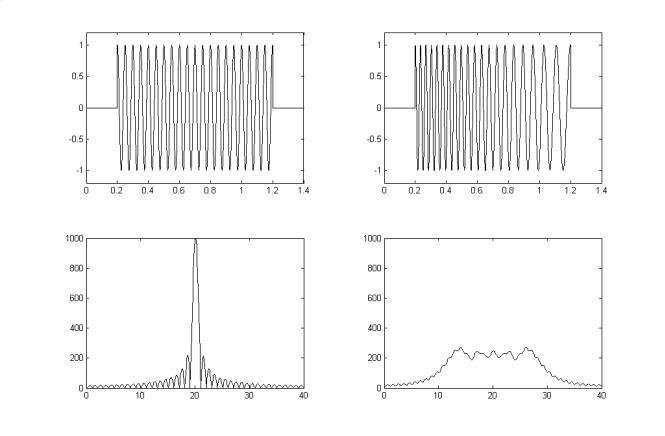
W 1/T , т.е. энергия сигнала распределена в частотной области на интервале, примерно равном обратной величине длительности импульса. Следовательно, длительность и поло-

Рис. 1.2 Немодулированный (a) и частотно–модулированный (b) прямоугольные импульсы и их спектр.

са тесно связаны, а частотно–временное произведение фиксировано и, значит, расширение спектра может быть достигнуто только в обмен на укорочение импульса. В свою очередь полоса, занимаемая импульсом (b), близка к значению девиации (W Wd ) и значительно

больше, чем величина, обратная длительности. В результате независимо от длительности сигнала полоса легко регулируется только изменением девиации. В соответствие с ранее введенным определением первый сигнал относится к простым, а второй – к широкополосным сигналам.

Введенное ранее определение широкополосности фактически является первым, которое широко используется при анализе радиолокационных и родственных им системам, однако оно хорошо согласуется и с задачами, связанными с передачей информации. В связи с чем, в дальнейшем изложении основной упор будет сделан именно на нем.

1.2. Краткий исторический обзор

История технологии распределенного спектра (широкополосности) охватывает шесть десятилетий и может служить предметом собственного изучения. Читатель, заинтересованный в хронологии ключевых событий может обратиться к обширным (однако почти полностью посвященным развитию данного направления в США) обзорам в [9, 10]. Здесь же ограничимся лишь кратким упоминанием основных исторических вех.

Вероятно, что первый патент на РЛС, которую в современной терминологии без сомнения можно отнести к широкополосной, был получен G. Guanella в 1938 г. Далее, в течение Второй Мировой войны и после нее интенсивные исследования в области разра-

16