контрольная (векторная алгебра) 4вариант

a (2;0;1), b (1;1;1), c (1;0; 2)

2, 1, 1

Решение:

1)

а) Найдем векторы b и c:

b 2 (1;1;1) (2;2;2)

c ( 1) (1;0; 2) ( 1;0;2)

Найдем сумму векторов b c:

b c (2;2;2) ( 1;0;2) (2 1;2 0;2 2) (1;2;4)

Найдем скалярное произведение:

a, b c (2;0;1) (1;2;4) 2 1 0 2 1 4 6

b) Найдем векторы a и c:

a 1 (2;0;1) ( 2;0; 1)

c 2 (1;0; 2) (2;0; 4)

Найдем сумму векторов a c:

a c ( 2;0; 1) (2;0; 4) ( 2 2;0 0;( 1) ( 4)) (0;0; 5)

i (1 ( 5) 0 1) j (1 ( 5) 0 1) k (1 0 0 1) 5i 5j 0k

b, a c ( 5;5;0)

1 (0 1 1 1) 0 (2 1 1 1) ( 2) (2 1 1 0) 1 4 5

3) Найдем вектор d a b

d 2 (2;0;1) ( 1) (1;1;1) (4;0;2) (1;1;1) (5;1;3)

Два вектора коллинеарны тогда и только тогда, когда пропорциональны их координаты в некотором базисе.

Задача 2. Даны координаты вершин пирамиды ABCD. Найти:

a.косинус угла между ребрами ABи AD;

b.прAD AC (проекцию вектора AC на вектор AD);

c.SABC (площадь грани ABC)

d.VABCD (объем пирамиды ABCD).

A(1; 1;6), B(4;5; 2), C( 1;3;0), D(6;1;2)

Решение:

а) Косинус вычисляется по следующей формуле:

cos(AB,AD) AB AD AB AD

Найдем векторы AB и AD:

AB (4 1;5 ( 1);( 2) 6) (3;6; 8)

AD (6 1;1 ( 1);2 6) (5;2; 4)

Найдем скалярное произведение векторов AB и AD:

AB,AD 3;6 8 5;2; 4 3 5 6 2 ( 8) ( 4) 59

Найдем модули (длину) векторов AB и AD

AB 32 62 ( 8)2 109

AD 52 22 ( 4)2 45 35

Подставим получившиеся значения в формулу:

b) Найдем проекцию вектора AC на вектор AD по формуле:

прAD AC AD AC AD

Найдем векторы AC и AD:

AC (( 1) 1;3 ( 1);0 6) ( 2;4; 6)

AD (6 1;1 ( 1);2 6) (5;2; 4)

Найдем скалярное произведение векторов AD и AC :

AD,AD (5;2; 4) ( 2;4; 6) 5 ( 2) 2 4 ( 4) ( 6) 22

Найдем модуль (длину) вектора AD :

AD 52 22 ( 4)2 45 35

Подставим получившиеся значения в формулу:

прAD AC 22 3 5

с) Грань ABC пирамиды ABCD является ABC. Площадь ABC находится по формуле:

1

S ABC 2 ABхAC

Найдем векторы AB и AC :

AB (4 1;5 ( 1);( 2) 6) (3;6; 8)

AC (( 1) 1;3 ( 1);0 6) ( 2;4; 6)

Найдем векторное произведение векторов AB и AC :

i (6 ( 6) 4 ( 8)) j (3 ( 6) ( 2) ( 8)) k (3 4 ( 2) 6) 4i 34j 24k

AB,AC ( 4;34;24)

Найдем модуль (длину) AB,AC :

AB,AC ( 4)2 342 242 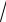1748 2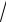437

Подставим получившиеся значения в формулу:

1

S ABC 2 2 437 437

d) Объем пирамиды ABCD находится по формуле:

1

VABCD 6 AB AC AD

Найдем векторы AB, AC и AD:

AB (4 1;5 ( 1);( 2) 6) (3;6; 8)

AC (( 1) 1;3 ( 1);0 6) ( 2;4; 6)

AD (6 1;1 ( 1);2 6) (5;2; 4)

52

8 (( 2) 2 5 4) 48