1

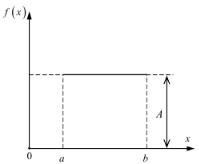
Законы распределения вероятностей случайных величин и результатов измерений.

систематической погрешности, то они принимаются равномерными, так как оцениваются границами (пределами) допускаемых погрешностей.

График равномерного распределения случайной погрешности

называют функцией Лапласа или интегралом вероятности P . Квантили

распределения Лапласа приводятся в справочниках.

Функция F(z) связана( ) =с Ф0,5(z)+соотношениемФ[( − )/ ] = (1 + )/2

Нормальный закон распределения(∆) = 1погрешностей

√2 −(∆−∆ )/(2 2)

Чем больше , тем кривая плотности f(∆) более полога, т.е. увеличивается рассеивание результатов наблюдений.

Графики нормального распределения случайных погрешностей для разных .

обработки результатов измерений.

Центральная предельная теорема утверждает, что закон распределения суммарной погрешности измерений близок к нормальному (усеченному) распределению всякий раз, когда результаты наблюдений формируются под влиянием большого числа независимо действующих случайных составляющих, каждая из которых оказывает лишь незначительное действие по сравнению с суммарной погрешностью. Кроме того, нормальный закон позволяет вести расчеты даже тогда, когда действительный закон неизвестен, потому что нормальный закон дает чаще увеличенный, чем

нормированное нормальное распределение с нулевым средним и единичной дисперсией N(0,1); k = n -1 – число степеней свободы (число независимых значений

квадратов величин).

Плотность вероятности случайной величины X

2

Кривые плотности распределения 2

Распределение t -Стьюдента. Распределение непрерывной случайной

приближается к нормальному распределению.

3

Кривые плотности распределения t -Стьюдента

Распределение гармонического колебания (закон распределения арксинуса).

Гармоническое колебание постоянной амплитуды Umax и постоянной частоты f можно рассматривать как случайную величину, если начальная фаза есть случайная величина. Рассмотрим аддитивную погрешность, вызванную синусоидальной помехой u(t)=Umaxsin2 ft .

распределяемый по нормальному закону также является нормальным. Функции распределения узаконены стандартом ГОСТ 8.011-72.

4

Класс точности приборов и нормирование погрешностей. Методы поверки

Класс точности СИ – обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых устанавливают в стандартах на отдельные виды СИ.

Класс точности характеризует свойства приборов в отношении точности и уже включает систематическую и случайную погрешности. Однако он не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, поскольку точность измерений зависит еще от метода измерений, взаимодействия СИ с ОИ, условий измерения и т.д. В связи с большим разнообразием, как самих СИ,

государственных приемочных испытаний. Если СИ предназначены для измерения одной и той же физической величины, но в разных диапазонах, или – для измерения разных физических величин (ФВ), то этим СИ могут присваиваться разные классы точности, как по диапазонам, так и по измеряемым ФВ.

Способ выражения погрешностей зависит от характера изменения погрешности по диапазонуизмерения, назначения и условий применения СИ.

1)Если погрешность результатов измерений в данной области измерений принято выражать в единицах измерений ФВ или делениях шкалы, то принимается форма абсолютных погрешностей (меры, магазины номинальных ФВ).

2)Если границы абсолютных погрешностей в пределах диапазона измерений практически постоянны, то принимается форма приведенной погрешности.

3)Если эти границы нельзя считать постоянными, то принимается форма относительной погрешности.

Поэтому ГОСТ 8.401-80 в качестве основных устанавливает три вида классов точности СИ:

- для пределов допускаемой абсолютной погрешности в единицах изме-

ряемой ФВ или делениях шкалы; - для пределов допускаемой относител= ± ьной10погрешности в виде ряда чисел:

мультипликативной составляющи, или в виде таблицы, графика функции при нелинейном изменении границ.

Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами.

При этом, чем дальше буква от начала алфавита, тем больше значение допускаемой абсолютной погрешности (С или М).

1

Класс точности через относительную погрешность СИ назначается двумя

измерений высокой точности, в частности цифровых приборов, многозначных мер сопротивления. Класс точности СИ, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается отношением c/d , которое должно удовлетворять условию c/d >1.

Если x N представляется в единицах измеряемой величины, то класс точности обозначается числом, совпадающим с пределом допускаемой приведенной погрешности.

Поверка средств измерений - совокупность операций, выполняемых в целях подтверждения соответствия средств измерений метрологическим требованиям.

В основу классификации применяемых методов поверки положены следующие признаки, в соответствии с которыми средства измерений могут быть поверены:

-без использования компаратора или прибора сравнения, то есть непосредственным сличением поверяемого СИ с эталонным СИ того же вида;

-сличением поверяемого СИ с эталонным СИ того же вида с помощью компаратора или других средств сравнения;

-прямым измерением поверяемым СИ значения физической величины, воспроизводимой эталонной мерой;

-прямым измерением эталонным СИ значения физической величины, воспроизводимой подвергаемой поверке мерой;

-косвенным измерением величины, воспроизводимой мерой или поверяемым прибором, подвергаемыми поверке;

-путем независимой (автономной) поверки.

При поверке методом непосредственного сличения устанавливают требуемые значения измеряемой величины X и сравнивают показания поверяемого прибора Хп и эталонного прибора Хэ. Разность между их показаниями будет определять абсолютную погрешность поверяемого прибора, которую приводят к нормированному значению для получения приведенной погрешности. Основным достоинством метода непосредственного сличения является простота и отсутствие необходимости применения сложного оборудования.

2

Метод сличения при помощи компаратора (прибора сравнения) применяют тогда, когда невозможно или сложно сравнить показания двух приборов или двух мер. Измерения в этом случае выполняют путем введения в схему поверки компаратора, позволяющего косвенно сравнивать две однородные или разнородные физические величины. Компаратором может быть средство измерений, одинаково реагирующее на сигнал эталонного и поверяемого средства измерений.

Метод прямых измерений заключается в прямом измерении поверяемым прибором значения физической величины воспроизводимой мерой. Практическая реализация метода прямых измерений предъявляет к мерам следующие требования:

-возможность воспроизведения мерой той же физической величины, в единицах которой проградуировано поверяемое средство измерений;

-достаточный для перекрытия всего диапазона измерения поверяемого средства измерений диапазон физических величин воспроизводимых мерой;

-соответствие точности меры, а в ряде случаев и ее типа и плавности изменения размера требованиям, которые предъявляются в нормативных документах (НД) по поверке данного средства измерений.

Суть метода косвенных измерений заключается в следующем: проводят прямые измерения нескольких физических величин с помощью эталонных СИ и получают

значения X01 , X02 ,… , X0m. Затем, используя известную функциональную зависимость f между этими величинами и величиной, которая измеряется поверяемым прибором, определяют действительное значения величины, то есть находят результат косвенного измерения по формуле:

Q0 = f(X01 , X02 ,… , X0m)

Метод используется тогда, когда действительные значения величин, измеряемые поверяемым средством измерений невозможно или трудно определить прямым измерением или когда косвенные измерения более простые или точные.

При выполнении поверки методом косвенных измерений следует учитывать тот факт, что конечный результат и по грешность косвенного измерения зависит от составляющих погрешностей прямых измерений. Автономная поверка это поверка без применения эталонных средств измерений (СИ). Она применяется при разработке особо точных СИ, которые невозможно или очень сложно поверить одним из рассмотренных выше методов поверки ввиду отсутствия еще более точных СИ с соответствующими пределами измерении. Суть этой поверки, которая наиболее часто используется для поверки приборов сравнения, заключается в сравнении величин, воспроизводимых отдельными элементами поверяемого СИ с величиной, выбранной в качестве опорной и конструктивно воспроизводимой в самом поверяемом СИ. Например, при поверке m-ной декады потенциометра необходимо убедиться в равенстве падений напряжений на каждой n-ной ступени этой декады. Для этого, выбрав в качестве опорной величины сопротивление первой ступени декады, можно поочередно сравнивать с помощью компаратора падение напряжения на каждой n-ной ступени с падением напряжения на этом сопротивлении. Метод трудоемок, но обладает высокой точностью.

При комплектной поверке средство измерений поверяют в полном комплекте его составных частей, без нарушения взаимосвязей между ними. Погрешности, которые при этом определяют, рассматривают как погрешности, свойственные поверяемому средству измерений как единому целому. При этом средство измерений находится в условиях, максимально приближенных к реальным условиям эксплуатации, что позволяет в ходе поверки выявить многие, присущие поверяемому средству измерений недостатки: дефекты внутреннего монтажа, неисправности переключающих устройств и т.п. С учетом простоты и хорошей достоверности результатов, комплектной поверке всегда, когда это возможно отдают предпочтение.

3

Обработка результатов однократных измерений.

Прямые измерения – это измерения, в результате которых находят непосредственно

Погрешность результата однократного измерения оцениваются на основании априорной

3. Если известны пределы других, не исключенных систематических погрешностей, то при оценке их границ в соответствии с ГОСТ 8.207 – 76 данная погрешность± рассматривается как СВ, распределение равномерно и симметрично в

пределах . Тогда суммарная погрешность определяется по формуле:

= 2

=1

где k – коэффициент, определяемый принятой доверительной вероятностью P (при доверительной вероятности равной 0,95 k = 1,1),

θi – границы i-й неисключенной составляющей погрешности.

Если число m неисключенной СП больше 4, то k выбирают из ряда:

распределенных по нормальному закону, СКО и доверительные границы случайной составляющей суммарной погрешности результата однократного измерения, то

суммарное значение находится:

∑ = 2 ∆= ± =1 ∑

где z – коэффициент нормального распределения соответствующей заданной доверительной вероятности, берется из таблиц Лапласа.

1

5. Если распределения погрешности отличны от нормальных, то оп ределяют их композицию и коэффициент z для заданной доверительной вероятности, а суммарная погрешность результата однократного измерения при известных оценках систематической случайной составляющей рекомендуется оценивать по ГОСТ 8.207 –

76.

6. Если погрешность при однократном наблюдении оказывается выше допустимой, то выбирают более точные СИ или применяют прямые измерения с многократными наблюдениями.

2

Обработка результатов косвенных измерений (Обработка результатов многократных измерений)

Результаты многократных наблюдений, полученных при прямых измерениях величины А называются равноточными (равнорассеянными), если они являются независимыми и одинаково распределенными случайными величинами. Сами измерения проводятся одним наблюдателем в одинаковых условиях внешней среды с помощью одного и того же СИ.

Статистическая обработка группы результатов наблюдения при равноточных измерениях в нормальном распределении этих результатов выполняется в такой же последовательности, как рекомендует ГОСТ 8.207 – 76 и включает следующие этапы:

1) исключаются известные СП из результатов измерения;

2) вычисляются средние арифметические исправленных результатов наблюдения, принимаемых за результат измерения.

3) Вычисляется случайное отклонение υi результата отдельных наблюдений от среднего арифметического исправленных результатов (как по числовому значению, так и по знаку);

4) Вычисляется оценка СКО результата наблюдения; 5) Проверяется гипотеза о том, что результат наблюдения принадлежит

нормальному распределению; 6) Вычисляется оценка СКО результата измерения, доверительные границы

случайной погрешности ε, неисключенных остатков СП θ и погрешности результатов

среднего арифметического значения и определяется совокупностью условий измерения

1