1

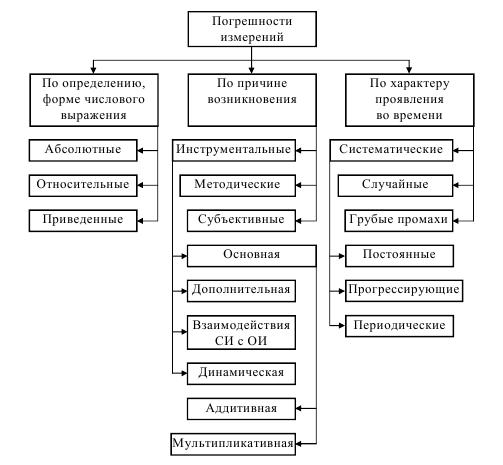
Классификация погрешностей средств измерений.

Измерение как процесс имеет цель сузить интервал неопределенности измеряемой величины. Практика измерений показывает, что как бы тщательно мы ни проводили измерения, какие бы точные средства измерений ни применяли, какими бы совершенными методами и приемами измерения ни пользовались, мы никогда не можем сузить интервал неопределенности до нуля, т.е. узнать истинное значение измеряемой величины.

Мы вынуждены считаться с тем, что результат измерения отражает истинное значение измеряемой величины с некоторой погрешностью. Под погрешностью измерения всегда понимается отклонение результата измерения от истинного значения измеряемой величины.

Термин «точность измерений» не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки используется понятие «погрешности измерений» (чем меньше погрешность, тем выше точность).

Оценка погрешности измерений – одно из важных мероприятий по обеспечению единства измерений.

Погрешности измерений обуславливаются многими характеристиками измерительного процесса. Они зависят от свойств используемых средств измерений, совершенства метода измерений, внешних условий, особенностей канала связи, соединяющего объект измерения и средства измерений, свойств объекта измерений и измеряемой величины, а также субъективных особенностей оператора, фиксирующего показания и т.д.

Погрешности принято классифицировать по трем основным признакам: по определению или форме числового выражения, по причине возникновения и по характеру проявления.

1

I. По определению:

1.Абсолютная;

2.Относительная;

3.Приведенная.

Абсолютная погрешность – это разность между результатом измерения и

возникновения:

1.Инструментальная;

2.Методическая;

3.Субъективная.

Инструментальная погрешность – составляющая погрешности измерений, обусловленная свойствами применяемых СИ (несовершенство конструкции, неточность градуировки, износ, старение и т.д.). Эта погрешность является важнейшей метрологической характеристикой СИ и определяет, насколько действительные свойства СИ близки к номинальным.

Методическая погрешность – составляющая погрешности измерений, обусловленная несовершенством метода измерения, приемами использования СИ, некорректностью расчетных формул и округления результатов.

Субъективная (отсчетная) погрешность – составляющая погрешности измерений,

обусловленная индивидуальными особенностями оператора.

Согласно ГОСТ 8.009 – 84, следует различать четыре составляющие инструментальной погрешности (СИ):

1.1.Основную;

1.2.Дополнительную;

1.3.Взаимодействия СИ и ОИ;

1.4.Динамическую.

Основная погрешность обусловлена неидеальностью собственных свойств СИ и показывает отличие действительной функции преобразования СИ в нормальных условиях от номинальной функции преобразования.

Дополнительная погрешность обусловлена реакцией СИ на изменения внешних влияющих величин, отличных от нормальных и неинформативных параметров входного сигнала.

Неинформативным параметром входного сигнала называется параметр, не используемый для передачи значения измеряемой величины.

Нормальными условиями эксплуатации СИ считаются:

•частота питающей сети – 50 ± 0,5 Гц .

Погрешность взаимодействия СИ и ОИ обусловлена подключением СИ к ОИ и во многих случаях приводит к изменению значения измеряемой величины относительно того значения, которое она имела до подключения СИ к ОИ. Эта составляющая зависит от свойств СИ и ОИ.

Динамическая погрешность обусловлена реакцией СИ на скорость (частоту) изменения входного сигнала. Эта погрешность зависит от динамических свойств (инерционности) СИ, частотного спектра входного сигнала, изменений нагрузки и влияющих величин.

III. По характеру проявления во времени:

1.Систематическая;

2.Случайная;

3.Грубая или промах.

погрешности. Особые трудности представляет выделение систематических погрешностей, так как их природу мы можем не знать и даже не подозревать об их существовании. Оставшиеся необнаруженными систематические погрешности опаснее случайных, так как они устойчиво искажают результаты измерений.

3

Систематические погрешности, методы их учета и исключения

Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону. Эти погрешности в некоторых случаях можно определить экспериментально, а, следовательно, полученный результат измерения может быть уточнен путем введения поправки.

Известен ряд способов исключения систематических погрешностей, которые условно можно разделить на четыре основные группы:

-устранение источников погрешностей до начала измерений;

-исключение погрешностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;

-внесение известных поправок в результат измерения (исключение погрешностей вычислением);

-оценка границ систематических погрешностей, если их нельзя исключить.

По характеру проявления систематические погрешности подразделяются на постоянные, прогрессивные и периодические.

Постоянные систематические погрешности - погрешности, которые в течение всего времени измерений сохраняют свое значение.

Прогрессивные погрешности - погрешности, которые в процессе измерений возрастают или убывают.

Периодические погрешности - погрешности, значения которых являются периодической функцией времени или функцией перемещения указателя измерительного прибора. Такие погрешности встречаются в индикаторах часового типа (приборах с круговой шкалой и

В группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.

Инструментальными погрешностями называют погрешности, причина которых заключается в свойствах применяемых средств измерений. Причиной инструментальных погрешностей является также трение в сочленениях подвижных деталей приборов.

Средствам измерений, имеющим шкалу, присущи погрешности, возникающие в неточности нанесенных отметок шкалы (погрешности градуировки). Инструментальные погрешности могут появляться вследствие износа (размер концевой меры длины уменьшается). Величина износа зависит от интенсивности использования.

Правильность показаний ряда средств измерений может зависеть также от положения их подвижных частей по отношению к неподвижным. Окружающая температура, магнитные и электрические поля, атмосферное давление, влажность воздуха относятся к внешним условиям, приводящим к возникновению погрешностей вследствие их изменения. Если значения отдельных факторов выходят за пределы установленных границ, то это может оказаться причиной появления дополнительных погрешностей.

Если между измеряемым явлением или свойством и принципом действия средства измерений нет теоретически доказанной зависимости, то это может стать причиной возникновения погрешностей метода измерения (теоретических погрешностей).

Погрешности метода измерения являются следствием упрощений или допущений,

1

применения эмпирических формул и зависимостей.

Индивидуальные свойства человека, которые обусловлены особенностями его организма или укоренившимися неправильными навыками, приводят к субъективным систематическим погрешностям.

Способы устранения систематических погрешностей.

Устранение источников погрешностей до начала измерения. Этот способ следует считать наиболее рациональным, так как он освобождает от необходимости устранять погрешности в процессе измерения или вычислять результат с учетом поправок. Так, для устранения температурной погрешности необходимо обеспечить требуемую температуру окружающей среды с допускаемыми колебаниями.

Для устранения влияния на точность измерений внешних магнитных и электрических полей используются различные экраны.

Влияние вредных вибраций на точность измерений может быть устранено за счет использования различного рода амортизаторов.

Влияние влажности и давления на точность измерений может быть исключено, если для измерений использовать, например, специальные камеры.

Для исключения систематических погрешностей в процессе измерения существуют различные способы и приемы без использования специальных установок.

Способ введения поправок основан на знании систематической погрешности и закономерности ее изменения. В этом случае в результат измерения, содержащий систематические погрешности, вносят поправки, равные этим погрешностям, но с обратным знаком.

Способ замещения заключается в том, что измеряемый объект заменяют известной мерой, находящейся при этом в тех же условиях, в каких находился он сам. Способ замещения используется при измерении электрических параметров - сопротивления, емкости, индуктивности.

Способ компенсации погрешности по знаку заключается в том, что измерение производят дважды так, чтобы неизвестная по размеру погрешность входила в результаты с противоположными знаками.

Способ противопоставления имеет большое сходство со способом компенсации по знаку. Он заключается в том, что измерения проводят два раза, причем так, чтобы причина, вызывающая погрешность, при первом измерении оказывала противоположное действие на результат второго.

Способ применяется в тех случаях, когда сравнивается измеряемая величина с мерой примерно равного значения.

Критерии для исключения систематических погрешностей.

Наличие переменной составляющей систематической погрешности (погрешности, изменяющейся по какому-либо закону) искажает оценки характеристик случайной погрешности.

Систематическая погрешность может быть выявлена средствами статистического анализа. Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более точных методов и средств. Существует много различных методов обнаружения систематических погрешностей в результатах измерения. Рассмотрим лишь некоторые из них.

Метод последовательных разностей (Критерий Аббе)

Способ используется для обнаружения изменяющейся во времени систематической

∑( +1 − )2

2( − 1)

Если в процессе измерений происходило смешение центра группирования результатов наблюдений, то D(x) даст завышенную оценку дисперсии результатов наблюдения. Это объясняется тем, что на D(x) влияют вариации X. В то же время изменения центра группирования мало влияют на последовательные разности и смещение почти не отражается

= ( )

на значении Q(x). Вследствие этого отношение ( )

является критерием для обнаружения систематических смешений центра группирования

(критерии Аббе).

Критическая область этого критерия определяется< = как Если полученное значение критерия Аббе меньше , то нулевая гипотеза постоянства

центра группирования результатов измерений (X) отвергается, т. е. имеет место систематическая составляющая.

Комбинаторные критерии Эти критерии позволяют установить наличие систематической погрешности в ряду

измерений только в зависимости от порядка появления результатов наблюдений.

Для этого все результаты наблюдений разбиваются на два вида: А - результаты с положительным отклонением от среднего значения; В - с отрицательным отклонением от среднего значения. Затем рассматривается ряд из n последовательных результатов наблюдений, состоящий из n1 результатов А и n2 результатов В (n1 + n2 = n).

Каждый отрезок последовательности результатов наблюдений одного и того же вида называется серией.

За критерий случайности погрешности измерений может быть принято число серий в ряду наблюдений.

Для полученного n и заданной вероятности Р = 1 - существует интервал, накрывающий

определенное число серий = ( ≤ ≤ )

Предположение о случайном характере распределения серий отвергается, т. е.

предполагается< илиналичие> систематической погрешности, если полученное значение числа серий

Исключение систематической погрешности

Рассмотренные выше критерии позволяют сделать вывод о наличии или отсутствии систематической составляющей в результатах измерений. Для определения закономерности изменения систематической составляющей погрешности можно использовать метод наименьших квадратов.

Наиболее наглядным методом выявления систематической погрешности является графический метод. Суть метода сводится к следующему. На график в координатах Y (результат измерения), X (порядковый номер измерения) наносятся полученные результаты измерений. Для наглядности полученные точки соединяют прямыми линиями. По расположению точек на графике судят о наличии систематической погрешности. Если тенденция в изменении результатов наблюдается, то систематическая погрешность существует и ее следует исключить. В противном случае констатируют, что систематическая погрешность отсутствует (или несущественна).

При использовании МНК параметры определяют из условия: сумма квадратов отклонений фактических значений от рассчитанных по выбранной зависимости была бы минимальной.

3

Случайные погрешности и способы их описания. Промахи измерений.

Случайные погрешности представляют собой погрешности, в появлении каждой из которых не наблюдается какой-либо закономерности. Случайные погрешности неизбежны и неустранимы и всегда присутствуют в результате измерения. Они вызывают рассеяние результатов при многократном и достаточно точном измерении одной и той же величины при неизменных условиях, вызывая различие их в последних значащих цифрах (результаты многократных измерений одной и той же постоянной величины в одних и тех же условиях с помощью одного и того же измерительного устройства одним и тем же оператором могут отличаться друг от друга).

Каждая случайная погрешность возникает в результате воздействия многих факторов, каждый из которых сам по себе не оказывает значительного влияния на результат.

Так как случайные погрешности не поддаются исключению из результатов измерений, то при рассмотрении их влияния на результат измерений задача сводится к изучению свойств совокупностей результатов отдельных наблюдений.

Природа и физическая сущность случайных и систематических составляющих погрешности измерений различна. Однако оценки неисключенных остатков систематических погрешностей и случайных погрешностей осуществляются на основе обработки статистического материала, представляющего собой совокупность результатов измерений.

Для изучения случайных погрешностей используются методы теории вероятностей и математической статистики. Эти методы применимы и для неисключенных систематических составляющих.

Распределения случайных величин

Дискретные и непрерывные случайные величины. По своей физической природе измеряемые величины могут быть детерминированными и случайными.

Дискретной (прерывной) называют случайную величину, отдельные значения которой можно перенумеровать.

Непрерывной называют случайную величину, возможные значения которой непрерывно заполняют некоторый промежуток.

Случайная величина не может характеризоваться каким-то одним значением. Для нее необходимо обязательно указать множество возможных значений и вероятностные характеристики, заданные на этом множестве.

Вероятностным описанием случайной величины является закон ее распределения. Законом распределения случайной величины называют соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может быть задан в различной форме.

Задание функции распределения является обшей формой закона распределения как для дискретных, так и для непрерывных случайных величин. Функцию распределения можно задать в виде интегрального закона распределения (функция распределения) и в виде

вероятности имеет размерность, обратную размерности случайной величины.

1

Законов распределения случайных величин.

Закон нормального распределения находит большое применение в различных отраслях техники. Этому закону подчиняются многие непрерывные случайные величины, встречающиеся в технике, например ошибки измерения, высота микронеровностей обработанной поверхности и многие другие. Широкое применение закона нормального распределения объясняется центральной предельной теоремой. Из этой теоремы следует, что если случайная величина X представляет сумму очень большого числа взаимно независимых случайных величин х1, х2, хn влияние каждой из которых на всю сумму незначительно, то независимо от того, каким законам распределения подчиняются слагаемые х1, х2, хn сама величина X будет иметь распределение вероятностей, близкое к нормальному, и тем точнее, чем больше число слагаемых. Теорема Ляпунова дает теоретическое объяснение и тому факту, что при устойчивом процессе обработки деталей на настроенных станках и при отсутствии изменяющихся во времени систематических погрешностей действительные размеры деталей часто подчиняются закону нормального распределения, так как результирующую погрешность обработки можно представить как сумму большого числа погрешностей, зависящих от станка, приспособления, инструмента и заготовки.

Плотность вероятности или дифференциальная функция распределения случайной вели-

Дифференциальная функция нормального распределения графически выражается в виде кривой колоколообразного типа. Из вида кривой нормального распределения следует, что

с одинаковой вероятностью может принимать любое значение в заданных пределах.

Числовые характеристики случайных величин

Для изучения распределения случайных величин пользуются рядом числовых характеристик: мер положении и мер рассеивания.

К характеристикам положения относятся: математическое ожидание, мода, медиана. Математическое ожидание случайной величины называют также средним значением случайной величины.

Модой называют значение случайной величины, имеющее у дискретной величины наибольшую вероятность, а у непрерывной - наибольшую плотность вероятности. Если кривая распределения имеет один максимум, то мода равна значению случайной величины, соответствующей этому максимуму. Такая кривая называется унимодальной (одномодальной). Если кривая распределения имеет два или несколько случайной величины одинаковых максимумов, то она соответственно называется двухмодульной, или многомодальной.

Медианой случайной величины называют такое ее значение, для которого функция распределения равна 0,5. Это означает, что вероятность случайной величины принять значение меньше медианы в точности равна вероятности этой величины принять значение, большее медианы.

2

Геометрически медиана представляет собой абсциссу точки, которая делит площадь, ограниченную кривой распределения, пополам.

Наряду с характеристиками положения используются числовые характеристики, по которым судят о рассеивании случайной величины. К ним, в частности, относят дисперсию и среднеквадратическое отклонение.

Дисперсией дискретной случайной величины называется сумма квадратов отклонений случайной величины ее математического ожидания, умноженная на соответствующие вероятности.

Среднеквадратическим отклонением случайной величины называют положительное значение квадратного корня из дисперсии.

Моменты случайных величин

Для исследования распределений случайных величин в математической статистике пользуются моментами. Моменты представляют собой систему численных характеристик распределения, включающую среднюю арифметическую и дисперсию.

Моментом ряда распределения (или просто моментом) относительно начального значения

= ( − )′

Обычно для практических целей ограничиваются вычислением моментов не выше четвертого порядка.

Среднее арифметическое значение случайной величины представляет собой начальный момент первого порядка.

Грубые погрешности и промахи

Источниками промахов нередко бывают ошибки, допущенные оператором при измерении. Наиболее характерными из них являются: неправильный отсчет по шкале измерительного устройства, неправильная запись результата наблюдения (описка), неправильная запись значений отдельных мер использованного набора и т. п., ошибки при действиях с приборами, если они повторяются при измерениях.

Причинами грубых погрешностей могут быть внезапные или кратковременные изменения условий измерения или незамеченные неисправности в аппаратуре.

Критерии грубых погрешностей

Известен ряд критериев, которые позволяют исключить грубые промахи. К ним, в частности, можно отнести критерий Греббса (Смирнова), Шарлье, Шовенэ и др. Эти критерии основаны на статистических оценках параметров распределения, так как в

где - результат измерения, вызывающий сомнение; - среднее арифметическое значение

ряда измерений; - среднее квадратичное отклонение результатов измерения. Критическая область значений этого критерия> определяется= как

Если при выбранном уровне значимости q и числе наблюдений n критерий Кr> Zq, то результат отбрасывают как содержащий грубую погрешность.

Порядок обнаружения и исключения грубых погрешностей и промахов с использованием критерия Греббса (Смирнова) сводится к следующему:

-определяется среднее значение результатов измерения

-определяется оценка среднего квадратичного отклонения 5(дг)

-принимается уровень значимости из ряда: 0,001; 0,025; 0,05; 0,1;

-определяется расчетное (критическое) значение критерия Греббса (Смирнова) для принятого уровня значимости q - Zq,n;

-определяется критерий Греббса (Смирнова)

-сравниваются значения Кr и Zq:

если Кr > Zq, то результат отбрасывают как содержащий грубую погрешность;

если Кr < Zq то результат не содержит грубой ошибки с принятой вероятностью Р = 1 - q.

Критерий Шарлье

Критерий Шарлье целесообразно применять лишь для рядов измерений, в котором n > 20. Если число результатов измерения n > 20, то по теореме Бернулли число результатов, превышающих по абсолютному значению Кш , будет равно n[1 - Ф(Кш)], где Ф(Кш) - значение нормированной функции Лапласа для Z = Кш.

Порядок обнаружения и исключения грубых погрешностей и промахов с использованием критерия Шарлье сводится к следующему:

- определяется среднее значение результатов измерения - определяется оценка среднего квадратичного отклонения

Критерий Шовенэ

Критерий Шовенэ основан на тех же предпосылках, что и критерий Шарлье. Его можно использовать, если количество результатов измерения меньше 20.

Критическая область для этого критерияФ( определяется) > 2 − 1 неравенством

ш 2

шРезультаты, значения которых в ряду из n наблюдений превосходят по модулю значение , отбрасываются как промахи. Исключение результатов выполняют в такой

последовательности.

Сначала отбрасывают один результат с наибольшим по модулю отклонением от х и снова подсчитывают . Если и в этом случае критерий Шовенэ нарушается, то исключают следующий с наибольшим отклонением и т. д.

Порядок обнаружения и исключения грубых ошибок и промахов с использованием критерия Шовенэ аналогичен проверке по критерию Шарлье.

4