X͞ гр. I осуществляется по формуле:

х͞ _{ариф. взв.} =

где ƒ - число единиц в каждой группе.

Номер цеха	Средний стаж работы, лет x͞ гр	Число рабочих, чел. ƒ
1-й	5	90
2-й	7	60
3-й	10	50
Итого	_ _	200

В этом примере вариантами являются не индивидуальные данные о стаже работы отдельных рабочих, а средние по каждому цеху x͞ _гр . Весами ƒ являются численности рабочих в цехах. Отсюда средний стаж работы рабочих по всему предприятию составит:

х͞ _ариф = = = 6,85 лет.

Если значение усредняемого признака заданы в виде интервалов. , т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд.

Пример. Распределение рабочих АО по уровню оплаты труда:

Исходные данные			Расчетные значения
Группы рабочих по оплате труда, руб	Число рабочих,чел., ƒ	Середина интервала, руб. х		Х*ƒ
До 10000	5	9000		45000
10000-12000	15	11000		165000
12000-14000	20	13000		260000
14000-16000	30	15000		450000
16000-18000	16	17000		272000
18000 и более	14	19000		266000
Итого	100			1458000

От интервального ряда перейдем к дискретному путем замены интервальных значений их средним значениям (простая средняя арифметическая между верхней и нижней границами каждого интервала). При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и предпоследний).

При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал

После того, как найдены середины интервалов, вычисления делают так же, как и в дискретном ряду, - варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов):

х͞ _ариф = = = 1558 руб

Получили, что средний уровень оплаты труда рабочих АО составляет 14580 руб. в месяц.

Свойства средней арифметической величины.

1. Сумма отклонений индивидуальных значений признака от его среднего значения равно нулю. Доказательство:

- x͞ ) = (x₁ -x͞ ) + (x₂ - x͞ ) +…+(x_n - x͞ ) = x₁ + x₂ +…+ x_n - nx͞ = - n=0

Примечание. Для взвешенной средней сумма взвешенных отклонений равна нулю.

2. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз.

Доказательство:

= = /c=

Вследствие этого свойства индивидуальные значения признака можно сократить в с раз, произвести расчет средней и результат умножить на с.

3. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на это же число.

Доказательство:

= = = x͞ +c

Это свойство полезно использовать при расчете средней величины из многообразных и слабо варьирующих значений признака.

4.Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится.

Доказательство:

= = x͞

Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерения.

5. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа.

Доказательство:

Составим сумму квадратов отклонений от переменной а:

ƒ(a) =

Чтобы найти экстремум этой функции, нужно ее производную по а приравнять нулю:

= 2

Отсюда имеем:

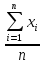n · a= ; a== x͞

Таким образом, экстремум суммы квадратов отклонений достигается при а=х͞. Так как логически ясно, что максимума функции не может иметь, этот экстремум является минимумом.

6. Произведение средней на сумму весов всегда равно сумме произведений вариантов на частоты

x͞ ·

Следствие: исчисляя среднюю, мы уравниваем конкретные варианты, заменяя их одним средним числом, которое как постоянный множитель выносим из-под знака суммы.

Необходимо также отметить, что если все веса равны между собой, то средняя арифметическая взвешенная совпадает со средней арифметической простой.

Средняя гармоническая величина.

Если по условию задачи необходимо, чтобы неизменной оставалась при осреднении сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней.

Средняя гармоническая применяется в тех случаях, когда частоты (веса) не приводятся непосредственно, а входят сомножителями в один из имеющихся показателей.

Средняя гармоническая взвешенная. Данная форма используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Рассмотрим расчет средней урожайности, являющейся одним из основных показателей эффективности сельскохозяйственного производства.