Методы спуска
Ксожалению, за исключением редких случаев, точное решение задачи
одномерной минимизации невозможно, поскольку задача |
|||||
нелинейна( |
. Одна |
f |
|||
|
|||||
x |
k ) |
d |
(k ) |
|
|
из возможных стратегий заключается в аппроксимации |
|||||
функции |
|
вдоль |
|||
прямой |
|
|
|
|
полиномом и минимизации этого |
полинома по
переменной .
Квадратичная интерполяция (вдоль направления спуска) –
метод Пауэлла.
Кубическая интерполяция – метод Давидона.
11В общем случае процесс решения задачи одномерной
минимизации для
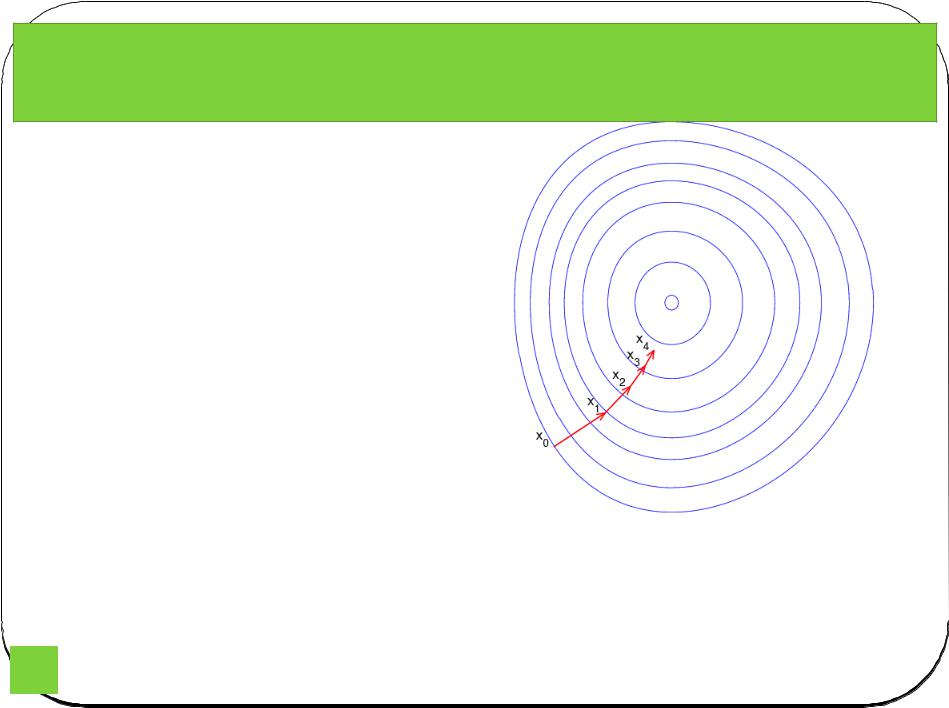
Градиентный спуск
Иллюстрация последовательны х приближений к точке экстремума в направлении наискорейшего спуска (красн.) в случае дробного шага. Синим отмечены
Градиентныйлинииспускуровня— метод нахождения. локального минимума (максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.
Сходимость метода градиентного спуска зависит от отношения максимального и минимального собственных чисел матрицы Гессе в окрестности минимума (максимума). Чем больше это
12 отношение, тем хуже сходимость метода.
Методы спуска
Последовательные приближения градиентного метода для функции
13
Линейный поиск
restart:with(VectorCalculus):with(plots):with(plottools):
z:=(x,y)->sin(1/2*x^2-1/4*y^2+3)*cos(2*x+1-exp(y)):
> grad:=VectorCalculus[Gradient](z(x,y),[x,y]);
> plot3d(z(x,y),x=-1.2..1.2,y=-1.2..1.2,axes=normal,numpoints=1000);p3d:=%:
> contourplot(z(x,y),x=-1.2..1.2,y=-1.2..1.2, axes=normal, contours=30, numpoints=3000);cont:=%:
> start:=[-1/4,1/3];ptf[0]:=Vector(start):
> steps:=15;
> for i from 0 to steps do: print(ptf[i]): pt[i]:=Vector([convert(ptf[i],list)[],z(ptf[i][1],ptf[i] [2])]): dir[i]:=evalf(Normalize(evalVF(grad,ptf[i])));
par[i]:=ptf[i]+lambda*dir[i]; lambd[i]:=fsolve(diff(z(par[i][1],par[i] [2]),lambda)=0,lambda=0); ptf[i+1]:=eval(par[i],lambda=lambd[i]); od:i:='i':
> display(cont,'point(convert(ptf[i],list),color=blue)'$'i'=0..steps,'plot([par[i][1], par[i] [2],lambda=0..lambd[i]])'$'i'=0..steps);
>
display(p3d,'point(convert(pt[i],list),color=blue,symbol=circle,symbolsize=4)'$'i'=0..steps, 'spacecurve([par[i][1],par[i][2],z(par[i][1],par[i][2])],lambda=0
14
Функция Розенброка
Метод градиентного спуска оказывается очень медленным при движении вдоль оврага. Примером такой функции является
функции Розенброка.
In mathematical optimization, the Rosenbrock function is a non-convex function used as a performance test problem for optimization algorithms introduced by Rosenbrock (1960). It is also known as Rosenbrock's valley or Rosenbrock's banana function.
The global minimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial. To converge to the global minimum, however, is difficult.
ItItishasdefineda globalbyminimum at (x,y) = (1,1) where f(x,y) = 0. A different coefficient of the second term is sometimes given, but this does not affect the position of the global minimum. http://demonstrations.wolfram.com/MinimizingTheRosenbrockFunction
/
15
Функция Розенброка
The Rosenbrock function has a narrow curved valley which contains the minimum. The bottom of the valley is very flat. Because of the curved flat valley the optimization is zig- zagging slowly with small stepsizes towards the minimum.
16
Функция Розенброка
17
Функция Химмельблау
In mathematical optimization, the Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:
s one local maximum at |
and |
and four identical local minimums:
The locations of all the minima can be found analytically, but the expressions are long and complicated.
http://en.wikipedia.org/wiki/Himmelblau%27s_function
18
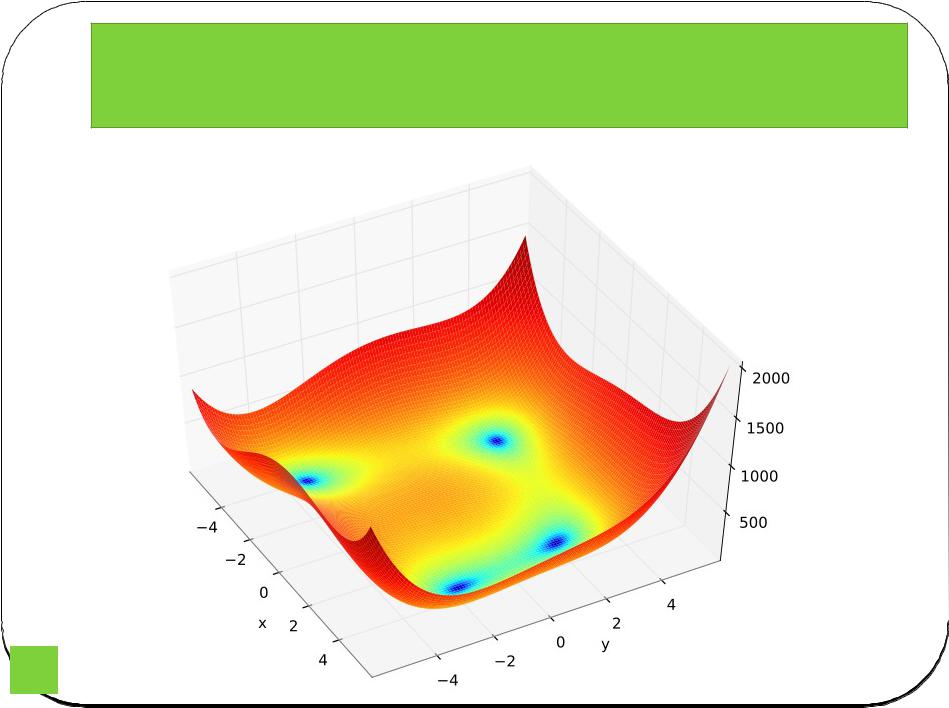
Функция Химмельблау
19
Градиентный спуск
http://en.wikipedia.org/wiki/Gradient_desce nt
20