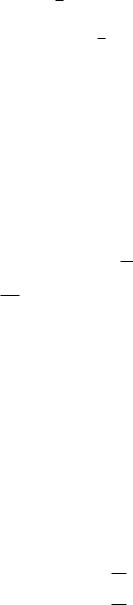6. Двойные, тройные и криволинейные интегралы
6.1.Двойные интегралы
6.1.1.Изменить порядок интегрирования:
n |
y+m |
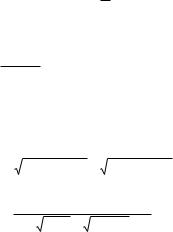
à) ò dy |
ò f (x, y) dx; |
0my/ n
m |
(x / m)2 |
m+n |
(m+n−x)/ n |
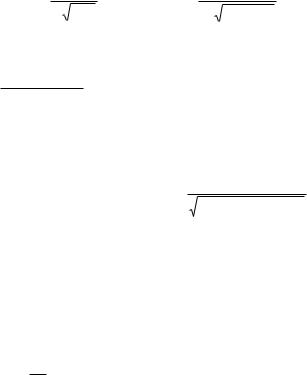
á) ò |
dx |
ò |
f (x,y) dy + ò dx |
ò f (x, y) dy. |
0 |
|
0 |
m |
0 |
6.1.2. Сделать чертеж и найти объем тела, ограниченного по-
верхностями z = 0, y = x2 и плоскостью, проходящей через точки А (n; n2; 0), B (–m; n2; 0) è Ñ (0; 0; m + n).
6.1.3. Сделать чертеж и найти площадь фигуры, ограничен-
ной линиями:
à) y = 0, y = x2, ny = –m2 (x – m – n); á) õ2 + y2 ³ 6, õ2 + y2 £ 2nx + 2ny.
6.2.Тройные интегралы
6.2.1.Найти òòò x dx dy dz, если тело V ограничено плоскостя-
V
ìè x = 0, y = 0, n2x + m2y – mnz = 0 è x + y + z – m – n = 0.
6.2.2. Найти объем тела, ограниченного поверхностями nz = x2 + y2, z = n, x = 0, ny = mx.
6.3.Криволинейные интегралы
6.3.1.Вычислить
ò P (x, y) dx + Q (x, y) dy,
C
где P (x, y) = ny + 2x, Q (x, y) = mx + 2y, а контур С образован линиями n2y = m2x2, y = m2, x = 0:
a) непосредственно; б) по формуле Грина.