шапкин задачи с решениями

Событие является фактом окончания всех предшествующих д анномусобытиюработ,либоначаломработ,следующихнепосре дственно за данным событием. Для совершения события не требуетс я никаких затрат, а само событие не имеет продолжительности.

При составлении сетевого графика необходимо обеспечить логическую последовательность наступления событий, кот орая определяется взаимосвязью и последовательностью выполн ения соответствующих работ. На сетевом графике события обозна ча- ются кружками, в которые в определенной последовательнос ти вписываются цифры.

Приведем следующий простейший график:

1 2 3 4

Из графика следует, что событие 3 не может наступить, пока не совершится событие 2 и т.д. При этом событие 2 называется последующим по отношению к событию 1, так же как событие 4 является последующим по отношению к событию 3. Событие 3 — предшествующее по отношению к событию 4. В указанных определениях имеется в виду, что события следуют одно за други м и между ними нет промежуточных событий. Одно событие может иметь и несколько предшествующих, либо последующих событ ий. Например, на графике (рис. 88) событие 6 имеет два предшествующих события (4 и 5).

Ðèñ. 88

391

Если наступлению данного события не предшествует какаялибо работа, то это событие называется исходным (на рис. 88 эт о событие 1). Событие, не имеющее последующих работ, называет - ся завершающим, т.е. наступлением завершающего события до с- тигается конечная цель данной разработки (на рис. 88 это соб ы- тие 11).

Операция — это сама работа или действие. Она обозначается :

tij

Это означает, что начальное событие i происходит раньше конечного события j, а длительность операции (i – j), которая обозначается стрелкой, будет равна tij.

Фиктивной называется работа, не требующая затрат рабоче- го времени и ресурсов на ее выполнение. Она характеризует зависимость выполнения данной работы от выполнения какой-то д ругой. Длительность этой работы tij = 0 (на рис. 88 это работа 7—9).

Продолжительность выполнения работы измеряется в едини - цах времени: часах, днях, неделях и т.д.

Любая последовательность работ в сети, в которой конечное событие каждой работы последовательности совпадает с на чальным событием следующей за ней работы, называется путем.

Следует различать два вида пути:

1)полным путем называется непрерывная последовательност ь выполнения работ от исходного до завершающего события;

2)критическим путем называется путь от исходного до завер - шающего события, который характеризуется наибольшей про должительностью выполнения работ, находящихся на этом пути.

Первичный сетевой график составляется на основе исходны х (первичных) данных представленных ответственными исполн ителями этапов комплексной работы до его оптимизации.

Рассмотрим детальнее сетевой график некоторого комплек са работ, который необходимо выполнить, чтобы организовать п роизводство нового вида изделия (рис. 88).

В практическом применении сетевых графиков может быть различное количество событий и работ, характеризующих те или иные виды разработок. При этом, если количество событий не

392

превышает 300, графики обсчитывают с помощью простейших микрокалькуляторов. При числе же событий свыше 300, и в особенности 500—1000 и более, параметры сети рассматриваются при помощи ЭВМ.

Определяем продолжительности полных путей, для чего составляем табл. 7.13.

Отсюда видно, что продолжительность критического пути, т. е. пути, имеющего наибольшую продолжительность, равна Têð = 55 (дней). Это означает, что при прочих равных условиях раньше чем через 55 (дней) данная работа не закончится. Следовательно, п родолжительность критического пути представляет собой на иболее ранний срок завершения всей работы от исходного до заверш ающего события.

В сети может быть несколько критических путей.

393

7.2.1.2. Временные параметры сетей. Резервы времени

Основными временными параметрами сетей являются ранние и поздние сроки наступления событий. Зная их, можно вычисл ить остальные параметры сети — сроки начала и окончания работ и резервы времени событий и работ.

Рассмотрим работу (i – j):

[tï(i)] [tï( j)]

Ранний возможный срок < tp (i) > наступления события j есть наименьший возможный срок окончания данной работы:

т.е. раннее возможное событие j равно раннему возможному предшествующему событию i, сложенному с длительностью работы (i – j).

Когда для события j имеется несколько ранних возможных, то берется наибольшее.

Очевидно, максимальное значение раннего окончания работы будет характеризовать продолжительность критическог о пути

(Òêð).

Поздним допустимым сроком наступления события называет - ся максимально допустимый срок наступления этого событи я, не требующий увеличения времени на осуществление всего про екта.

Позднее допустимое равняется разности позднего окончан ия события j и продолжительности последующих работ.

Если для события i будет несколько поздних допустимых, то берется наименьшее.

Работы, у которых < tp ( j) > è [tï (i)] совпадают, называются критическими работами, лежащими на критическом пути. Это есть второй способ определения критического пути.

394

Как уже отмечалось, продолжительность критического пути больше продолжительности любого другого пути сетевого г рафика.

Разность между продолжительностью критического пути Тêð и продолжительностью пути L – T (L) называется резервом времени пути L.

Резерв времени R (L) показывает, на сколько могут в сумме быть увеличены продолжительности работ, принадлежащих п ути L, без влияния на срок проекта.

Различают четыре резерва времени:

Полный резерв времени — это количество времени, на которое можно перенести начало работ или увеличить продолжит ельность без изменения общего срока проекта.

Из этого определения следует, что полный резерв времени п о отдельным работам позволяет маневрировать ресурсами с т ем, чтобы наилучшим образом выполнить всю разработку. Полный резерв времени является зависимым резервом, т.е. его приме нение может привести к изменению резервов по другим работам. По - этому при использовании полного резерва времени обычно п ере- считывают параметры сетевого графика для определения но вого распределения резервов.

Свободный резерв времени — это количество времени, на которое можно перенести начало работ или увеличить их продо л- жительность без изменения раннего начала последующих ра бот, этот резерв может быть использован непосредственно испо лнителем той или иной работы, и это не повлечет за собой изменени я условий производства последующих работ. Полный же резерв времени может быть использован только с разрешения центр а, так как его использование изменяет ранние сроки начала после дующих работ.

Всегда ПР > CP.

На критическом пути все резервы времени равны нулю.

395

Это свойство может служить третьим определением критиче с- кого пути.

Независимый резерв времени означает запас времени, который имеет исполнитель, когда предшествующие работы закан чи- ваются в неудобные для него сроки, а он заканчивает свою ра боту в ранний срок, не расходуя резервов следующих за ним работ .

Гарантированный резерв означает для исполнителя работы резерв времени, который он имеет, когда исполнители предш е- ствующих работ заканчивают их в неудобные для него поздни е допустимые сроки, но и он сдает свою работу в поздний срок.

Åñëè Rc (i; j) è Rí (i; j) имеют отрицательные значения, то эти резервы заменяются нулем.

Существуют различные формы расчета параметров сети: табличный и графический. Наиболее удобной является таблична я форма.

Для рассмотренного примера сетевого графика (рис. 88)

âтабл. 7.14 приведены ранние и поздние сроки окончания и нача - ла работ и резервы времени.

При анализе графика прежде всего обращают внимание на критические работы, от которых в решающей степени зависит своевременное и качественное выполнение всей разработк и. Следует также обращать внимание на наличие резервов времени по отдельным работам. Например, по работе (5, 7) свободный резерв составляет 7 дней. Это означает, что продолжительност ь выполнения данной работы при необходимости можно «растяну ть»

âпределах семи дней, либо начать эту работу позже.

Нахождение величины резервов нельзя рассматривать, одна - ко, как оценку времени простоя исполнителей. На выполнени е работ сетевого графика при правильном планировании выде ляются ресурсы (в человеко-часах, машино-часах и т.д.), равные с уммарной трудоемкости всех предусмотренных работ.

Оценка резервов времени позволяет более рационально рас - пределить трудовые и материальные ресурсы по работам гра фика. Большинство работ обладает закономерностью: увеличив ая число исполнителей, удается уменьшить длительность выпо лнения работы. Эта закономерность может иметь разные формы, н о

чаще других встречается гиперболическая зависимость t = a + xb длительности работы t от количества работников х.

396

Ò à á ë è ö à 7.14

Перебрасывая людей и технику с ненапряженных работ на напряженные работы критического пути, можно сократить ср оки выполнения всего комплекса работ.

Одним из важнейших преимуществ применения сетевых графиков является возможность их оптимизации по различным п ризнакам: по времени (сокращение Тêð), по людским ресурсам, по материальным ресурсам, по стоимости и технико-экономичес ким показателям, а также по различным сочетаниям этих признак ов.

Так, например, оптимизация сетевого графика по времени предполагает, прежде всего, нахождение возможности сокра щения продолжительности критического пути. Это может быть д остигнуто различными путями.

397

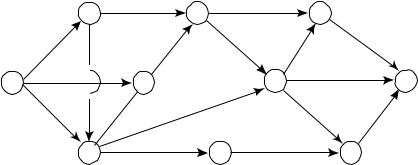
Из сетевого графика видно, что сокращение общей продолжительности выполнения разработки возможно только за счет сокращения продолжительности выполнения работ, лежащих на критическом пути.

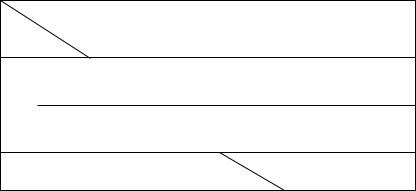
7.2.1.3. Пример построения сетевого графика задачи 15.1 контрольной работы (рис. 89).

Ðèñ. 89

7.2.2.Межотраслевой баланс

7.2.2.1.Модель межотраслевого баланса

Балансовый метод применяется для анализа, нормирования, прогноза и планирования производства и распределения пр одукции на различных уровнях — от отдельного предприятия до н а- родного хозяйства в целом.

Центральная идея межотраслевого баланса (МОБ) заключа- ется в том, что каждая отрасль в нем рассматривается и как п роизводитель, и как потребитель. Модель МОБ — одна из самых простых экономико-математических моделей. Она представл яет собой единую взаимосвязанную систему информации о взаим ных поставках продукции между всеми отраслями производства , а также об объеме и отраслевой структуре основных производственных фондов, обеспеченности народного хозяйства ресурсам и труда и т.д.

Такая модель позволяет рассчитать сбалансированный пла н на основе точного учета всех межотраслевых связей и рассм от-

398

реть при этом множество возможных вариантов. В основе исс ледований балансовых моделей лежат балансовые таблицы, сод ержащие данные о производстве и потреблении продукции различ- ных отраслей или предприятий. Характерные черты и особенн ости этого метода описываются с помощью матричных моделей баланса. Из математических методов здесь главным образом используется аппарат линейной алгебры.

Рассмотрим пример предельно упрощенной системы, состоящей из двух производственных отраслей. Пусть исполнение б а- ланса за предшествующий период характеризуется данными , приведенными в табл. 7.15.

Продукция каждой отрасли частично идет на внешнее потреб - ление (конечный продукт), а частично используется в качест ве сырья, полуфабрикатов или других средств производства в д ругих отраслях, в том числе и в данной. Эту часть продукции на зывают производственным потреблением. Поэтому каждая из ра с- сматриваемых отраслей выступает и как производитель про дукции (1-й столбец продукции) и как ее потребитель (1-я строка таблицы). Приведенную таблицу конкретного примера можно записать и в более общем виде (табл. 7.16).

Обозначим через xi валовый выпуск продукции i-й отрасли за планируемый период и через yi — конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средст ва производства других экономических систем, потребление насе ления, образование запасов и т.д.). Таким образом, разность (xi – ói) ñî-

399

ставляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Предполагаем, что бала нс составляется в стоимостном разрезе. Обозначим через xik часть продукции i-й отрасли, которая потребляется k-й отраслью, для обеспечения выпуска ее продукции в размере xi.

Очевидно, величины, расположенные в строках, связаны следующими балансовыми равенствами:

Отсюда стоимостной баланс в общем виде запишется уравнениями:

k=1

Рассмотрев отношение количества продукции i-й отрасли, поступающей в k-ю отрасль для обеспечения выпуска ее продукции в размере xk, получим затраты на единицу валовой продукции

400