шапкин задачи с решениями

При ограничениях

найти максимум линейной функции

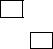
Геометрическое решение задачи

Поскольку задача двухмерная, то ее можно решить графическ и. Система ограничений (7.1) дает многоугольник решений. Для его построения проводим прямые, являющиеся границами мно -

гоугольника и с помощью пробной точки, например (0; 0), определим полуплоскости, задаваемые этими прямыми (рис. 86):

l1: 13x1 + 24x2 = 312, l2: 32x1 + 32x2 = 480, l3: 58x1 + 29x2 = 696, l4: x1 + x2 = 10.

В пересечении соответствующих полуплоскостей получим ш е- стиугольник ABCDEF.

371

Для нахождения max z построим из начала координат вектор n = (4; 3) и перпендикулярную ему линию уровня z = 0, т.е. пря-

ìóþ 4x1 + 3x2 = 0.

Далее передвигаем линию уровня z = const в направлении возрастания z, т.е. параллельно самой себе в направлении вектора n . В последней пересекаемой вершине D получаем наибольшее зна- чение z. Вершина D — это точка пересечения прямых l2 è l3.

Находим координаты точки D из системы:

Решая систему, найдем, что х1 = 9, õ2 = 6, ò.å. D (9; 6) è ïðè ýòîì z = 4 · 9 + 3 · 6 = 54 (óñë. åä.).

Для решения задачи симплекс — методом приведем систему ограничений (7.1) к форме равенств с помощью неотрицательны х дополнительных переменных yi (i = 1, 2, 3, 4):

Так как в I — столбце есть отрицательный элемент, то его нужно сделать положительным. Выбираем у4 — строку с отрицательным свободным членом «–10».

372

В этой же строке есть отрицательные элементы, выбираем ка - кой-нибудь из них, например, «–1» в х1 — столбце. И х1 — столбец принимаем в качестве разрешающего столбца.

Делим свободные члены на соответствующие элементы разре - шающего столбца, получаем {24, 15, 12, 10} и наименьшее положительное отношение будет соответствовать разрешающей строке, следовательно, у4 — строка является разрешающей, а элемент –1 разрешающим элементом. Совершаем шаг модифицированного жорданова исключения (ШМЖИ) с разрешающим элементом –1 по правилу:

1)на месте разрешающего элемента стоит величина ему обратная;

2)элементы разрешающей строки делятся на разрешающий элемент;

3)элементы разрешающего столбца делятся на разрешающий элемент и знак меняется;

4)остальные элементы новой таблицы находятся по формуле прямоугольника [17, стр. 52]:

Получаем табл. 7.2, при этом переменные х1 è y4 меняются местами. Из таблицы видно, что свободные коэффициенты в I — столбце не отрицательны, следовательно, получено опорное ре-

шение: х1 = 10, õ2 = 0, y1 = 182, y2 = 5, y3 = 4, y4 = 0, Z = 40. Геометрически это означает, что мы находимся в вершине F (10;0) мно-

гоугольника решений ABCDEF.

Ò à á ë è ö à 7.2

373

Это решение не является оптимальным, так как в Z — строке имеется отрицательный коэффициент, улучшаем план.

Выбираем разрешающий элемент по правилу: выбираем столбец с наименьшим отрицательным элементом в z-строке — разрешающий столбец, делим свободные члены в I-столбце на соответствующие коэффициенты и наименьшее положительное отнош е- ние соответствует разрешающей строке. На пересечении сто ит разрешающий элемент 2 . Совершая ШМЖИ с разрешающим элементом 2 по выше приведенному правилу, получаем табл. 7.3.

Ò à á ë è ö à 7.3

Решение, получаемое из табл. 7.3, также не является оптимальным, так как в Z-строке имеется отрицательный коэффи-

374

совершая ШМЖИ, приходим к табл. 7.4, в которой все коэффициенты в Z-строке неотрицательны, а, следовательно, max Z уже достигнут и ему соответствует решение х1 = 9, õ2 = 6, ïðè ýòîì

Zmax = 54 (óñë. åä.).

Ответ: максимальная прибыль Z = 54 (усл. ед.) достигается при изготовлении 9 единиц изделий I и 6 единиц изделий II.

7.1.2. Транспортная задача

Это задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пунктов произ водства (станций отправления) в пункты потребления (станции назначения).

Транспортная задача является важнейшей частной моделью линейного программирования, имеющей обширные практичес кие приложения не только к проблемам транспорта. Особо важное значение она имеет в деле рационализации поставок важней ших видов промышленной и сельскохозяйственной продукции, а т акже оптимального планирования грузопотоков и работы разл ич- ных видов транспорта.

7.1.2.1.Постановка задачи

èее математическая модель

Некоторый однородный продукт производится в m пунктах произâîäñòâà À1, À2, …, Àm. Задан объем производства аi пункта Ai (i = 1, m). Произведенный продукт должен быть перевезен в n пунктоâ потребления B1, B2, …, Bn. Известен спрос bj пункта B j ( j = 1, n) . Заданы также транспортные издержки Сij, связанные с перевозкой единицы продукта из пункта Аi в пункт Вj. Требуется составить план перевозок, обеспечивающий при минималь ных транспортных расходах (издержках) удовлетворения спроса всех пунктов потребления за счет продукта, произведенного во в сех пунктах производства.

Обозначим через хij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю. Тогда условие задачи можно записать в виде табл. 7.5, которую в дальне й- шем будем называть матрицей планирования.

375

Различают задачи с закрытой моделью, когда åai = åbj è

открытой моделью, когда åai ¹ åbj , т.е. баланс между запасами и потребностями отсутствует.

376

Необходимым и достаточным условием разрешимости транспортной задачи является равенство суммарных запасов сум мар-

Математическая модель транспортной задачи относится к з ада- чам линейного программирования и может быть решена симпл ексным методом. Однако ввиду исключительной практической ва жности этой задачи и специфики ограничений (7.5) — (7.7): ограничени я заданы в виде уравнений; каждая неизвестная входит лишь в два уравнения, коэффициенты при неизвестных — единицы, для ее реше ния созданы специальные алгоритмы. Самым распространенным м етодом решения транспортной задачи является метод потенциа лов.

Решение транспортной задачи разбивается на два этапа:

1.Определение начального допустимого базисного решения ( первого опорного плана) — первоначальное распределение пост авок.

2.Построение последовательных итераций (шагов), улучшающих опорные планы (каждый новый план не должен увеличи- вать суммарные затраты).

После выполнения первого этапа шаги второго этапа проводятся до тех пор, пока не будет найдено оптимальное распре деление поставок.

7.1.2.2.Построение первоначального опорного плана

Рассмотрим два метода построения первого опорного плана . План составляется последовательным заполнением по одно й клетке в таблице перевозок так, что каждый раз либо полнос тью удовлетворяется потребность одного из потребителей, либ о полностью ввозится груз от некоторого поставщика. В теории д ока-

377

зывается, что базисное решение системы ограничений (из m + n уравнений с mn переменными) в условиях транспортной задачи имеет m + n – 1 базисных переменных (ее ранг равен m + n – 1), поэтому, совершив m + n – 1 указанных шагов, получим первый опорный план. Различие двух методов отыскания первого опо р- ного плана состоит в различии способов выбора последоват ельности заполнения клеток.

Диагональный метод или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного пл а- на заполняется верхняя левая клетка («северо-западный уг ол») оставшейся части таблицы. При таком методе заполнение таб - лицы начинается с клетки переменного х11 и заканчивается в клетке неизвестного хmn, т.е. идет как бы по диагонали таблицы перевозок.

Метод наименьшей стоимости. Исходное опорное решение, построенное диагональным методом, как правило, оказывает ся весьма далеким от оптимального, так как при его определен ии совершенно игнорируются величины затрат сij. Поэтому требуются в дальнейших расчетах много итераций для достижения оптимального плана. Число итераций можно сократить, если ис ходный план строить по более рациональному правилу «минимал ь- ного элемента». Сущность его состоит в том, что на каждом ша ге заполняется клетка с наименьшей величиной сij. Если такая клетка не единственная, то лучше заполнять ту, по вертикали или горизонтали которой встречаются большие сij, а в принципе заполняется любая из них.

Пусть это будет клетка (i, j). Запишем в эту клетку хij = min (ai, bj). Åñëè ai < bj, то запасы поставщика Аi исчерпаны, а потребность Вj

стала b′j = bj − ai . Поэтому, не принимая более во внимание i-ю

строку, снова ищем клетку с наименьшей стоимостью перевоз ок и заполняем ее с учетом изменившихся потребностей. Для сл учая ai > bj из рассмотрения исключается j-й столбец, а запасы Аi ïîëà-

гаются равными ai′ = ai − bj . Продолжаем этот процесс до тех пор,

пока все запасы не будут исчерпаны, а все потребности — удо в- летворены. Необходимо отметить, что при наличии в таблице клеток с одинаковыми тарифами, планы, полученные с помощь ю этого метода, могут быть разными, однако они, несомненно, бл и- же к оптимальному, чем план, составленный по методу северо - западного угла.

378

Прежде чем перейти к анализу оптимальности планов и способам их улучшения, выясним, каким требованиям должны удо в- летворять составляемые планы. Для этого вернемся к систем е ограничений (7.5) — (7.7). Очевидно, что первая группа уравнений требует, чтобы сумма элементов плана по i-й строке равнялась аi,

i = 1, m; а вторая группа — чтобы сумма элементов по j-му столб-

цу была равна bj, j =1, n. Условие закрытости модели транспортной задачи означает, что среди m + n уравнений системы ограни- чений независимых только m + n – 1, поэтому в любом базисном решении этой системы должно быть m + n – 1 базисных переменных. Поскольку свободные переменные в таком решении равны нулю, то в транспортной таблице им будут соответствовать пустые клети.

Клетки таблицы, в которых записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свобод - ными.

В теории доказано, что базисное решение системы ограниче- ний (7.5) — (7.7) в условиях транспортной задачи должно иметь m + n – 1 базисных переменных.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n – 1.

Если на каком-то этапе решения получился вырожденный план, то его необходимо пополнить, проставив в недостающе м числе клеток 0 и тем самым объявив их базисными. Поскольку этим дополнительным клеткам будут отвечать нулевые пере возки, то общий баланс и суммарная стоимость перевозок плана при этом не изменится. Однако проводить пополнение плана, выб и- рая клетки произвольно, нельзя. Приведем условия, которым должен соответствовать пополненный план.

Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две с о- седние вершины ломаной были расположены либо в одной стро - ке, либо в одном столбце. Ломаная может иметь точки самопер е- сечения, но не в клетках цикла.

План называется ациклическим, если его базисные клетки не содержат циклов.

Доказано, что оптимальные планы являются ациклическими, поэтому и первоначальный план также должен удовлетворят ь этому требованию. Заметим, что планы, полученные с помощью ме-

379

тодов северо-западного угла и наименьшей стоимости, ацикл и- ческие. Однако если план оказался вырожденным, то при его п о- полнении требование ацикличности необходимо учитывать.

7.1.2.3. Оптимальность базисного решения. Метод потенциалов

Получив первый опорный план, следует проверить его оптимальность и, если требуется, перейти к новому опорному пла ну с лучшим значением целевой функции Z. Для этого применяют метод потенциалов. Каждому поставщику Аi и каждому потребителю Вj сопоставляют, соответственно, величины Ui è Vj — потенциалы этих пунктов.

Для того чтобы некоторый опорный план X* = || xij* || транспортной задачи был оптимальным, необходимо и достаточно,

чтобы ему соответствовала система из (m + n) чисел Ui*, Vj*, удовлетворяющих условиям:

(для занятых клеток) и

(для свободных клеток).

ЧислаUi*, Vj*, называются потенциалами соответственно про-

изводителей и потребителей, вся их система — потенциально й, а условия (7.8) — (7.9) — условиями потенциальности системы

{Ui*, Vj*}; каждое в отдельности неравенство (равенство) называ-

ется условием потенциальности для соответствующей клет киi(, j). Поскольку число неизвестных потенциалов (m + n) всегда на единицу больше числа уравнений (числа заполненных клеток) N = m + n – 1, то выбираем строку, где есть занятая клетка и для этой строки назначаем потенциал равным нулю, например U1 = 0, и легко находим последовательно из уравнений (7.8)

значения остальных потенциалов.

Если же число заполненных клеток N < m + n – 1, то вводим дополнительно необходимое количество занятых клеток с н уле-

380