шапкин задачи с решениями

Пример 6.37. При уровне значимости α = 0,05 проверить гипотезу о нормальном распределении генеральной совокупн ости, если известны эмпирические и теоретические частоты:

Решение. Число различных вариант m равно 7, значит число степеней свободы распределения χ 2 равно 7 – 3 = 4. По таблице критических точек распределения χ 2, по уровню значимос-

Пример 6.38. Дано статистическое распределение выборки:

341

Решение.

1.Найдем методом произведений выборочные: среднюю, дисперсию и среднее квадратическое отклонение. Воспользуем ся методом произведений, для чего составляем табл. 1.

Ò à á ë è ö à 1

В качестве ложного нуля принимаем С = 5,8 — варианта с наибольшей частотой 35. Шаг выборки h = x2 – x1 = 3,0 – 1,6 = 1,4. Тогда условные варианты определяем по формуле

Контроль: 339 = 189 + 2 · 25 + 100.

Вычисления произведены верно. Найдем условные моменты.

342

Вычисляем выборочную среднюю:

x = M1 ×h +C = 0,25×1,4 + 5,8 = 6,15.

Находим выборочную дисперсию:

d = [M2 - (M1 )2 ]× h2 = [1,89 - (0,25)2 ]×1,42 = 3,58.

Определяем выборочное среднее квадратическое отклонени е:

σ = d = 3,58 = 1,89.

2.Строим нормальную кривую.

Для облегчения вычислений все расчеты сводим в табл. 2.

Заполняем первые три столбца.

В четвертом столбце записываем условные варианты по формуле, указанной в «шапке» таблицы. В пятом столбце находим значения функции

343

и заполняем последний столбец. Отметим, что в последнем ст олбце частоты ni′ округляются до целого числа и åni′ = åni =100.

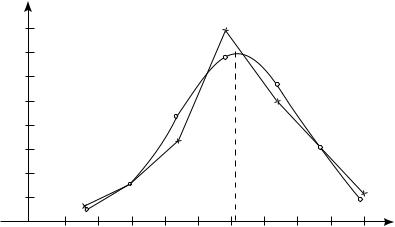
В системе координат (xi ; yi = ni′ ) строим нормальную (теоретическую) кривую (рис. 81) по выравнивающим частотам ni′ (îíè

отмечены кружками) и полигон наблюдаемых частот (они отме - чены крестиками). Полигон наблюдаемых частот построен в с истеме координат (xi; yi = ni).

344

3. Проверяем гипотезу о нормальности X при уровне зна- чимости α = 0,05.

Вычислим χíàáë2 ., для чего составим расчетную таблицу 3.

åni2 − å ni = 102,78 −100 = 2,78. ni′

Совпадение результатов подтверждает правильность вычис - лений.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариантов) 7. ν = 7 – 3 = 4.

По таблице критических точек распределения χ 2, по уровню зна- чимости α = 0,05 и числу степеней свободы ν = 4 находим χêð2 . = 9,5.

Òàê êàê χíàáë2 . < χêð2 . то нет оснований отвергать нулевую гипотезу. Другими словами, расхождение эмпирических и теоре ти-

ческих частот незначимое. Следовательно, данные наблюден ий согласуются с гипотезой о нормальном распределении гене ральной совокупности.

345

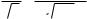
4. Найдем доверительный интервал для оценки неизвестного МО М (Х), полагая, что Х имеет нормальное распределение, среднее квадратическое отклонение σ = σ Õ = σ Â = 1,89 и доверительная вероятность γ = 0,95.

Известен объем выборки: n = 100, выборочная средняя xÂ= 6,15. Из соотношения 2Φ (t) = γ получим Φ (t) = 0,475. По таблице

находим параметр t = 1,96. Найдем точность оценки

δ = tσ = 1,96×1,89 = 0,37. n 100

Доверительный интервал таков:

x -δ < M(X ) < x + δ

или 6,15 – 0,37 < М (Х) < 6,15 + 0,37 5,78 < М (Х) < 6,52. Надежность γ = 0,95 указывает, что если произведено доста-

точно большое число выборок, то 95% из них определят такие доверительные интервалы, в которых параметр действитель но заключен.

6.7. Элементы теории корреляции

Корреляционный анализ — широко известный и эффективный метод математической статистики, позволяющий по совокуп ности значений показателей выявлять и описывать связи между показателями.

Если каждому значению величины Х соответствует несколько значений величины У, но число этих значений, как и сами значе- ния, остается не вполне определенным, то такие связи назыв аются статистическими. Например, уровень производительност и труда на предприятиях тем выше, чем больше его электровооруж енность. Вместе с тем, нет никаких оснований утверждать об однозначности этой зависимости.

Если изменение одной из переменных сопровождается изменениями условного среднего значения другой переменной в ели- чины, то такая зависимость является корреляционной.

Под условным средним yX подразумевают среднее арифмети- ческое значений У, соответствующих значению Х = х. Например,

346

пусть при х1 = 2 величина У приняла значения у1 = 5, y2 = 6 è ó3 = 10. Тогда условное среднее равно

Корреляционной зависимостью У от Х называют функциональную зависимость условной средней yÕ îò õ: yÕ = f (x). Это уравнение называют уравнением регрессии У на Х; функцию f (x) называют регрессией У на Х, а ее график — линией регрессии У на Х.

Корреляционный анализ рассматривает две основные задач и. Первая задача теории корреляции — установить форму корреляционной связи, т.е. вид функции регрессии (линейная, кв ад-

ратичная и т.д.).

Вторая задача теории корреляции — оценить тесноту (силу) корреляционной связи.

Теснота корреляционной связи (зависимости) У на Х оценивается по величине рассеивания значений У вокруг условного среднего. Большое рассеивание свидетельствует о слабой завис имости У от Х, малое рассеивание указывает на наличие сильной зависимости.

6.7.1. Отыскание параметров выборочного уравнения прямой линии регрессии

по несгруппированным данным

Пусть количественные признаки Х и У связаны линейной корреляционной таблицей и в результате независимых испытан ий получены n пар чисел:

Выборочное уравнение прямой линии регрессии У на Х выбираем в виде:

ó = ρyx · x + Â.

347

Параметры ρyx и В, которые определяются методом наименьших квадратов, имеют вид:

Величина r Â= ρ yx σ x — называется выборочным коэффициен-

σ y

том корреляции. Она служит для оценки тесноты линейной ко р- реляционной зависимости.

Абсолютная величина выборочного коэффициента корреляции не превосходит единицы, т.е. –1 ≤ r ≤ 1.

С возрастанием | r | линейная корреляционная зависимость становится более тесной и при | r | = 1 переходит в функциональную.

6.7.2. Отыскание параметров выборочного уравнения прямой линии регрессии

по сгруппированным данным

При большом числе испытаний одно и то же значение Х может встретиться nx раз, одно и то ж значение У может встретиться nó раз и одна и та же пара чисел (x; y) может встретиться nxy ðàç,

причем обычно å nx = å ny = å nxy = n — объем выборки.

Поэтому данные наблюдений группируют, т.е. подсчитывают nx, ny, nxy. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Если обе линии регрессии У на Х и Х на У — прямые, то кор-

ãäå yx — условная средняя; x è y — выборочные средние признаков Х и У; σ x è σ ó — выборочные средние квадратические отклонения; r — выборочный коэффициент корреляции.

348

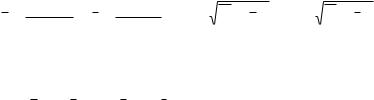
Выборочное уравнение прямой линии регресии Х на У имеет вид:

Считаем, что данные наблюдений над признаками Х и У заданы в виде корреляционной таблицы с равноотстоящими вариа н- тами.

Тогда переходим к условным вариантам:

Тогда выборочный коэффициент корреляции

Зная эти величины, найдем параметры, входящие в уравнения регрессии, по формулам

x = h1 ×u + C1; y = h2 ×v +C2 ; σ x = h1 σ u ; σ y = h2 σ v .

349

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ ПО РАЗДЕЛУ 6

12.1.Случайные события

12.1.1.В ящике находятся 6 одинаковых пар перчаток черного цвета и 4 одинаковых пары перчаток бежевого цвета. Найти ве - роятность того, что две наудачу извлеченные перчатки обра зуют пару.

Решение. Рассмотрим событие А — две извлеченные наудачу перчатки образуют пару; и гипотезы: В1 — извлечена пара перча- ток черного цвета, В2 — извлечена пара перчаток бежевого цвета, В3 — извлеченные перчатки пару не образуют.

Вероятность гипотезы В1 по теореме умножения равна произведению вероятностей того, что первая перчатка черного цв ета и вторая перчатка черного цвета, т.е.

P (B1 ) = P1÷åð. ×P2 ÷åð. = 1220 ×1911 = 3395 .

Аналогично, вероятность гипотезы В2 равна:

P (B2 ) = P1áåæ. ×P2 áåæ. = 208 ×197 = 1495 .

Так как гипотезы В1, Â2 è Â3 составляют полную группу событий, то вероятность гипотезы В3 равна:

По формуле полной вероятности имеем:

P (A) = P (B1 )×PB1 (A) + P (B2 )×PB2 (A) + P (B3 )×PB3 (A),

ãäå PB2 (A) есть вероятность того, что пару образуют две черные перчатки и PB1 (A) = 1; PB2 (A) — вероятность того, что пару об-

разуют две бежевые перчатки и PB2 (A) =1; и, наконец, PB3 (A) — вероятность того, что пару образуют перчатки разного цвет а и PB3 (A) = 0.

350