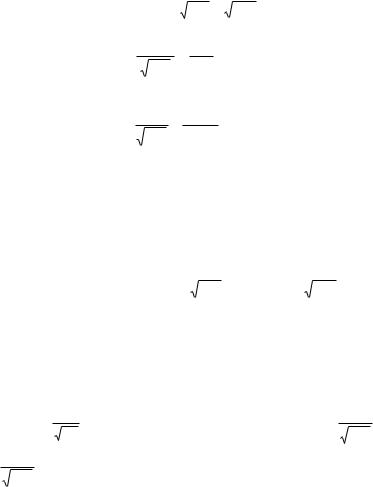
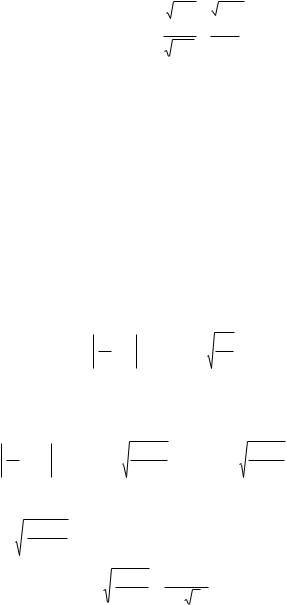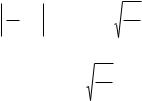Пример 6.21. С конвейера сходит в среднем 85% изделий первого сорта. Сколько изделий необходимо взять, чтобы с веро ятностью 0,997 отклонение частости изделий первого сорта в них от 0,85 по абсолютной величине не превосходило 0,01?
Решение. Здесь p = 0,85, q = 1 – 0,85 = 0,15, ε = 0,01, P = 0,997,
n — ? Так как в равенстве |
P |
æ |
m |
- p |
ö |
æ |
ε |
n |
ö |
известна |
ç |
|
< ε ÷ |
» F ç |
|
÷ |
|
|
ç |
n |
|
÷ |
ç |
|
|
÷ |
|
|
|
è |
|
ø |
è |
|
pq ø |
|
вероятность P, стоящая слева, то сначала решим уравнение Φ (t) = P.
Пусть tP — корень этого уравнения. Тогда ε n » tP , |
ε 2 |
n |
≈ tP2 |
|
|
|
|
|
|
|
|
pq |
|
pq |
|
|
|
pqt2 |
|
|
|
|
|
|
и, следовательно, |
n » |
P |
. Для нашего случая t0,997 = 3, поэтому |
|
|
|
|
ε 2 |
|
|
|
|
|
|
|
n » |
0,85×0,15×32 |
= |
1,1475 |
=11475. |
|
|
|
|
|
|
|
|
|
|
|
|
(0,01)2 |
0,0001 |
|
|
|
6.3. Случайные величины
Случайная величина (СВ) — это переменная, принимающая в каждом конкретном испытании конкретное числовое значен ие, которое может меняться от опыта к опыту.
Примеры: количество клиентов, посетивших парикмахерскую за день; месячная прибыль ателье; время проявления фотопл енки.
Случайные величины представляют результаты измерений в случайных экспериментах (испытаниях). Существует два вид а слу- чайных величин: дискретные и непрерывные.
Дискретные случайные величины — это переменные, принимающие только отделенные друг от друга числовые значения (которые можно заранее перечислить).
Примеры: оценки в зачетной книжке (3, 4, 5); количество студентов на экзамене.
Непрерывная случайная величина может принимать любые значения из замкнутого или открытого интервала. Например , размеры одной и той же детали, определяемые разными людьми ил и с применением разных инструментов, различны.
Возможны комбинированные (дискретно-непрерывные) слу- чайные величины, которые на одних интервалах являются неп рерывными, а на других — дискретными.


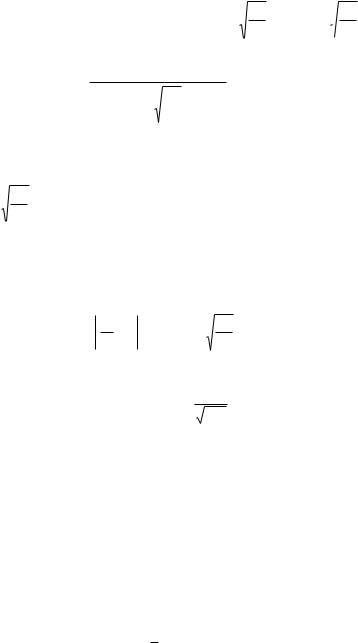


 210 =14,491
210 =14,491