шапкин задачи с решениями

Тогда с учетом bm = 0 ряд Фурье получает вид:

10.ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

10.1.Действия с комплексными числами

10.1.1.Выполнить действия:

a) (4 + i · 5)2 · (5 – i · 4) = (16 + 40 · i + 25 · i2) · (5 – 4 · i) = =(–9 + 40 · i) (5 – 4i) = –45 + 200 · i + 36 · i + 160 = 115 + 236 · i.

10.2.1. Показать, что функция f (z) = (z + 4)2 + z – 5 · i аналитична.

Представим функцию f (z) в виде u (x, y) + i · v (x, y), где z = x + i · y. Получаем

f (z) = (x + i · y + 4)2 + x + i · y – 5i =

=(x + 4)2 + 2 · (x + 4) · y · i – y2 + x + i · y – 5i = =(x + 4)2 + x – y2 + i · (2 (x + 4) · y + y – 5).

Тогда u (x, y) = (x + 4)2 + x – y2, v (x, y) = 2(x + 4) · y + y – 5. Проверим выполнение для f (z) условий Коши – Римана:

281

Получаем, что

Следовательно, условия Коши – Римана выполнены и данная функция f (z) – аналитична.

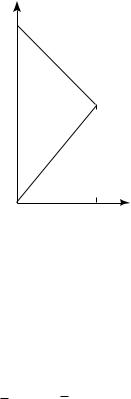
10.3.1. Вычислить ò ((5x - y) + i ×(x + 4 × y)) dz, где контур С —

где общий интеграл по контуру С = ОАВ разобьем на два контура

ÎÀ è ÀÂ.

Уравнение ОА: y = 54 x, dy = 54 ×dx. Äëÿ ÀÂ: y = 9 – x, dy = –dx.

282

Тогда

ò f (z)×dz = ò (5x - y)×dx - (x + 4y)×dy + i × ò (x + 4y)×dx + (5x - y)×dy =

Аналогично,

ò (5x - y)× dx - (x + 4y)× dy + i × ò (x + 4y)× dx + (5x - y)× dy =

точки z0 = 0 в ряд Тейлора и найти радиус сходимости ряда. Представим данную функцию в виде суммы элементарных

дробей

283

Разложим каждую из этих функций в ряд по степеням z – z0 = = z – 0 = z c помощью геометрической прогрессии:

Область сходимости каждой из прогрессий есть | z | < 4 и | z | < 9. Общая часть дает радиус сходимости равный R = 4 или | z | < 4.

и найти вычеты в них.

Разложим данную функцию в ряд Лорана по степеням z:

Это разложение верно при | z | < 5. Следовательно, данная функция имеет точку z0 = 0 полюсом второго порядка. Вычетом этой функции f (z) относительно полюса z0 = 0 является коэффициент

стей z – (–5) = z + 5 получим, что точка z1 = –5 будет полюсом

284

11.2.1. Решить операционным методом дифференциальное уравнение: x² – x¢ – 20 · x = e–t, x (0) = 0, x¢ (0) = 4.

Решение. Переходим от оригиналов к изображениям функций.

Пусть x (t) ÉX( p) = x,

x¢ (t) É p× X( p) - x0 = p×X - 0 = p× X, x¢¢ (t) É p2 ×X( p) - p× x0 - x0¢ = p2 × X - 4.

Тогда с учетом того, что изображение правой части есть e−t É p1+1, получим операторное уравнение в виде:

Пользуясь таблицей изображений, находим искомое частное

решение:

x (t) = -181 × e−t + 2554 × e5t - 1127 × e−4t.

285

РАЗДЕЛ 6

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

6.1. Основные понятия и теоремы теории вероятностей

6.1.1. Классическое определение вероятности

Если испытание может привести к одному и только к одному из n различных равновозможных исходов (называемых элементарными исходами) и если m из этих исходов благоприятствуют появлению событий А, то вероятность события А определяется формулой

Это — классическое определение вероятности. Отметим основные свойства вероятности.

1. Вероятность любого события заключена между нулем и единицей:

0 ≤ P (A) ≤ 1.

2. Вероятность достоверного события I, т.е. такого события, которое при испытании обязательно произойдет, равна един ице:

P(I) = 1.

3.Вероятность невозможного события О, т.е. события, которое в результате испытания не может произойти, равна нулю :

P(Î) = 0.

4.Сумма вероятностей двух противоположных событий А и

À, т.е. таких событий, что появление одного из них исключает появление другого, равна единице:

P (A) + P (A) = 1.

286

Пример 6.1. Из урны, в которой находится 4 белых, 9 черных и 7 красных шаров, наугад вынимают один шар. Какова вероятнос ть появления белого шара?

Решение. Здесь элементарным исходом является извлечение из урны любого шара. Число всех таких исходов равно числу шар ов в урне, т.е. n = 20. Число исходов, благоприятствующих появлению белого шара (событие А), очевидно, равно числу белых шаров в урне, т.е. m = 4. Поэтому по формуле (1) находим:

P (A) = 204 = 51 .

Пример 6.2. Игральный кубик бросают два раза. Какова вероятность того, что сумма выпавших очков окажется равной во сьми?

Решение. Обозначим через Aij событие, состоящее в том, что при первом подбрасывании выпало i очков, а при втором – j оч- ков. Тогда 36 событий

A11, A12 , K, A16;

A21, A22 , K, A26;

K, K, K, K,

A61, A62 , K, A66

можно рассматривать как элементарные исходы опыта. Следо вательно, число всех элементарных исходов n = 36. Появлению события А (сумма выпавших очков равна восьми) благоприятству-

ют исходы А26, À35, À44, À53, À62. Таким образом, m = 5. Отсюда получаем: 5

P (A) = 36 .

6.1.2. Геометрические вероятности

Если результат испытания определяется случайным положе нием точки в некоторой области, причем положения точек в этой о бласти равновозможны, то вероятность события находится по форму ле

где S – геометрическая мера (длина, площадь или объем) всей области, S0 – геометрическая мера той части области, попадание в которую благоприятствует данному событию.

287

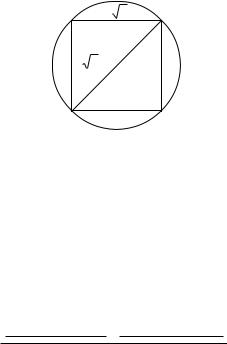
Пример 6.3. В круг вписан квадрат. Какова вероятность того, что точка, наудачу поставленная в круге, окажется внутри к вадрата?

Решение. Площадь круга S = πr2, площадь квадрата S0 = 2r2, где r – радиус круга (рис. 69). Отсюда по формуле (2) находим искомую вероятность:

r

r 2 ∙0

Ðèñ. 69

Пример 6.4. Известно, что телефонный звонок должен последовать от 11 ч до 11 ч 30 мин. Какова вероятность того, что звонок произойдет в последние 10 минут указанного промежутка , если момент звонка случаен?

Решение. Воспользуемся геометрической схемой. Для этого промежуток времени от 11 ч до 11 ч 30 мин представим в виде отрезка АВ длиной в 30 единиц, а промежуток времени от 11 ч 20 мин до 11 ч 30 мин – в виде отрезка СВ длиной в 10 единиц (рис. 70). Слу-

чайный звонок в некоторый момент рассматриваемого получаса изображается наугад взятой точкой на отрезке АВ. Тогда вероятность того, что звонок произойдет в интервале от 11 ч 20 мин до 11 ч 30 мин, в полученной схеме означает вероятность того, что

288

точка, наугад взятая на отрезке АВ, окажется принадлежащей отрезку СВ. Эта вероятность, очевидно, равна:

p = 1030 = 13 .

Пример 6.5. В любой момент времени промежутка Т равновозможны поступления в приемник двух сигналов. Приемник с чи- тается забитым, если разность по времени между сигналами меньше τ < T. Какова вероятность того, что приемник будет забит?

Решение. Рассмотрим прямоугольную декартову систему координат хОу. Пусть х и у – моменты поступления в приемник соответственно первого и второго сигналов. Тогда все возможны е комбинации поступления сигналов изобразятся точками квадрата 0 ≤ õ ≤ Ò, 0 ≤ ó ≤ Т. Так как моменты поступления сигналов равновозможны в течение промежутка времени Т, то положения точек (х; у) в области рассматриваемого квадрата также равновозможн ы.

Выясним, какие точки квадрата благоприятствуют интересующему нас событию А (приемник забит). Событие А может произойти лишь в том случае, если разность по времени между си гналами будет меньше τ ò.å. åñëè

Таким образом, область квадрата, благоприятствующая собы - тию А (на рис. 71 она заштрихована), состоит из точек, координаты (х; у) которых удовлетворяют неравенству (*).

Ðèñ. 71

289

Площадь квадрата S = T2; площадь заштрихованной области

6.1.3. Теоремы сложения и умножения вероятностей

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением нескольких событий называется событие, со - стоящее в совместном осуществлении всех этих событий.

Теорема сложения вероятностей. Если события А1, À2, … , Àn несовместны, т.е. никакие два из них не могут осуществиться вместе, то

Вероятность события А, вычисленная в предположении, что произошло событие В, называется условной вероятностью события А при условии В и обозначается Р (А / В).

Теорема умножения вероятностей. Вероятность произведения нескольких событий равна произведению вероятности одно го из них на условные вероятности всех остальных, причем вероят ность каждого последующего события вычисляется в предположен ии, что все предыдущие события уже произошли:

P(À1 · À2· À3… Àn) =

=P (À1) · P (À2 / À1) · P (À3 / À1 À2) … P (Àn / À1 À2 … Àn – 1). (4)

Если события А1, À2, … , Àn независимы, т.е. осуществление любого числа из них не меняет вероятностей осуществления остальных, то

290