Закон всемирного тяготения Ньютона

Две материальные точки с массами и, находящиеся на расстояниидруг от друга притягиваются друг к другу с силой

,

где -гравитационная постоянная.

В общем случае двух тел произвольной формы можно мысленно разбить их на малые элемен-ты и просуммировать силы взаимодействия между ними:

.

Таким образом можно, например, показать, что сила гравитационного взаимодействия между двумя однородными шарами с массами ,и расстоянием между центрамиравна

.

Из закона всемирного тяготения следует, что любая материальная точка создает вокруг себя силовое (гравитационное) поле, действующее на другие материальные точки. Оно относится к классу так называемых центральных полей, для которых сила может быть представлена в виде:

,

где - радиус-вектор, проведенный из точки, называемой центром силового поля, в данную точку.

Рассмотрим одно важное свойство движения в центральном поле. Для момента количества движения материальной точки в этом случае имеем:

, или .

Таким образом, при движении материальной точки в гравитационном поле, создаваемом другой материальной точкой, сохраняется момент количества движения .

Отсюда следует, что траектория движения материальной точки в центральном поле целиком лежит в плоскости перпендикулярной вектору (плоская кривая, рис. 3). Такими кривыми являются траектории движения планет вокруг Солнца и траектории искус-ственных спутников Земли.

Потенциальная энергия частицы в гравитационном поле.

Проекция силы потенциального поля на направление связана с потенциальной энергией соотношением (лекция 5)

.

Выберем в качестве направление радиуса-вектораот материальной точкик мате-риальной точке. Тогда

.

Отсюда, полагая , получим

.

На основании анализа наблюдений положения планет, проведенных Тихо Браге, Кеплер сформулировал законы их движения.

Законы Кеплера.

1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

2. Радиус-вектор планеты в равные времена описывает равные площади.

3. Квадраты времен обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца.

Законы Кеплера можно получить с помощью 2-го закона Ньютона и закона всемирного тяготения.

1-ый закон Кеплера.

Т

ак как траектория планеты является плоской, сначала введем в этой плоскости декартову систему координатс началом в Солнце. Однако, оказалось, что уравнения движения планеты удается проинтегрировать до конца лишь в так называемых полярных координатах,связанных с декартовыми соотношениями (рис. 3)

, .

При движении планеты вокруг Солнца сохраняются ее полная энергия и проекция момента количества движения на ось . В полярных координатах эти законы сохранения имеют вид:

,

.

Здесь точками обозначены производные по времени, - масса планеты, - масса Солнца. Интегрируя эти уравнения можно показать, что при траектория является эллипсом, то есть выполняется 1-ый закон Кеплера. При траектория представляет собой гиперболу, а при - параболу.

Вообще существует два вида движения в гравитационном поле. При инфинитном движении материальная точка может удалиться сколь угодно далеко от ее начального положения. В случае финитного движения траектория не может выйти за пределы некоторой ограни-ченной области пространства. При траектория всегда будет финитной, так как при полная энергия , что противоречит исходному предположению. При является инфинитной.

2 – ой закон Кеплера.

Этот закон является следствием сохранения момента импульса, так как площадь описы-ваемая радиусом-вектором планеты в единицу времени

.

3 – ий закон Кеплера.

Его легко получить для частного случая движения по окружности:

.

Космические скорости.

1-ая космическая скорость – скорость тела, движущегося вблизи поверхности Земли по финитной траектории:

.

2-ая космичская скорость – скорость тела вблизи поверхности Земли, движущегося под действием ее поля тяготения по инфинитной траектории:

.

3 – я космическая скорость – скорость тела вблизи поверхности Земли, движущегося по траектории инфинитной по отношению к Солнцу. В зависимости от положения Земли она варьируется в интервале примерно от до.

ЛЕКЦИЯ 24

Упругие свойства жидкостей и газов.

Г

азы и жидкости обладают объемной упругостью но не оказывают сопротивления дефор-мации сдвига. В состоянии равновесия напряжение в жидкости или газе (его в этом случае принято называть давлением) всегда нормально к площадке, на которую оно действует.Давление определяется как предел отношения (см. рис. 1)

.

Здесь - сила, действующая со стороны окружающей жидкости на малую площадку. Давление является скалярной величиной, так как оно не зависит от ориентации этой площадки.

Жидкости малосжимаемы. Поэтому для описания многих явле-ний часто используется модель абсолютно несжимаемой жидкости. При движении жидкости в ней могут возникать силы вязкого трения. Идеальная жидкость – при любых движениях силами вязкости можно пренебречь.

Законы гидростатики.

1. Закон Паскаля.

Если нет внешних объемных сил, то в равновесии давление жидкости постоянно во всем объеме.

2. Давление жидкости, находящейся в равновесии в поле тяжести.

Из условия равновесия мысленно выделенного вертикального цилиндра внутри жидкости с плотностью легко получить

.

3. Закон Архимеда.

На тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости (сила Архимеда).

С

ила Архимеда приложена к центру масс вытесненного объема (точкана рис. 3), называемогоцентром плавучести тела. Она возникает из-за того, что сила давления со стороны жидкости возрастает с глубиной. Взаимное расположение центра плавучести и центра масс определяют условия равновесия плавающих тел. Если центр масс при полном погружении тела в жидкость расположен ниже центра плавучести, то равновесие устойчиво. В этом случае при небольшом наклоне тела суммарный момент сил возвращает его в исходное положение. В противном случае суммарный момент приводит к увеличению угла наклона. Несколько сложнее обстоит дело при частичном погружении, что как раз чаще всего имеет место на практике. При

н

аклоне тела в этом случае изменяется форма вытесненного объема и положение центра плавучести (рис. 4). Если точка пересечения направления силы Архимеда и оси симметрии тела (точкана рис. 4) лежит выше центра масс, равновесие устойчиво, если ниже – неустойчиво. При этом центр масс может располагаться выше центра плавучести.

Рассмотрим общие условия равновесия при наличии объемных сил. Пусть на элемент жидкости с объемом действует внешняя сила. Величинаназываетсяплотностью объемных сил. Например, для жидкости с плотностью , находящейся в поле тяжести,. Выделим элемент жидкости в виде малого цилиндра, ось которого направлена вдоль оси, с площадью основанияи высотой. Тогда проекция на осьсил давления , дейст-вующих на цилиндр равна

.

Аналогичные выражения можно получить для проекций сил давления на оси и. Следовательно, полная сила разности давлений, действующая на элемент, может представлена в виде

, .

В состоянии равновесия (- внешняя объемная сила). Отсюда получаем

.

Это уравнение называется основным уравнением гидростатики.

П

ример. Равновесие жидкости во вращающемся сосуде.

Будем считать, что жидкость вращается вместе с сосудом. На элемент жидкости с объемом действуют сила тяжестии центробежная сила. Тогда полная объем-ная сила

.

Из уравнения гидростатики получаем

, ,.

При , отсюда получаем уравнение поверхности вращающейся жидкости(параболоид вращения).

ЛЕКЦИЯ 25

Стационарное течение жидкостей и газов.

Существует два основных метода описания течения жидкостей и газов (далее будем гово-рить только о жидкостях). Это метод Лагранжа, в котором задаются координаты и скорости каждой частицы жидкости, и метод Эйлера, в котором исследуется зависимость от коорди-нат и времени скорости потока жидкости . Мы будем вести рассмотрение в рамках метода Эйлера. Определим несколько важных понятий в таком описании.

Л

инии тока – линии, касательные к которым в каждой точке совпадают с направлением скорости жидкости (рис. 1). Густота линий тока пропорциональна скорости жидкости в данной части потока.

Трубка тока – часть жидкости, ограниченная линиями тока. Такое определение означает, что частицы жидкости никогда не пересекают стенок трубки тока.

Стационарное течение – скорость жидкости не зависит от времени в каждой точке пространства.

Р

ассмотрим тонкую трубку тока (по сечению трубки) в идеальной несжимаемой жидкости. При этом количество жидкости между двумя произвольными сечениямиидолжно оставаться постоянным. Следовательно, черезиза 1 сек должно проходить одинаковое количество жидкости, то есть

, или .

Э

то утверждение называетсятеоремой о неразрывности струи. Из него, в частности, следует, что если сечение трубки тока переменно, то жидкость движется с ускоре-нием. Это означает, что вдоль трубки тока изменяется давление жидкости. Получим связь между скоростью жидкости и давлением с учетом влия-ния силы тяжести. Для этого снова рассмотрим тонкую трубку тока с двумя сечениями на высотах и. За времяпройдут объемы жидкости

.

Изменение за время энергии объема жидкости, заключенного в начальный момент междуи, равно разности энергий малых объемов

Это изменение равно работе сил давления

.

Приравнивая друг другу два последних выражения, получаем

.

В пределе при ,объемыстягиваются в точки, а трубка тока переходит в линию тока. Таком образом на заданной линии тока выполняетсяуравнение Бернулли

Течение вязкой жидкости.

П

ри движении слоев жидкости друг относительно друга между ними возникаютсилы вязкого трения. Они связаны с переходом молекул из одного слоя в другой и их взаимодействием. Рассмотрим опыт Ньютона, с помощью которого был получен закон для сил вязкости (рис. 4). В этом опыте тонкая пластина с площадью двигалась под действием силыпо поверхности жидкости с постоянной скоростью. Глубина жидкости в сосуде равна. Сила вязкости, действующая на пластину, равна по величине и противоположна внешней силе. На основании проведенных измерений Ньютон сформулировал следующий закон:

.

Коэффициент в этой формуле зависит только от свойств жидкости и называетсякоэффи-циентом вязкости. Его размерность в СИ , а в СГС - 1 Пуаз. В приближении идеальной жидкости мы полагаем .

Из опыта следует, что вблизи пластины скорость жидкости близка к . Она спадает с глубиной по линейному закону, обращаясь в нуль на дне сосуда. Если направить осьвверх, а начало координат поместить на дне сосуда, то распределение проекции скорости на осьможно представить в виде (рис. 4):

.

В общем случае, при изменении скорости потока вдоль направления , проекция на осьсилы вязкого трения, действующей между слоями с площадьюможет выражена как

.

З

нак “-“ показывает, что слой с большей скоростью тормозится слоем с меньшей скоростью.

В качестве примера использования закона вязкого трения Ньютона рассмотрим течение вязкой несжимаемой жидкости в цилиндрической трубе длины и радиуса. Из условия несжимаемости следует, что скорость жидкости не меняется в направлении движения. Однако, она может изменяться по радиусу трубы. Выделим мысленно тонкий цилиндрический объем жидкости радиусаи высоты, ось которого совпадает с осью трубы (рис. 5). На боковую поверхность выделенного цилиндра действует сила вязкого трения

,

а на его основания – сила разности давлений

.

При стационарном течении . Отсюда получаем

.

Последнее равенство вытекает из независимости от. Здесь,- давления на левом и правом концах трубы соответственно (). Производя интегрирование с учетом граничного условия, получим

.

Из этого выражения видно, что на оси трубы скорость достигает максимального значения

и спадает по квадратичному закону до нуля при удалении от оси. Введем еще одно важное понятие.

Расход жидкости – количество жидкости, протекающее за единицу времени через поперечное сечение трубы.

С помощью выражения для и суммирования потоков по тонким кольцевым сечениям радиусаи шириныприходим кформуле Пуазейля

.

ЛЕКЦИЯ 26

Ламинарное и турбулентное течения. Движение тел в жидкостях и газах.

Ламинарное течение – течение жидкости, в котором можно указать точное значение скорости в данной точке в данный момент времени (можно построить линии тока).

Турбулентное течение – течение жидкости, в котором скорость в данной точке изменяется со временем беспорядочным образом (нельзя построить линии тока).

Так же, как и в предыдущей лекции, будем считать, что все сказанное о свойствах жидкости относится и к газу.

Рейнольдс экспериментально установил, что переход от ламинарного течения к турбулент-ному определяется значением безразмерной величины

,

называемой числом Рейнольдса. Здесь ,- плотность и скорость жидкости соответст-венно,- характерный поперечный размер потока,- коэффициент вязкости жидкости. Существует некоторое критическое значение числа Рейнольдса. Притечение является ламинарным, а при- турбулентным.

Понятие числа Рейнольдса связано с так называемым методом подобия, играющем важную роль в гидродинамике. Оказывается, что совершенно различные по своим параметрам потоки, обладающие одинаковым числом Рейнольдса, не только имеют одинаковый тип течения, но обладают и другими одинаковыми свойствами. Это обстоятельство, например, позволяет по результатам обдува в аэродинамической трубе макета самолета малых размеров получать информацию о технических параметрах реального самолета.

Р

ассмотрим обтекание твердого тела потоком жидкости или газа. Вблизи поверхности тела взаимодействие его молекул с молекулами жидкости приводит к “прилипании” жидкости к поверхности твердого. Если характеризовать это явление более строго, то речь идет о существо-вании слоя вблизи поверхности, в котором скорость жидкости относительно тела изменяется от нуля до скорости основного потока (рис. 1). Он называетсяпограничным слоем, а ширина соответ-ствующей области его эффективной толщиной. К потоку вне пограничного слоя можно применить теорему Бернулли. Из распределения линий тока на рис. 1 видно, что и. Значити. По этой причине позади тела возникает сила разности давлений, закручивающая траектории частиц в верхней части пограничного слоя. Это приводит кявлению отрыва, при котором пограничный слой отрывается от задней части тела и в виде хаотических вихрей уносится потоком жидкости. Движение этих вихрей является турбулентным и область их локализации позади тела назы-вается турбулентным следом. Из-за большой скорости вихревого движения давление в этой области ниже давления перед телом, что приводит к добавочной силе сопротивления. Чем уже турбулентный след, тем меньше эта сила. Поэтому быстро движущимся в жидкостях и газах телам придают обтекаемую форму.

Движение тел в жидкостях и газах.

Рассмотрим равномерное движение шара радиуса в жидкости со скоростью. Применим метод подобия и связанный с нимметод размерностей. Он состоит в следующем. Из пара-метров нужно составить величину размерности силы, зависящую от числа Рей-нольдса. Ее можно представить в виде

.

Для нахождения конкретного вида функции необходимо использовать дополнитель-ную информацию. Из опыта известно, что при малых скоростях. Это дает

, .

Более точный расчет дает значение (формула Стокса). Теперь мы можем строго определить, что понимается в этом случае под малой скоростью. Ее можно считать малой, если .

При можно пренебречь вязкостьюи зависимостью от числа Рейнольдса. Тогда выражение для силы сопротивления принимает вид

.

Эксперимент показывает, что при больших скоростях движения тел в жидкостях и газах такая зависимость действительно имеет место.

Силы, действующие на крыло самолета.

При обтекании крыла потоком воздуха давление над крылом меньше, чем под ним. В результате возникает подъемная сила крыла самолета (рис. 2). Турбулентный след позади крыла приводит к силе лобового сопротивления. Сумма этих сил создает равнодействующую силу. Уголмежду плоскостью крыла и горизонтом называетсяуглом атаки. Сначала, при увеличении угла атаки давление под крылом понижается и подъемная сила возрастает. При достижении критического угла атаки подъемная сила начинает падать. При этом в завихрен-ном пространстве над крылом давление ниже, чем в набегающем потоке, но выше, чем в случае полного обтекания крыла.

Жуковским и Чаплыгиным была построена теория обтекания крыла самолета на основе модели идеальной жидкости, в которой силы вязкости влияют лишь на создание кругового движения воздуха вокруг крыла. Такое движение было названо циркуляцией.

Рассмотрим важный частный случай.

Обтекание вращающегося цилиндра.

П

усть вращающийся вокруг собственной оси цилиндр обтекается потоком жидкости (или газа). Слои жидкости вблизи его поверхности вращаются вместе с ним. Для выбранных направлений движения на рис. 3 суммарная скорость потока сверху больше соответствую-щей скорости снизу. Тогда разность давлений создает подъемную силу, действующую на цилиндр снизу вверх. Это явление называетсяэффектом Магнуса. На нем основаны “крученые” удары футболистов и теннисистов.

Теория Жуковского и Чаплыгина позволяет вычислить подъемную силу крыла самолета без учета сил вязкого трения. В ней сначала находится распределение скоростей вокруг крыла с учетом циркуляции воздуха подобно эффекту Магнуса. Затем по этому распределению с помощью уравнения Бернулли вычисляется подъемная сила. Циркуляция вокруг крыла действительно существует. Ее возникновение объясняется законом сохранения момента импульса (рис. 4). При отрыве вихря в задней части крыла образуется циркуляция вокруг крыла в противоположном направлении. Если считать, что до отрыва вихря полный момент импульса равнялся нулю, то должно выполняться равенство

.

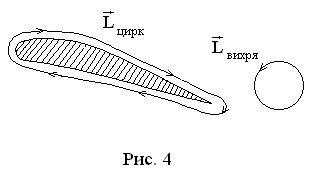
Процесс образования вихрей и возникновения циркуляции периодически повторяется. В результате создается постоянно действующая подъемная сила крыла самолета.