Явление застоя

Такое явление возникает, если на тело действует упругая сила, пропорциональная смеще-нию. При условии тело может занять любое положение. Оно практически никогда не остановится в среднем положении, определяемом условием. Явление застоя может приводить к неправильным показаниям измерительных приборов, содержащих удерживающие пружины.

Явление заноса

Пусть некоторое тело покоится на наклонной плоскости с углом наклона . В этом случае. Если заставить тело скользить поперек наклонной плоскости, оно начнет соскальзывать вниз, так как в этом случае исчезнет сила трения покоя, а сила трения скольжения в начальный момент будет направлена против скорости. Исчезновение силы трения покоя в направлении, перпендикулярном скорости, называется явлением заноса. Оно проявляется при резком торможении автомобиля, когда исчезает сила трения покоя в попе-речном направлении и автомобиль “заносит”.

1) Трение качения

Если тело цилиндрической или сферической формы без скольжения катится по твердой поверхности, то появляется другой тип силы трения – трение качения. Причина ее возникно-вения связана с пластической деформацией поверхности и соответствующим наклоном силы

, действующей на тело. Ее можно разложить на горизонтальную составляющую и вертикальную составляющую(рис. 1). Из опытных данных следует закон

,

где - коэффициент трения качения,- радиус тела. Для одинаковых материалов, то есть.

Это свойство используется в подшипниках для уменьшения трения во вращающихся деталях машин.

2. Вязкое (внутреннее) трение.

Этот вид трения обусловлен взаимодействием молекул жидкости или газа при движении в них тела. При малых скоростях движения из опыта следует закон

.

Коэффициент вязкого трения зависит от свойств тела и той среды, в которой оно движется.При больших скоростях зависимость от скорости становится квадратичной

.

Что понимается в этих законах под малыми и большими скоростями мы обсудим в дальней-шем при рассмотрении явлений гидродинамики.

В качестве примера движения тела при наличии вязкого трения рассмотрим задачу о движении тела в вязкой среде под действием постоянной силы . Второй закон Ньютона в проекции на направление действия силы имеет вид:

.

О

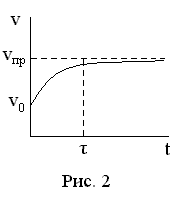
чевидно, силаможет ускорять тело лишь до пре-дельной скорости. Разделяя переменные и проводя интегрирование, получаем зависимость скорости тела от времени

,

где - начальная скорость тела,- характерное время достижения скорости.

ЛЕКЦИЯ 11

Гармонические колебания. Физический маятник.

Периодическое движение – через равные промежутки времени (период ) движение повторяется.

Гармоническое колебание материальной точки – координата точки изменяется по гармони-ческому закону

.

Здесь - амплитуда колебания, - круговая (циклическая) частота, , - частота, - фаза колебания, - начальная фаза.

Скорость материальной точки, совершающей гармоническое колебание:

.

Исходя из этого выражения, можно говорить, что при гармоническом колебании скорость опережает по фазе координату на .

Ускорение колебательного движения:

.

Таким образом, мы приходим к уравнению осциллятора

, (1)

составляющему основу теории колебаний (производная обозначена точками).

Собственные колебания возникают за счет собственных сил, существующих в самой системе. Частота таких колебаний называется собственной частотой.

Пример. Пружинный маятник.

, . Значит собственная частота , .

Полная энергия материальной точки при гармонических колебаниях:

.

Средние за период значения кинетической и потенциальной энергии:

, .

Таким образом, при гармонических колебаниях

(частный случай общей теоремы вириала).

Математический маятник – тело, подвешенное на невесомой нерастяжимой нити, размер которого намного меньше длины нити.

Физический маятник – тело, закрепленное на оси, расположенной выше центра масс.

Основной закон вращательного движения для такого тела

(). Преобразуем его к виду (1)

.

Тогда ,-период колебаний физического маятника.

Если размеры тела малы по сравнению с расстоянием (материаль-ная точка), тои мы приходим к известной формуле дляпериода математического маятника

.

Приведенная длина физического маятника – это длина математического маятника с тем же периодом колебаний, что и у физического. Приравнивая выражения для периодов, получим

.

Обозначим через точку, лежащую на продолжении отрезкаи отстоящую от точки подвеса на расстоянии. Точканазываетсяцентром качаний физического маятника. Можно показать, что физический маятник обладает следующим важным свойством: если физический маятник подвесить за центр качаний, то период его колебаний не изменится.

ЛЕКЦИЯ 12

Затухающие и вынужденные колебания. Резонанс.

В любой колебательной системе со временем происходит затухание колебаний, обусловлен-ное потерей энергии под действием неконсервативных сил. Рассмотрим затухание колеба-ний материальной точки под действием силы вязкого трения (лекция 10)

.

В этом случае 2-ой закон Ньютона для материальной точки под действием возвращающей сил и силы трения в проекции на ось можно представить в виде

. (1)

Коэффициент необязательно должен иметь смысл коэффициента жесткости. Он может описывать возвращающую силу любой природы.

Можно показать, что при условии решение уравнения (1) имеет вид

,

где - начальная амплитуда колебаний,-коэффициент затухания, - частота затухающих колебаний,- собственная частота.

Функция представляет собой амплитуду затухающих колебаний (рис. 1). Для характеристики скорости затухания колебаний вводитсялогарифмический декремент затухания

.

Затухающие колебания существуют при выполнении условия . Приимеет местоапериодический процесс, при котором точка возвращается в положение равновесия, не совершив ни одного колебания.