Калиничев в.Н., Безбах т.В.
Сборник задач и контрольных заданий по
инженерно-геологической графике
Москва
Издательство Российского университета дружбы народов
2009
ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ
Точка
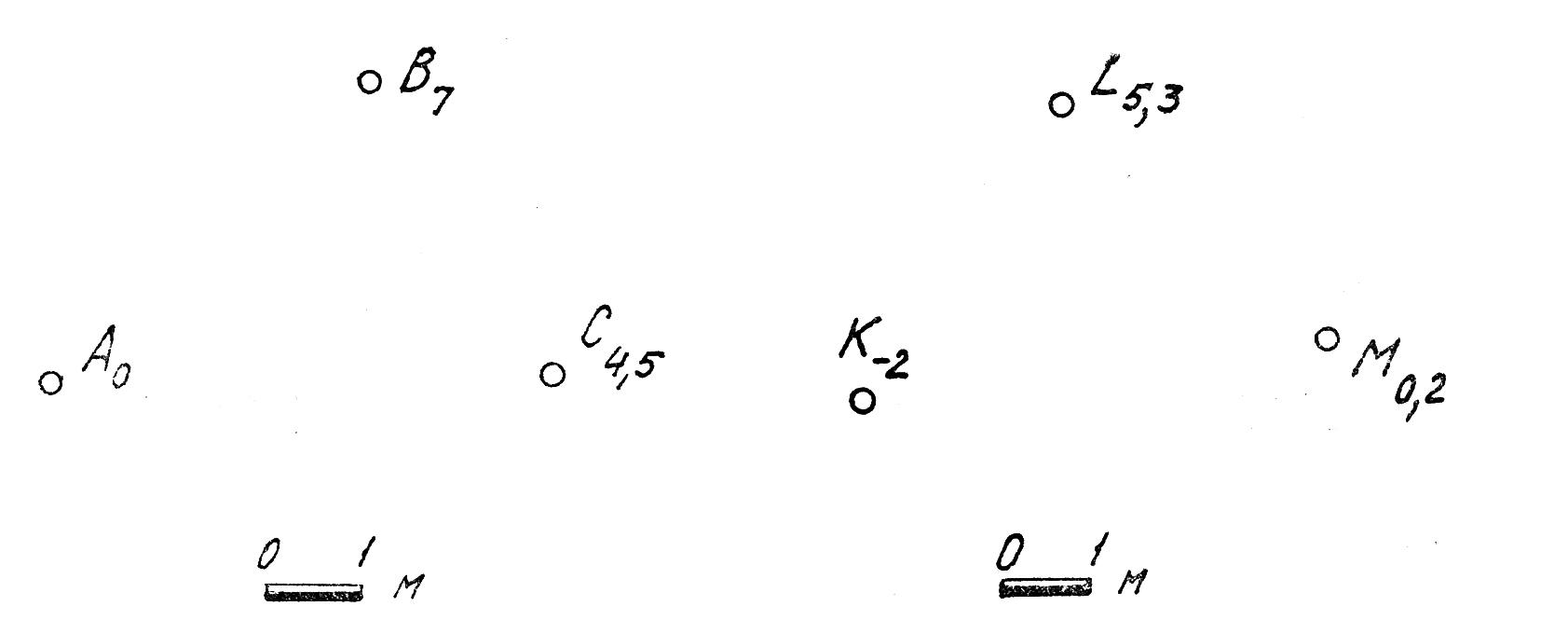
1. Определить отметки точек K, L и M, если плоскость проекций П0 будет смещена вниз на расстояние 2м.
Прямая линия
2. Определить азимуты падения прямых m(А5В1), n(C10D5), t(Es 300).
3
.
Определите азимуты простирания
горизонтальных прямых n(A5B5)
и h-3
Через точку В провести прямую t, азимут которой был бы равен 203°, а угол падения 230.
5. Через точку С провести горизонтальную прямую, азимут простирания которой был бы равен 127°.
6. Через точку D провести горизонтальную прямую, азимут простирания которой был бы равен 83°.
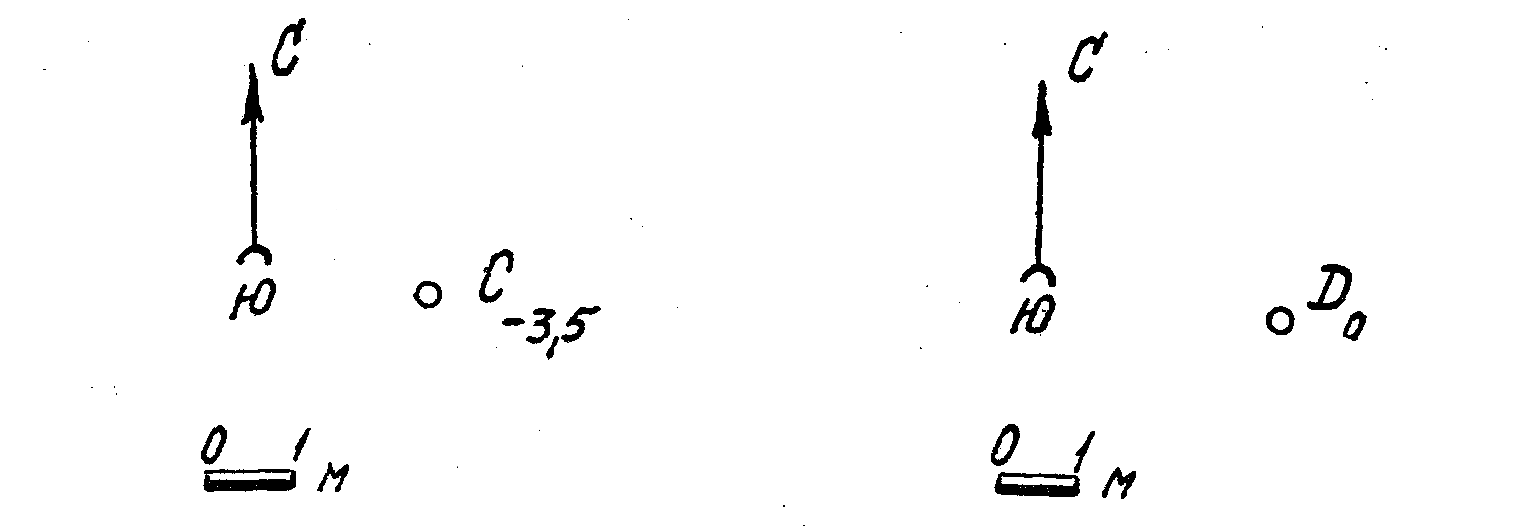
7. Определить истинную длину отрезка CD (C8,5D-4,25). Найти на прямой точку F с числовой отметкой 5.
8. На прямой п найти точку D, удаленную от точки F на расстояние 8,75 м.
9. Определить элементы залегания прямой l(M8N0).
10. Построить проекцию точки R, принадлежащей прямой m (C6,75 30°), отметка которой была бы равна 3,5 м. Решить задачу с помощью построения профиля и масштаба заложений.
11. Определить истинное расстояние от точки В до прямой h
12. Через точку R провести произвольную прямую, которая скрещивалась бы с прямой т под углом 90°. Определить истинное расстояние между конкурирующими точками прямых.
13.
Определить истинное расстояние от точек
В и А до прямой m(F13
350).
Плоскость
Определить элементы залегания плоскости Ω(t×l).
15. Определить элементы залегания плоскости Т(В13 т)
16.Изобразить плоскость Σ(В11 аз. пад. 245° 30°) горизонталями; высота сечения 1 м.
17. Через прямую п провести плоскость Λ, угол падения которой был бы равен 62°. Определить азимут линии падения плоскости.
18. Определить элементы залегания плоскости Σ исходя из условия, что наклонные прямые т, п и l, проходящие через точку А, пересекают эту плоскость в точках В, С и D на горизонтах 100, 150 и 70 м.
Взаимное расположение двух плоскостей
19. Через точку С провести плоскость Ф, которая была бы параллельна плоскости v(а×b).
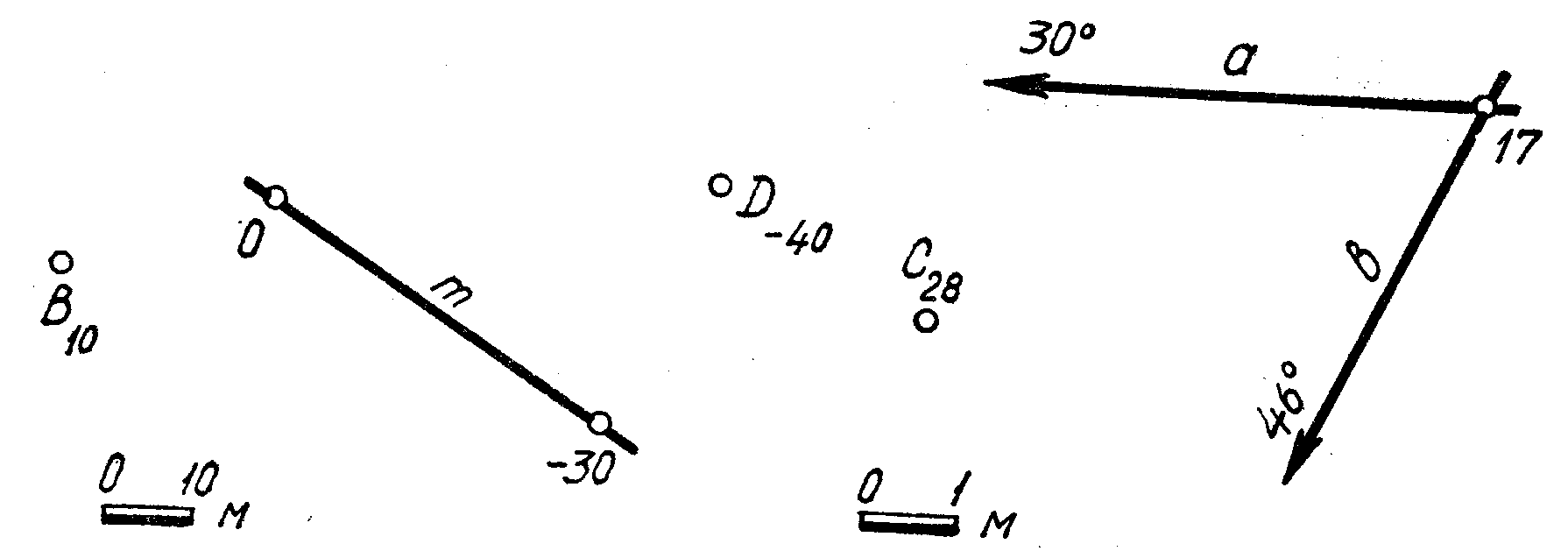
Через точку В провести плоскость ∑, которая была бы параллельна плоскости Ф(A10 m).
21. Построить линию т пересечения плоскости Σ с плоскостью Λ.
22. Построить линию b пересечения плоскости Т с плоскостью Р.
23.
Построить линию а
пересечения
плоскости Θ(т×п)
с
плоскостью
Δ(В8аз. простир. l50° 90°).
24. Построить линию t пересечения плоскости Ω с плоскостью Σ, проходящей через прямую m(А12 300) перпендикулярно к плоскости Σ.
25. Определить истинное расстояние между параллельными плоскостями Т(m×n) и Ω(t×l).
26. Через точку А провести прямую b, которая пересекла бы скрещивающиеся прямые т и п.
Взаимное расположение прямой и плоскости
27. В каком направлении надо пересечь плоскость Ψ(m×h) вертикальной плоскостью Θ, чтобы в сечении получить прямую t, угол падения которой был бы равен 15°.
28. Через точку Т провести прямую l, которая была бы параллельна плоскости Ω(a×b) и имела бы угол падения, равный 15°
29. Через точку F провести плоскость Δ, которая была бы параллельна прямой t(R17, 250) и имела бы угол падения равный 57°.
30. Определить элементы залегания плоскости К, которая проходит через точку А параллельно скрещивающимся прямым l и t.
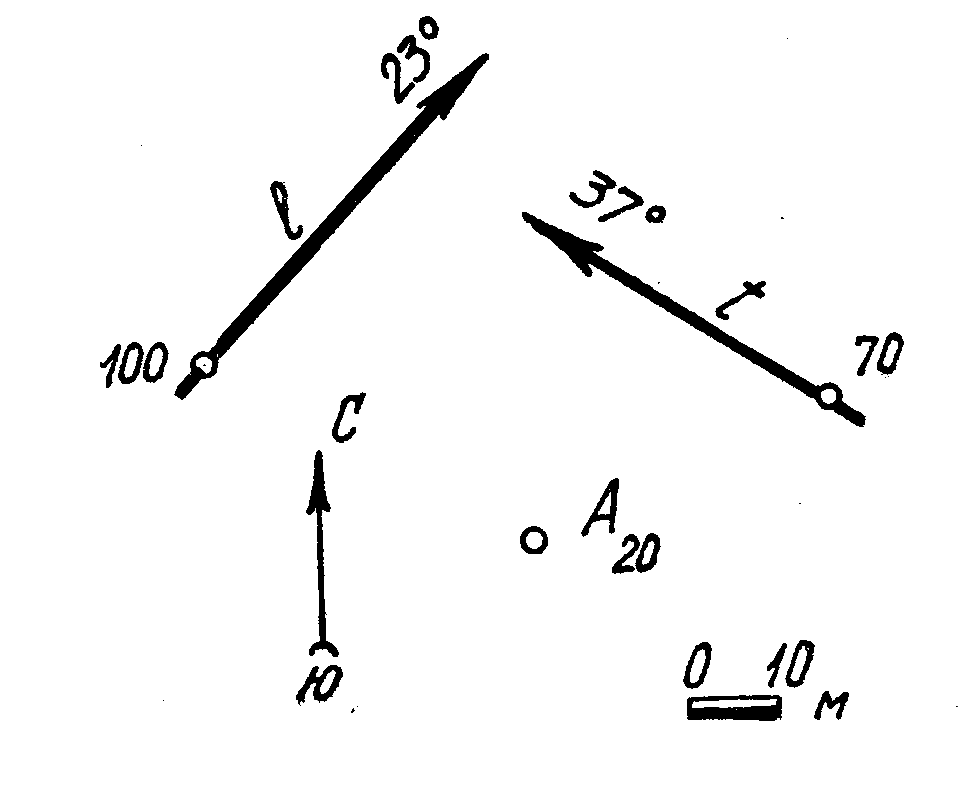
31. Через точку А провести прямую т, которая была бы параллельна плоскости Σ и пересекала бы прямую t.
32. Провести произвольную прямую b, которая была бы параллельна плоскости Ω и пересекала бы прямые cиd
33. Построить точку D пересечения прямой т(А12 380) с плоскостью Ψ(a×b). Определить видимость прямой относительно плоскости.
34. Прямая t(F40 35°) пересекает параллельные плоскости Ω(F25 аз. пад. 260° 40°) и Т в точках Р и L, отстоящих друг от друга на расстоянии 10 м. Определить истинное расстояние между плоскостями Ω и Т.
35. Провести произвольную прямую l, которая пересекла бы три скрещивающиеся прямые а, b и с.
36. Определить истинное расстояние от точки R до плоскости Σ.
37. В плоскости Σ построить геометрическое место точек, равноудаленных от точек А и В.
38. Построить прямую d, которая была бы перпендикулярна к плоскости Т и пересекла бы скрещивающиеся прямые r и f.
