2.7. Случайные сигналы

В отличие от детерминированных сигналов, форма которых известна точно, мгновенные значения случайных сигналов не известны и могут быть предсказаны лишь с некоторой вероятностью. Характеристики таких сигналов являются статистическими.

В таком вероятностном описании нуждаются следующие два основных класса сигналов.

1. Шумы – хаотические изменяющиеся во времени сигналы, возникающие в различных физических системах из-за беспорядочного движения носителей.

2. Сигналы, несущие информацию, поскольку её смысл изначально неизвестен.

Математическая модель изменяющегося во времени случайного сигнала называется случайным процессом.

До регистрации (или приёма) случайный сигнал следует рассматривать как случайный процесс, представляющий собой множество или ансамбль функции , которые обладают некоторой статистической закономерностью.

Одна из таких функций, ставшая полностью известной после приёма сообщения, называется реализацией случайного процесса, она является уже не случайной, а детерминированной.

2.7.1.Модели случайных процессов

Для анализа свойств случайного процесса необходимо задать математическую модель такого процесса.

Рассмотрим примеры

1. Гармонический сигнал со случайной начальной фазой

–амплитуда – известна, т.е. детерминирована

–частота детерминирована

–случайная начальная фаза, принимающая любое значение на интервале .

При равномерном распределении такой начальной фазы на интервале плотность вероятности:

2. Случайный телеграфный сигнал

Возможны значения , переключение из одного состояния в другое происходит в случайные моменты времени.

Функция распределения вероятности, т.е. вероятности того, что за время произойдётпереключений (случайная величина!) имеет вид:

,

где – параметр, определяющий среднюю частоту переключений.

Это выражение описывает закон Пуассона.

2.7.2. Вероятностные характеристики случайного процесса Функциональные характеристики.

Функция распределения вероятности (cumulative distribution function CDF)

(3.1)

Определить вероятность того, что в момент времени значение случайного процессане превосходит

а) CDF является неубывающей функцией;

б) вероятность попадания значения случайного процесса в интервал :

(3.2)

Одномерная плотность вероятности (probability density function, PDF)

(3.3)

Т.е. является производной от функции распределения и определяет характер скорость её изменения:

а) плотность вероятности является неотрицательной функцией

б) вероятность попадания в произвольный интервал:

(3.4)

Очевидно, что:

Числовые характеристики

Математическое ожидание (mean value) – это теоретическая оценка среднего взвешенного значения случайного процесса в момент времени :

(3.5)

Дисперсия (variance) – характеризует среднюю мощность отклонений случайного процесса от его среднего

(3.6)

Среднеквадратическое отклонение (standard deviation):

(3.7)

Примеры случайных процессов с различными законами распределения

1. Равномерное распределение: для такой случайной величины плотность вероятности является постоянной, т.е.

Функция распределения вероятности такой случайной величины на интервале линейно возрастает от 0 до 1:

Математическое ожидание:

;

Дисперсия: согласно (3.6) с учётом математического ожидания получаем:

СКО: .

2. Нормативный закон распределения – достаточно часто встречается на практике, например, он характерен для помех канала связи: при этом одномерная плотность вероятности нормальной случайной величины определяется как:

,

где и– соответственно мат ожидание и дисперсия процесса (случайные величины).

График плотности вероятности в этом случае имеет вид (дляи):

Функция распределения вероятности в этом случае обычно выражается через интеграл вероятности:

В зарубежной литературе часто используется функция ошибок (error function):

между исуществует взаимосвязь:

С учётом этого функция распределения для нормального закона с математическим ожиданием и дисперсией:

.

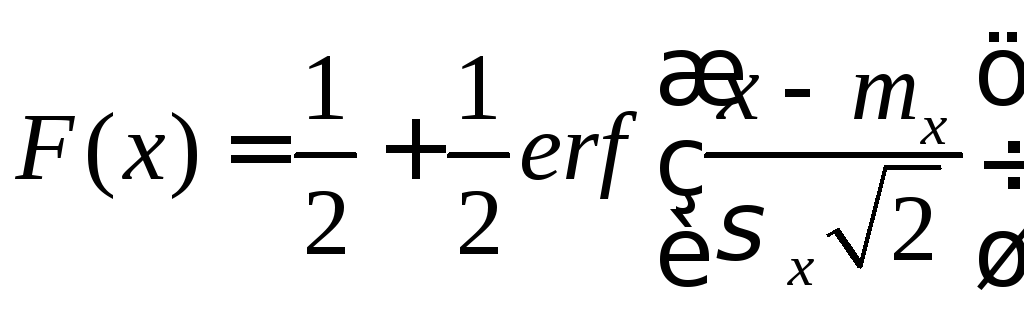Важное свойство:

При суммировании достаточно большого числа равномощных статистических независимых случайных величин с произвольными плотностями распределения вероятности, плотность распределения вероятности суммы стремиться к нормальной. Это положение носит название центральной предельной теоремы.

Кроме того, для математического анализа случайных величин полезным является то, что из некоррелированности гауссовых случайных величин следует их статистическая независимость.