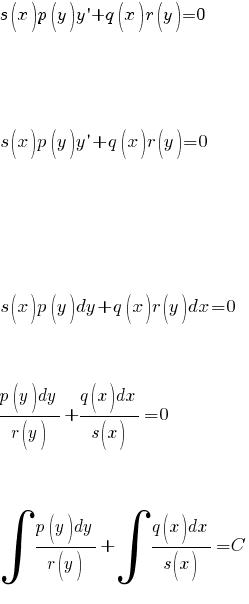
18. Дифференциальные уравнения с разделяющимися переменными

Дифференциальные уравнения с разделяющимися переменными – это уравнения вида

Решение дифференциальных уравнений с разделяющимися переменными

В исходном уравнении:

(1)

Выразим y' через дифференциалы:

;

;

Умножим на dx:

;

Иногда уравнение задается в таком виде. Это означает, что переменные x и y равноправны. Разделим уравнение на s(x)r(y):

Интегрируем:

(2)

Поскольку мы делили на s(x)r(y), то получили интеграл уравнения при s(x)≠ 0 и r(y)≠ 0. Далее следует рассмотреть решения, определяемые уравнениями s(x)= 0 и r(y)= 0, которые могут давать несколько значений типа x = const, y = const, также удовлетворяющие исходному уравнению (1). Часть этих решений может уже содержаться в решении (2).

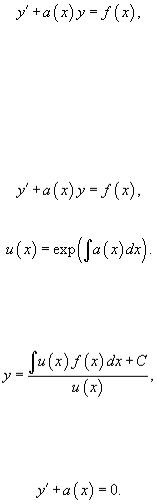
19. Линейные дифференциальные уравнения первого порядка

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:

•Использование интегрирующего множителя;

•Метод вариации постоянной.

Использование интегрирующего множителя

Если линейное дифференциальное уравнение записано в стандартной форме:

то интегрирующий множитель определяется формулой:

Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x).

Общее решение диффференциального уравнения выражается в виде:

где C − произвольная постоянная.

Метод вариации постоянной

Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:

Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x).

Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.

Задача Коши

Если, кроме дифференциального уравнения, задано также начальное условие в форме y(x0) = y0, то такая задача называется задачей Коши.

Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y(x0) = y0.

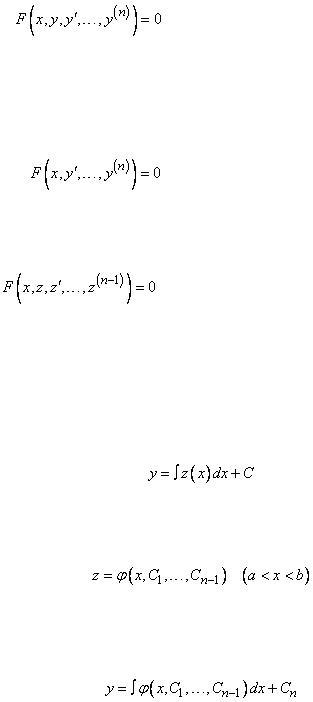
20. Понижение порядка

Во многих случаях удается свести дифференциальное уравнение -го порядка

(1)

к дифференциальному уравнению более низкого порядка, путем введения новой неизвестной функции. Рассмотрим некоторые типы уравнений, допускающих понижение порядка.

I. Пусть левая часть уравнения (1) не содержит явно искомую функцию , т. е. уравнение имеет вид

Введем новую функцию , тогда и уравнение (2) перепишется так:

т. е. относительно функции оно представляет собой уравнение -го порядка.

Любое решение , этого уравнения мы должны подставить в дифференциальное уравнение и решить последнее относительно :

.

Появилась произвольная постоянная. Часто некоторые решения дифференциального уравнения (3), не обязательно все, образуют семейство функций

,

зависящих от параметров . Ему соответствует семейство решений дифференциального уравнения (2)

,

зависящих от параметров .

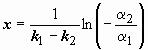
21. Линейная зависимость/независимость сложных функций. Определитель Вронского.

Система функций y1(x), y2(x), …, yn(x) называется линейно зависимой на интервале (a, b), если

существует набор постоянных коэффициентов 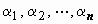, не равных нулю одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a, b):

для .

Если равенство для возможно только при

, система функций y1(x), y2(x), …, yn(x) называется линейно независимой на интервале (a, b).

Другими словами, функции y1(x), y2(x), …, yn(x) линейно зависимы на интервале (a, b), если существует равная нулю на (a, b) их нетривиальная линейная комбинация. Функции y1(x), y2(x), …, yn(x) линейно независимы на интервале (a, b), если только тривиальная их линейная комбинация тождественно равна нулю на (a, b).

Примеры: 1. Функции 1, x, x2, x3 линейно независимы на любом интервале (a, b). Их линейная комбинация - многочлен степени - не может иметь на (a, b) больше трёх корней, поэтому равенство = 0 для возможно только при

.

Пример 1 легко обобщается на систему функций 1, x, x2, x3 , …, xn. Их линейная комбинация - многочлен степени - не может иметь на (a, b) больше n корней.

3. Функции линейно независимы на любом интервале (a, b), если .

Действительно, если, например, , то равенство 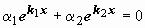имеет место в единственной

точке .

4. Система функций также линейно независима, если числа ki (i = 1, 2, …, n) попарно различны, однако прямое доказательство этого факта достаточно громоздко.

Как показывают приведённые примеры, в некоторых случаях линейная зависимость или независимость функций доказывается просто, в других случаях это доказательство сложнее. Поэтому необходим простой универсальный инструмент, дающий ответ на вопрос о линейной зависимости функций. Такой инструмент - определитель Вронского.

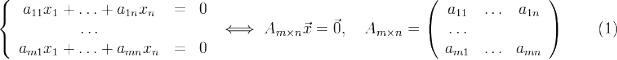
22. Фундаментальная система решений дифференциального уравнения.

Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.

Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

23. Линейные неоднородные уравнения с постоянными коэффициентами. (Теорема о сумме общего и частного решений.)

Метод вариации постоянных

Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.

Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x).

Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:

Метод неопределенных коэффициентов

Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.

Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1.

2.где Pn(x) и Qm(x) − многочлены степени n и m, соответственно.

Вобоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.

Вслучае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении.

Вслучае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.

Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Принцип суперпозиции

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида

то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

С1ф1+С2ф2=0 | u1ф1+u2ф2=0 (где u – функция)

С1ф1’+С2ф2’=[] | u1ф1’+u2ф2’=[]

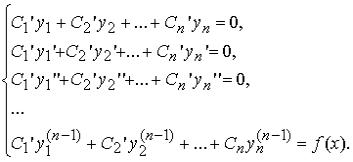
24. Метод Лагранжа. Вариация произвольных постоянных

Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения частного решения.

Рассмотрим линейное неоднородное дифференциальное уравнение

y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x).

с непрерывными на [a; b] коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y1(x), y2(x),..., yn(x) решений соответствующего однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) ,

где C1(x), C2(x) , ... , Cn(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Справедливо следующее утверждение.

Пусть y1(x), y2(x),..., yn(x) — фундаментальная система решений однородного уравнения y(n) + an-1(x)y(n - 1) +

... + a1(x)y' + a0(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) непрерывна на [a; b], то его частное

решение можно искать в виде

y*(x) = y(x,C1,..., Cn) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) .

Неизвестные функции C1(x), C2(x) , ... , Cn(x) находятся из системы

25. Связь дифференциального уравнения с системой уравнений

Дифференциальные уравнения высших порядков и системы дифференциальных уравнений. Д. у. n-го

порядка с одной неизвестной функцией у (х) независимого переменного х записывают так:

F (х, у, y', у", ..., y(n-1), y(n)) = 0. (1)

Если ввести дополнительные неизвестные функции

y1 = y', y2 = y", ..., yn-1 = y (n-1), (2)

то уравнение (1) можно заменить системой из n уравнений с n неизвестными функциями, но зато 1-го порядка. Для этого достаточно к n - 1 уравнениям (2) присоединить уравнение

F (x, у, y1, у2, ..., yn-1, y'n-1) = 0.

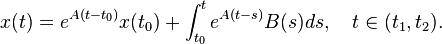
26.Система дифференциальных уравнений с постоянными коэффициентами.

Вслучае , матрцант равен

,

где — матричная экспонента, следовательно, матрица Коши:

,

,

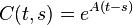таким образом, в этом случае для получения матрицы Коши достаточно подставить (t - s) в качестве аргумента матрицанта.

Общее решение системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами имеет вид:

где C = (C1, C2, ..., Cn) T − произвольный n-мерный вектор. Символ T обозначает операцию транспонирования. В этой формуле мы не можем записать вектор C перед матричной экспонентой,

поскольку произведение матриц не определено.

Для задачи с начальными условиями (задачи Коши) компоненты вектора C выражаются через начальные условия. В этом случае решение однородной системы записывается в виде

Таким образом, решение однородной системы уравнений становится известным, если вычислена соответствующая матричная экспонента. Для ее вычисления можно воспользоваться бесконечным рядом, который содержится в определении матричной экспоненты. Однако часто это позволяет найти матричную экспоненту лишь приближенно. Для решения задачи можно использовать также алгебраический способ, основанный на последнем свойстве из перечисленных выше. Рассмотрим этот способ и общий ход решения более подробно.

Алгоритм решения системы уравнений методом матричной экспоненты

1.Сначала находим собственные значения λi матрицы (линейного оператора) A;

2.Вычисляем собственные и (в случае кратных собственных значений) присоединенные векторы;

3.Из полученных собственных и присоединенных векторов составляем невырожденную матрицу линейного преобразования H. Вычисляем соответствующую обратную матрицу H −1;

4.Находим нормальную жорданову форму J для заданной матрицы A, используя формулу

Примечание: В процессе нахождения собственных и присоединенных векторов часто становится ясной структура каждой жордановой клетки. Это позволяет сразу записать жорданову форму без вычисления по указанной формуле.

5.Зная жорданову форму J, cоставляем матрицу exp (tJ). Соответствующие формулы для такого преобразования выводятся из определения матричной экспоненты. Для некоторых простых жордановых форм матрица exp (tJ) имеет вид, приведенный в таблице:

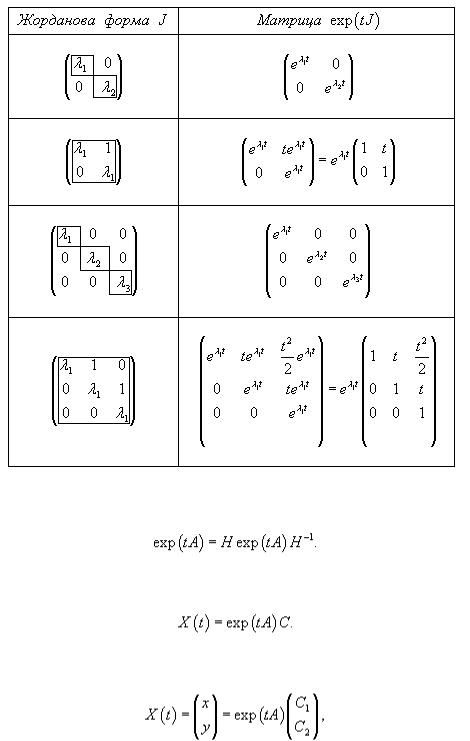
6.Вычисляем матричную экспоненту exp (tA) по формуле

7.Записываем общее решение системы, которое имеет следующий вид:

В случае систем дифференциальных уравнений 2-го порядка общее решение выражается формулой

где C1, C2 − произвольные постоянные.