Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Типовик матан 5 модуль

.pdf

Скачиваний:

184

Добавлен:

14.04.2015

Размер:

1.22 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

движении от точки L к точке M координата z меняется от 0 до 1. Следовательно,

ILM = −∫(4 −4z −2z −2)dz =

=1.

= 2∫(3z −1)dz =2

− z

−1

в) Отрезок MK представляет собой отрезок прямой, заданной

y = 0

, откуда

следует,

что

dy = 0

. При

системой

x = 2 −2z

dx = −2dz

движении от точки M к точке

K координата

z меняется от 1 до 0.

Следовательно,

((2 −2z)(−4) −(2 −2z −2z −2))dz =

IMK = ∫

0
= ∫(12z−8)dz =(6z2 −8z)		10 = −6 +8 = 2 .
= ∫(12z−8)dz =(6z2 −8z)		10 = −6 +8 = 2 .
1

Окончательно получим C = – 8 + 1 + 2 = – 5.

II способ. Найдем циркуляцию векторного поля по той же замкнутой линии с помощью теоремы Стокса, согласно которой циркуляция векторного поля по контуру равна потоку ротора

векторного	поля	через	поверхность,		ограниченную контуром
G	G	Выразим	поток	ротора		через поверхностный
C = ∫∫rota ndS .
S
интеграл второго рода			G		G	G
	G	G
C = ∫∫rota		ndS = ∫∫	(rota)x dydz +		(rota)y dxdz +(rota)z dxdy .
	S	S		(rotaG)z
В этой формуле (rotaG)x , (rotaG)y ,						– составляющие ротора

по осям координат Ox, Oy, Oz соответственно. Сторона поверхности выбирается таким образом, чтобы при наблюдении с конца нормали обход контура происходил так, чтобы поверхность оставалась слева

(рис. 7).

Поверхностный интеграл второго рода выразим через сумму двойных интегралов, каждый из которых берется по проекции поверхности S на координатные плоскости Dyz, Dxz, Dxy:

C = ±∫∫rotaGxdydz ±∫∫rotaGy dxdz ± ∫∫rotaGz dxdy .

Dyz

Dxz

Dxy

Перед каждым интегралом выбирается знак «+», если нормаль образует острый угол с осью координат, перпендикулярной к плоскости, на которую проецируется поверхность; в противном

случае выбирается знак « – ».

Найдем ротор векторного поля в нашей задаче:

∂

rota =

∂x

∂y

∂z

∂x

∂y

∂z

2x +2 y 0 −x −2 y +2z +2

=∂∂y (−x −2 y +2z +2) − ∂∂z 0 iG− ∂∂x (−x −2 y +2z +2) − ∂∂z (2x +2 y) Gj +

+∂∂x 0 − ∂∂y (2x +2 y) kG = −2iG+ Gj −2kG.

Циркуляция равна C = ∫∫(−2)dydz +dxdz +(−2)dxdy . В нашем

случае нормаль к поверхности образует острые углы с осями координат. Поэтому, перейдя от поверхностного интеграла второго рода к двойным интегралам, получим

C = ∫∫	(−2)dydz + ∫∫		dxdz + ∫∫ (−2)dxdy =
OLM		OKM	OKL
= −2 ∫∫	dydz + ∫∫	dxdz −2 ∫∫ dxdy = −2S OLM + S OKM −2S OKL ,
OLM	OKM		OKL
где S OLM , S OKM , S OKL		– площади соответствующих треугольников

(рис. 7). Применив формулу площади прямоугольного треугольника

S = 12 ab , где a и b катеты, окончательно получим C = −2 +1−4 = −5.

Ответ: C = – 5.

Задача 9. Дано векторное поле aG(M ) = −3x2i + 2 yzjG + ( y2 − 2z)k

1)Проверьте, является ли векторное поле соленоидальным или потенциальным.

2)Если поле потенциально, найдите его потенциал.

Решение. 1) Условием соленоидальности векторного поля является равенство его дивергенции нулю во всей области его определения. Данное векторное поле определено при любых значениях переменных. Для проверки его соленоидальности найдем дивергенцию векторного поля.

∂(−3x2 )

∂(2xy)

∂( y2 −2z)

diva(M ) =

∂x

∂y

∂z

= −6x +2z −2

Дивергенция обращается в ноль не при всех значениях x, y, z, а

лишь при условии – 6x + 2z – 2 = 0, т. е. на плоскости

z = 1+ 3x,

поэтому поле не соленоидально.

Условием потенциальности векторного поля является равенство

его ротора нулевому вектору во всей области определения поля. Для

проверки его потенциальности найдем ротор векторного поля.

∂

rota

∂x

∂y

∂z

−3x2

2 yz y2 −2z

∂( y2 −2z)

∂(2 yz) G

∂(−3x2 )

∂( y2 −

2z)

∂(2 yz)

∂(−3x2 ) G

∂y

−

∂z

−

∂x

−

∂y

= (2 y − 2 y)i + 0 Gj + 0k = 0

Таким образом,

rotaG(M ) = 0 при любых значениях переменных.

Значит, поле потенциально.

2) Поскольку поле потенциально, оно является градиентом

некоторого скалярного

поля

U(M), т. е.

a(M ) = gradU (M ) .

Скалярное поле U(M)

называется потенциалом

векторного

поля

aG(M ) . Его

полный

дифференциал

задается выражением

dU = axdx + aydy + azdz , в котором ax, ay, az – координаты векторного поля aG(M ) . Задача нахождения потенциала сводится к нахождению

функции трех переменных по ее полному дифференциалу. Для этого следует найти криволинейный интеграл второго рода, не зависящий от пути интегрирования

M M

U (M ) = ∫ dU +C = ∫ axdx + aydy + azdz +C ,

M0 M0

где M0 = M0(x0, y0, z0) – начальная точка, M = M(x, y, z) – конечная точка пути интегрирования.

Обозначим переменные интегрирования через x , y , z . В

качестве начальной точки выберем начало координат О(0; 0; 0), а в качестве конечной точки – текущую точку M(x, y, z). В нашем случае полный дифференциал имеет вид

dU = −3x2dx + 2 yzdy + ( y2 − 2z)dz .

Тогда потенциал U(M) = U(x, y, z) равен

( x; y;z)

U (x, y, z) = ∫ −3x2dx + 2 yzdy +( y2 −2z)dz +C

(0;0;0)

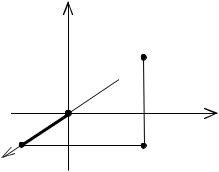
Вкачестве пути интегрирования выберем ломаную ОАВМ, где

О= О(0; 0; 0), А = А(x; 0;0), B = B(x; y; 0), M = M(x, y, z) (рис. 8).

Пользуясь свойством аддитивности криволинейного интеграла, представим его в виде суммы интегралов, найденных на каждом отрезке данной ломаной.

• Отрезок	ОА		задается	z
уравнениями	y = 0	,	откуда
	z = 0			M

следует, что dy = 0 . Переменная
x	dz = 0					O
x	меняется от 0 до x. Интеграл					y
по	отрезку	ОА		равен	A	B
по	отрезку	ОА		равен	x
	x		x		x
	x
IOA = ∫(−3x2 )dx = −x3				= −x3		Рис. 8

			0
	0

•Отрезок АВ задается уравнениями x = x = const , откуда следует,

z = 0

dx = 0

что . Переменная y меняется от 0 до y. Интеграл по отрезку

dz = 0

АB равен IAB = ∫0dy =0 .

•Отрезок ВM задается уравнениями x = x = const , откуда следует,

y = y = const

что dx = 0	. Переменная z меняется от 0 до z. Интеграл по отрезку
dy = 0
	z		z	= y2 z − z2 .
BM равен IBM = ∫( y2		−2z)dz =( y2 z − z2 )	z
BM равен IBM = ∫( y2		−2z)dz =( y2 z − z2 )	0
	0

Окончательно получим

U (x; y; z) = IOA + IAB + IBM +C = −x3 + y2 z − z2 +C

Ответ 1) Поле не соленоидально, поле потенциально. 2)U (x; y; z) = −x3 + y2 z − z2 +C .

Расчетные задания

I.Плоская область D ограничена заданными линиями.

1)Сделайте схематический рисунок области D.

2)С помощью двойного интеграла найдите площадь области D.

1.	y = 2 /(x2 +1), y = x, x = − y .	2.	y = 2x −6, x = 3 − y , y = log2 x .
3.	y = x3 , x + y = 2, y = 3x +2 при	4. y = x +1, x − y =1, x + y = −1.
x + y ≤ 2 .
5. y = 2x , x = − 2 y, x +2 y = 2 .		6.	y = x +2, x = 2 y , y = −x .

7. y = 0,5x , y − x =1, y + 4x = −4 .

8. x = y −1, x = 1− y, y = x2 −1.

9. x =

2 − y , y = − 2x, y = x .

10. y = 3 x, x = −

y +2, y =3x −2 .

11. y = −x3 , y − x = 2, x

3 =

2 − y

12. y − x =1, x + y = −1, x =

y +1 .

при y ≥ −x3 .

13.

y = 4x , y = (x −1)2 , x =

14. y =

−x, x =

y, y =

x2 +1

15.

x + y =1, y = 2x , 4x − y = 4 .

16.

y =

4 − x, x + y = −2,

x =

2 y −2 .

17.

y =

2 − x, x = −

2 y , y = x .

18.

x =

2 y , y = 0,5x , 2 y − x = 2 .

19. y = 3 x, x + y = 2, y

3 = − 2 − x

20.

x =

1− y, y − x =1, y + x = −1.

при y ≤ 3 x .


21.	y = log2 x, y =	x −1		, y = 2 .
			ln 2

23.	4 y − x = 4, y = log2 x, x + y =1.
25. y = log2 x, y =			2x, 2x + y = 2.

27.	x = y3, x =1 −		y +1, x + y = 2 .
29.	y = x, x + y = 2, x			y = 2 .

22.	y = 4 , y = 2x, y = 4x .
	x
24.	x = −	y , y = x, y = 2 − x .
26.	x = arcsin y, y =		π	, y =	8x
26.	x = arcsin y, y =			, y =	π
при x ≥ 0			2x		π
при x ≥ 0
28.	y = 2x ,	x + y = 3, x +3y =3 .
30.	y = 4−x , y = (x +1)2 , x = −					2	.
30.	y = 4−x , y = (x +1)2 , x = −						.
						y

II.Тело Т ограничено заданными поверхностями.

1)Сделайте схематический рисунок тела Т.

2)С помощью тройного интеграла найдите объем тела Т, перейдя к цилиндрическим или сферическим координатам.

1.		z = 2 +				4 − x2 − y2 , z =						x2 + y2 , x = 0 при x ≤ 0 .
2.		z + 4 = x2 + y2 , 9z = 5(x2 + y2 ), y = 0 при y ≥ 0 .
3.	3z2 = x2 + y2 , z2 = 3(x2 + y2 ), x2 + y2 + z2 = 9 при z ≥0 .
4.		x2 + y2 = z2 −5,						z2	=	x2 + y2			, x = 0 при z ≥0 , x ≥ 0 .
							9
		z2			x2 + y2							4
5.			=1−				, x2		+ y2			=9, z = 0, x = 0 при z ≥0 , x ≤ 0 .
	9
						25					x2 + y2
6.		z = 4 −2				x2 + y2 , z =								−2, y = 0 при y ≥ 0 .

			5								5	2
7.		z =		9		− x2 − y2 , z =						x2 + y2 , x = 0 при x ≤ 0 .
			3								4
8.		x2 + y2 + z2 = 4, x2 + y2 +(z −2)2 = 4 при 0 ≤ z ≤ 2 .
9.		z =		4 − x2 − y2 , z =							x2 + y2 −2, x = 0 при x ≥ 0 .

10.z = 4 − x2 − y2 , 9z = −5(x2 + y2 ), y = 0 при y ≤ 0 .

11.z = 2 − x2 + y2 , z = 4 − x2 − y2 , x = 0 при x ≤ 0 .

12.	z2 = 3(x2 + y2 ), x2 + y2 + z2 = 2z, x = 0 при x ≥ 0 ,
	0 ≤ z ≤ 3(x2 + y2 ) .
13.	x2 + y2 +4z2 = 4, x2 + y2 =1, x = 0, z = 0 при x2 + y2 ≥1,

x ≤ 0 .

14.2z = 4 − x2 − y2 , z = 2 x2 + y2 −4, y = 0 при y ≥ 0 , z ≥ −4 .

15.z = x2 + y2 , z +2 = x2 + y2 , x = 0 при x ≤ 0 .

16.	x2 + y2 + z2 =9, x2 + y2 + z2 = 2 3z, x =0, z =0 при x ≥ 0 ,
	0 ≤ 2 3z ≤ x2 + y2 + z2 .
17.	z = − 4 − x2 − y2 , z = 2 − x2 + y2 , y = 0 при y ≥ 0 , z ≤ 2 .

18.z = x2 + y2 , z = 95 (x2 + y2 ) +4, y = 0 при y ≤ 0 .

19.z = 2 − x2 − y2 , z = − x2 + y2 , x = 0 при x ≥ 0 .

20.	z2 = x2 + y2 , x2 + y2 + z2 = 4z, x = 0 при x ≤ 0 ,
	z ≥			x2 + y2 .
21.	4x2 +4 y2 + z2 = 36, x2 + y2 = 4, y = 0, z = 0 при
	y ≥ 0 , z ≤0 , x2 + y2 ≥ 4 .
22.	z = −2				x2 + y2 , 2(z +6) = x2 + y2 , y = 0 при y ≤ 0 .
23.	z =			x2 + y2 +9, 4z =5					x2 + y2 , y = 0 при y ≥ 0 .
24.	3z2 = x2 + y2 , z2 = 3(x2 + y2 ), x2 + y2 + z2 = 4z, x = 0 при
	x ≥ 0 , z ≥ 0 .
25.	z = 2 −					4 − x2 − y2 , z = 4 − x2 + y2 , y = 0 при y ≤ 0 .
26.	z = −			5		(x2 + y2 ), z = −			x2 + y2 +9, y = 0 при y ≤ 0 .
26.	z = −		16			(x2 + y2 ), z = −			x2 + y2 +9, y = 0 при y ≤ 0 .
			16
27.	x2 + y2 + z2 = 9, x2 + y2 + z2 −2 3z = 0 при x2 + y2 + z2 ≥ 9 .
28.	x2 + y2 + z2 = −2z, x2 + y2 + z2 =1 при x2 + y2 + z2 ≥1.
		x2 + y2						3(x2	+ y	2 )
29.	z =						+1, z =				−1, x = 0, y = 0 при
29.	z =		4				+1, z =		4		−1, x = 0, y = 0 при
			4						4

x ≥ 0, y ≥ 0 .

30.	z =3 −	3(x2	+ y2 )	, z =1−	x2	+ y2	, x = 0, y = 0	при
			4			4

x ≤ 0, y ≤ 0 .

III. С помощью криволинейного интеграла первого рода найдите массу M дуги плоской материальной кривой, заданной

уравнениями а) y = f(x) при	x1	≤ x ≤ x2	x
			; б)
			y

t1 ≤t ≤t2 , если плотность вещества равна ρ(x, y) .

=ϕ(t)

=ψ(t) при

1.а)

б)

2.а)

б)

3.а)

б)

4.а)

б)

5.а)

б)

6.а)

б)

y = x x, ρ(x, y)

=8, x

= 1

, x

5 ;

= e

cos t

ρ(x, y) =1, t1 = ln 2, t2 =ln 8 .

= et

sin t

= −1

, x = 1

y = arcsin x +

1 − x2 , ρ(x, y)

=1, x

;

x = et

, ρ(x, y) =3, t1 = ln 8, t2 = ln15 .

1,5t

y =

, ρ(x, y) =

, x

= 0, x =

;

1+2 y

= cos

ρ(x, y) =8, t1 =

, t2 =

=sin3 t

y =ln x, ρ(x, y) =3xey , x =1, x = 2 ;

4cos t

, ρ(x, y) =

, t1 = 0, t2

π .

4sin t

y = ln cos x, ρ(x, y) =1, x

= −

π , x

= π ;

−t / 2

, ρ(x, y) =

, t1 = ln 3, t2 = ln 8.

−t

y = e

x2 y

y =ln(x2 −1), ρ(x, y) =1, x

=3, x

=5 ;

x = e

ρ(x, y)

, t1

ln 8, t2

ln 24 .

−t

y = e

7. а) y = 2 x, ρ(x, y) =

6x , x

3, x =15 ;

x = ln t

3ex

, ρ(x, y) =

, t1 =1, t2 = 2 .

б)

y =

8. а) y =

, ρ(x, y) = 6x2 3 3y , x = 0, x =1;

= cos

ρ(x, y) =16 2(x − y), t1 = 0, t2

б)

=sin2 t

= π , x

= 5π ;

9. а) y = ln sin x, ρ(x, y) =1,

/ 2

, ρ(x, y)

=3, t1 = 2 2, t2 = 2 6 .

б)

=t3 / 3

10. а) y =

(x, y) =

6x3

, x

4 3, x

= 4 8 ;

x = 2(t −sin t)

ρ(x, y) =1, t1 =0, t2 =π .

б)

= 2(1−cos t)

11. а) y =

, ρ(x, y) =

, x

= 1 , x

y2 + 4x2

= e

−t

, ρ(x, y) = 2 ,

t1 =ln

, t2

=ln 3 .

б)

= et

12. а) y =ex , ρ(x, y) =1, x =ln

3, x =ln 8 ;

x = 2

, ρ(x, y) = 1+

xy, t1 =1, t2 = 4 .

б)

13. а) y = x2 ,

ρ(x, y) =

, x

= 2, x

30 ;

1+ 4 y

x =1−cos t

, ρ(x, y) =1, t1 =0, t2 =π .

б)

=t −sin t

14. а)

y =ln(1− x2 ), ρ(x, y) =1, x

=0, x

=0, 2

;

б)

x =sin t +cos t , ρ(x, y) = x2 − y2 , t

= 0, t

= π .

=sin t −cos t

12 y

15. а)

y = x3 , ρ(x, y) =

, x

= 0, x

;

9xy

4 3

(x + y)

x = e

ρ(x, y)

, t1

=ln 3, t2 =ln 8 .

б)

y = e

−t

= 1

= 7 ;

16. а)

y = 1− x2 +arccos x, ρ(x, y) =1, x

, x

1,5t

−1

б)

x =

, ρ(x, y) =

, t1 =ln 8, t2 =ln 80 .

y = e

17. а)

y =

x, ρ( x, y) =

6 y2

x = 2, x

= 6 ;

x = cos t −sin t

ρ(x, y) = xy 2 ,

t1 = 0, t2 =

б)

=sin t +cos t

18. а)

y =sin x, ρ(x, y) =

x = 0, x =π ;

2 − y2

x = e

ρ(x, y) =

t1 =0, t2 =ln 3 .

б)

= 0,5e2t

8 , x = 35 ;

19. а)

y = 2x

x, ρ(x, y) =1,

x = arctgt

, ρ(x, y) =1, t1 = 0, t2 =1.

б)

= 0,5ln(1+t2 )

20. а)

y =

−

2x, ρ(x, y) =

x =8, x =18 ;

x2 +1

= t

−2t

x − y

б)

ρ( x, y) =

t1 =1, t2 = 7 .

= t2 +

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.03.2016345.13 Кб87Тиоповой расчёт по математике 6 модуль.pdf
#
20.03.2016912.38 Кб45Типовик - несобственные интегралы и ряды.doc
#
20.03.20163.06 Mб25типовик 1 курс 3 модуль.doc
#
20.03.20163.08 Mб69Типовик 3 модуль.doc
#
20.03.2016117.25 Кб36типовик 7 модуль.doc
#
14.04.20151.22 Mб184Типовик матан 5 модуль.pdf
#
21.03.201616.17 Mб23Типовик по матану 3 семестр.pdf
#
01.05.2025546.82 Кб0типовик.doc
#
21.03.201648.03 Mб134Типовик_мат_6модуль.pdf
#
14.04.2015988.75 Кб25ТИПОВЫЕ РАСЧЕТЫ ДЛЯ ЭКОНОМ СПЕЦ 1-2 модуль.pdf
#
14.04.20151.14 Mб29Типовые расчеты.pdf