Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2014 Модуль 3 Tipovik_III_LAST11

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Раздел 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Задание 13. Нахождение несобственных интегралов:

а) по бесконечному промежутку интегрирования, б) от неограниченной на отрезке функции.

А. Напомним, что несобственные интегралы по бесконечному промежутку определяются посредством предельного перехода. Ограничимся рассмотрением непрерывных на промежутке функций.

Если функция непрерывна на промежутке , то

Если функция непрерывна на всей числовой оси, то

Если предел существует и конечен, то несобственный интеграл называют сходящимся, если же предел не существует или бесконечен, то интеграл называют расходящимся.

Пример 1. Найдите значение несобственного интеграла или установите его расходимость: .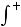

Решение. По определению несобственного интеграла имеем

Так как этот предел не существует, несобственный интеграл расходится.

Пример 2. Найдите значение несобственного интеграла Решение: По определению несобственного интеграла имеем

Для нахождения значения исходного интеграла мы применили формулу


интегрирования	по	частям	,	а	также

воспользовались правилом Лопиталя для отыскания предела				lim	lnb	.
					2

b	2b

Пример 3. Найдите значение несобственного интеграла

Решение: Подынтегральная функция чѐтная, поэтому можно воспользоваться свойством несобственных интегралов по симметричному промежутку от чѐтных функций

Б. Значения несобственных интегралов от неограниченных в окрестности некоторой точки функций также определяются посредством предельного перехода.

Если функция	непрерывна на	и	lim f (x)	, то
		x	a 0

Если функция	непрерывна на	и lim f (x)	, то
		x b 0

Если функция непрерывна на отрезке всюду, за исключением точки , и хотя бы один из односторонних пределов функции в этой точке бесконечен, то

Несобственный интеграл называют сходящимся, если его значение существует и конечно, и расходящимся в противном случае.

Пример 1. Найдите значение несобственного интеграла или установите его расходимость.

Решение: Функция f (x)	1	непрерывна при	1 x 0 и 0 x 2 и имеет
	x

бесконечные односторонние пределы в точке x			0 . Тогда

2 dx

0 dx

lim

lim ln

1 x

limln

lim ln 2 ln

Несобственные интегралы

0 dx

2 dx

расходятся, значит,

расходится и

1 x

0 x

исходный интеграл.

Пример 2. Найдите значение несобственного интеграла.

x(1

Решение: Функция

непрерывна при

и имеет

бесконечные односторонние пределы

. Тогда,

чтобы упростить запись решения, заменим сумму двух пределов одним пределом с двумя условиями и .

Часть 2. ТИПОВЫЕ ЗАДАНИЯ

Задание 1. Проинтегрируйте методом внесения под знак дифференциала.

1.sin x dx 2 cos x

2. x2 3 x3 dx

3.arcsin3 x dx

1 x2

4.(ln ln x)3 dx

xln x

5. xdx

cos2 (2x2 1)

6.			x		dx

	2		x4
7.		e3x dx
	1		e6 x
8.		(4x 1) dx


			x2	2

9.e3cos x sin xdx

10. e 3 x 1 dx

16.(1 ctg3 x) dx

sin2 x

17. (3x 3 x )dx

3x 3 x

18. (arccos x 1)dx

1 x2

19. 5 32 x 3 dx

20.	2 arcctg	2	x
		2
				dx
	1 x2			dx
	1 x2

21. dx

1 x2 arccos2 x

22.etgx 2

cos2 x dx

23.e2sin x cos xdx

24.

2 x

25.

2x 1 e

3x2

3x 4

11.

26.

sin

12.

27.

ln(2x

x 1

ln x

2,5

13.

28.

sin x

arctg

3cos x

14.

cos x

29.

(3x

1) dx

2sin x

3 x2

15.

ectgx

30.

x3 ln(x 4

1)dx

sin2 x

Задание 2. Найдите интеграл от тригонометрической функции:

sin

4 3x

16.

sin

3 dx

sin3x

cos x dx

17.

cos4x cos5xdx

sin5 2x

cos2x dx

18.

sin3 (x 1)

cos2 (x

sin2 3x

cos2 3x dx

3 cos2x sin 2x dx

19.

20.

sin x

sin6x dx

sin

6.		4 x			x
	sin			cos		dx
		2			2
7.	sin	3 4x		dx
			5

8. cos x cos3x dx

9.		cos5x				dx
9.
	4
	4		sin5x
10.	cos			2 x		1 dx
	cos				2	1 dx
					2

11.sin3x cos2x dx

12.cos3 2x dx sin2 2x

13.cos3 2x dx

14.sin7x sin5x dx

15.sin5 x cos3 x dx


21.	3 sin x	cos x dx
22.	sin2 (2x	1) cos2 (2x 1)dx

23.sin 2x cos 52x dx

24.cos3 6x sin2 6x dx

25.cos5 x sin x dx

26.cos 4x cos 8x dx

27.sin 5x cos 35x dx

28.sin3 5x cos3 5x dx

29.cos4 2x dx

30.cos4 x sin2 x dx

Задание 3.		Найдите интеграл:
1.	(3x	2)dx	16.	(4x	1)dx


	2x2
	2x2	4x 16		9x2	3x 2
			46

2)dx

17.

(2x

5)dx

3x2

6x 4

4 2x 2x2

(7x

5)dx

18.

(3x

2)dx

3 2x x2

4x2

2x 3

(2x

3)dx

19.

x)dx

5x 2

1 6x 7x2

3x) dx

20.

x)dx

2x2

3 2x 5x2

2x 1

(5x

1)dx

21.

3x) dx

4x2

x 2x2

3x)dx

22.

x)dx

4x 2

3x2

2x 5

x) dx

23.

(2x

1)dx

4 6x 4x2

7x 3 2x2

6x)dx

24.

(7x

6)dx

5x2

10.

(2 3x)dx

25.

(3x

1) dx

6x2

11.

(6x

1)dx

26.

1) dx

3x2

4x 2

2 5x 3x2

12.

(4x

1)dx

27.

(2x

5)dx

4 x 3x2

x 2x2

13.

(4x

3)dx

28.

x)dx

3x2

2x2

x 6

2x 1

14.	(4		x)dx	29.		(x	4)dx


		1 4x 5x2			1 3x 4x2
15.	(3		x)dx	30.		(6x	1)dx


	3x2
	3x2		6x 4			2 3x 2x2

Задание 4.

Найдите интеграл от дробно-рациональной функции:

(2x3

3x2

3)dx

16.

x(x

1) dx

(x 2)2 (x2

3x 5)

(x4

1)dx

17.

(x3

7x2

10)dx

(x 1)3 (x2

x3 (x2

(x4

3x3

2) dx

18.

(4x4

5x2

21x

10) dx

(x 1)(x4

x2 (x

2)(x2

(x2

22)dx

19.

(x2

10x

1) dx

(x 1)2 (x2

2x 5)

(x 2)2 (x2

x 3)

2(x2

4)dx

20.

(x3

4x2 6x

2) dx

x2 (x

1)(x2

x3 (x2

4x2

21.

(x4

23x2

32x

18) dx

1)(x4

x(x

3)2 (x2

(x2

2x3

11)dx

22.

x(x

4) dx

(x 2)2 (x2

3x 8)

(x3

4x2

2)dx

23.

(3x3

9x2

1) dx

(x 2)2 (x2

x3 (x2

2x 3)

9.	(5x3	10x2	8x 15) dx
	x2 (x	3)(x2	4x 5)

10.	(x3		7x	2)dx
	(x	1)2 (x2		2x 5)
11.	(x3	6x2		2x	4)dx
			x3 (x2	2)
12.	(x4	5x2 9x			4) dx
	x(x 1)2 (x2			2x 2)
13.	(2x3		x	7)dx
	(x	1)2 (x2		x	5)
14.	(x3	5x2		3x	6)dx
		x3 (x2		3)
15.	(8x2		6x3	3x	40) dx
	x(x 2)2 (x2				4x 5)

24.

(2x3

6x2

10x

9) dx

1)2 (x2

25.

(x2

1) dx

(x 1)2 (x2

26.

(3x3

7x2

9x 3) dx

1)2 (x2

27.

(x4

8x2

4) dx

x(x

1)2 (x2

28.

(x2

18x

20) dx

(x 2)2 (x2

29.

(2x3

3x2

3)dx

1)2 (x2

30.

2x(x3

12) dx

2)(x4

16)

Задание 5. Найдите интеграл от иррациональной функции:

1.				6										16.		x
1.				6			x			3		1	dx	16.		x					dx

															2		2x		1
										3
			x	3 1						3		x 3
2.														17.
2.			x	1				dx						17.	x		3x		2		10		dx
			x	1											x		3x		2		10

	x x					1									3x				2		7
	x x					1									3x				2		7
3.														18.
3.	5				x	1					dx			18.	6			x	2			dx
	5				x	1									6			x	2
				1 2												2)2
		x		1 2					x						(x	2)2				x	1
														49

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.2018132.48 Кб182-23_сетевые адаптеры.docx
#
21.03.2016669.87 Кб92-задания.pdf
#
20.03.2016172.54 Кб82.doc
#
21.03.2016397.47 Кб102012-10_ES_Razvitie_Innovats_Sistemy__17_str.Pdf
#
22.05.2015637.74 Кб152013 Модуль 4.pdf
#
14.04.20154.7 Mб142014 Модуль 3 Tipovik_III_LAST11.pdf
#
21.03.2016103.72 Кб82014_03_03_-_Java_IO.pdf
#
14.04.201528.67 Кб402014_Lab4_Manual.doc
#
14.04.20151.09 Mб122014_Lab6_Manual.pdf
#
14.04.20151.15 Mб112015UML06.pdf
#
14.04.20151.02 Mб42015UML07.pdf

1.				6										16.		x
1.				6			x			3		1	dx	16.		x					dx

															2		2x		1
										3
			x	3 1						3		x 3
2.														17.
2.			x	1				dx						17.	x		3x		2		10		dx
			x	1											x		3x		2		10

	x x					1									3x				2		7
	x x					1									3x				2		7
3.														18.
3.	5				x	1					dx			18.	6			x	2			dx
	5				x	1									6			x	2
				1 2												2)2
		x		1 2					x						(x	2)2				x	1
														49

1.				6										16.		x
1.				6			x			3		1	dx	16.		x					dx

															2		2x		1
										3
			x	3 1						3		x 3
2.														17.
2.			x	1				dx						17.	x		3x		2		10		dx
			x	1											x		3x		2		10

	x x					1									3x				2		7
	x x					1									3x				2		7
3.														18.
3.	5				x	1					dx			18.	6			x	2			dx
	5				x	1									6			x	2
				1 2												2)2
		x		1 2					x						(x	2)2				x	1
														49

1.				6										16.		x
1.				6			x			3		1	dx	16.		x					dx

															2		2x		1
										3
			x	3 1						3		x 3
2.														17.
2.			x	1				dx						17.	x		3x		2		10		dx
			x	1											x		3x		2		10

	x x					1									3x				2		7
	x x					1									3x				2		7
3.														18.
3.	5				x	1					dx			18.	6			x	2			dx
	5				x	1									6			x	2
				1 2												2)2
		x		1 2					x						(x	2)2				x	1
														49