
- •Средняя пространственная частотная характеристика рефлектограммы с одинарным зондирующим импульсом The Average spatial backscattered intensity spectrum of the otdr with single-pulse probe signal
- •Средняя пространственная частотная характеристика рефлектограммы с двухимпульсным зондирующим сигналом с частотным разнесением
- •Метод восстановления сигнала внешнего фазового воздействия на оптическое волокно в рефлектометре с двухимпульсным зондирующим сигналом с частотны мразнесением
- •Экспериментальные средние спектральные характеристики рефлектограмм.
- •Восстановление сигнала внешнего фазового воздействия методом квадратурной демодуляции
- •Заключение
-
Метод восстановления сигнала внешнего фазового воздействия на оптическое волокно в рефлектометре с двухимпульсным зондирующим сигналом с частотны мразнесением
The technique of external impact signal reconstruction in the OTDR with dual-pulse frequency diverse probe signal
Consider an
arbitrary small region of the fiber optic line
 which is exposed to an external phase impact, represented by a
tension of fiber according to some law
which is exposed to an external phase impact, represented by a
tension of fiber according to some law
 . The forward propagating dual-pulse with different carrier
frequencies of its first
. The forward propagating dual-pulse with different carrier
frequencies of its first
 and second
and second
 parts, fugure1 after some time will transfer into
the fiber region which is exposed by the external perturbation. For
simplicity we assume that the spatial extension of the perturbed
region is lesser
than the spatial extension of the probe pulse, i.e. consider the
external impact pointed. Without loss of generality, we assume the
registration and the digitization of the backscattered signal is made
only in those concrete moments of time when perturbation point
parts, fugure1 after some time will transfer into
the fiber region which is exposed by the external perturbation. For
simplicity we assume that the spatial extension of the perturbed
region is lesser
than the spatial extension of the probe pulse, i.e. consider the
external impact pointed. Without loss of generality, we assume the
registration and the digitization of the backscattered signal is made
only in those concrete moments of time when perturbation point
 is
just between the scattering regions of the first
is
just between the scattering regions of the first
 and the second
and the second
 parts of the dual-pulse , figure 3.
parts of the dual-pulse , figure 3.
External
action in the point
 leads
to additional phase modulation of the field, backscattered by the
fiber scattering region
leads
to additional phase modulation of the field, backscattered by the
fiber scattering region
 , while the field, backscattered by the scattering region
, while the field, backscattered by the scattering region
 ,
is not subjected to phase modulation. The electric fields,
backscattered by these regions under the assumption of polarization
degree and state preservation, in accordance with 32 и
33 will be as follows.
,
is not subjected to phase modulation. The electric fields,
backscattered by these regions under the assumption of polarization
degree and state preservation, in accordance with 32 и
33 will be as follows.
 3939\* MERGEFORMAT (),
3939\* MERGEFORMAT (),
 4040\* MERGEFORMAT (),
4040\* MERGEFORMAT (),
where
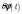 -
is the signal proportional to the external impact with the
proportionality coefficient
-
is the signal proportional to the external impact with the
proportionality coefficient
 ,
which includes the wave number for the second pulse of the pair
,
which includes the wave number for the second pulse of the pair
 .
In accordance with 35, the resulting intensity,
backscattered
by the two fiber scattering regions, around the perturbation point
.
In accordance with 35, the resulting intensity,
backscattered
by the two fiber scattering regions, around the perturbation point is
given by:
is
given by:
 4141\* MERGEFORMAT ().
4141\* MERGEFORMAT ().
The
signal registered by the OTDR 41 is quasi-harmonic, due to its
bandpass character as mentioned above. The FWHM of this bandpass
signal is defined by the shapes of double probe pulse, in the case
when these shapes are both rectangular, the average spatial power
spectrum of the OTDR intensity trace in the region near the carrier frequency
in the region near the carrier frequency
 is
defined by the second part of the expression 22, in the case when
these shapes are both Gaussian,
the average OTDR power spectrum near the frequency
is
defined by the second part of the expression 22, in the case when
these shapes are both Gaussian,
the average OTDR power spectrum near the frequency
 is defined by the second part of the expression 26. The FWHM of
the average spatial OTDR power spectrum in the second case is
narrower than in the first case. We should point out that these
spatial spectral characteristics are calculated on average over the
ensemble of independent distribution of scattering centers
is defined by the second part of the expression 26. The FWHM of
the average spatial OTDR power spectrum in the second case is
narrower than in the first case. We should point out that these
spatial spectral characteristics are calculated on average over the
ensemble of independent distribution of scattering centers
 which
change under environmental influence. In the real OTDR system the
fiber optic line is usually in quasi stationary conditions with some
steady temperature distribution along the fiber, which means that
only one random distribution of scattering centers
which
change under environmental influence. In the real OTDR system the
fiber optic line is usually in quasi stationary conditions with some
steady temperature distribution along the fiber, which means that
only one random distribution of scattering centers
 contributes in the OTDR intensity trace formation. Found PSDs 20
and 38 indicate what spatial harmonics may be contained in the OTDR
spatial power spectrum and their average power over the ensemble
contributes in the OTDR intensity trace formation. Found PSDs 20
and 38 indicate what spatial harmonics may be contained in the OTDR
spatial power spectrum and their average power over the ensemble
 .The narrower these PSDs are the more harmonic appearance the OTDR
intensity traces will have (with the oscillation frequency
.The narrower these PSDs are the more harmonic appearance the OTDR
intensity traces will have (with the oscillation frequency
 ),
this behavior can also be interpreted as OTDR “signal coherence”,
bearing in mind that this “coherence” related to the intensity
spatial behavior, figure 2 b).
),
this behavior can also be interpreted as OTDR “signal coherence”,
bearing in mind that this “coherence” related to the intensity
spatial behavior, figure 2 b).
The phase
error that occurs after the synchronous detection of the bandpass
OTDR signal with the carrier frequency
 ,
and FWHM of the average spatial spectrum
,
and FWHM of the average spatial spectrum
 after
one period of carrier oscillation
after
one period of carrier oscillation could
be estimated as:
could
be estimated as:
 .
In order to detect the small perturbation signals
.
In order to detect the small perturbation signals
 the
following relation must be satisfied:
the
following relation must be satisfied:
 4242\* MERGEFORMAT (),
4242\* MERGEFORMAT (),
this
condition is valid either in the case of small FWHM
 of
average OTDR spatial power spectrum or in the case of large carrier
frequencies difference
of
average OTDR spatial power spectrum or in the case of large carrier
frequencies difference
 between the dual pulse parts
between the dual pulse parts and
and
 .
.
The external
perturbation signal
 can
now be extracted by means of quadrature
or I/Q demodulation which involves the measurement and processing of
in-phase component or I-component and quadrature component or
Q-component of the OTDR intensity trace
can
now be extracted by means of quadrature
or I/Q demodulation which involves the measurement and processing of
in-phase component or I-component and quadrature component or
Q-component of the OTDR intensity trace
 [12]. In the absence of external action the intensity trace 41
represents quasi-harmonic signal of spatial coordinate
[12]. In the absence of external action the intensity trace 41
represents quasi-harmonic signal of spatial coordinate
 ,
which experiences random drift due to random changes of backscattered
fields amplitudes and phases.
,
which experiences random drift due to random changes of backscattered
fields amplitudes and phases.
External
action in the region
 will
cause the phase change of this quasi-harmonic signal. I and Q-
components can be obtained via multiplication of the registered
signal
will
cause the phase change of this quasi-harmonic signal. I and Q-
components can be obtained via multiplication of the registered
signal
 in the radio domain by two harmonic radio signals differing in phase
by
in the radio domain by two harmonic radio signals differing in phase
by :
i.e.
:
i.e.
 and
and
 and
subsequent low-pass filtering of these products [12]. As a result the
terms with frequencies:
and
subsequent low-pass filtering of these products [12]. As a result the
terms with frequencies:
 and
and
 will
not be included in the expression for I and Q-components that will
take the form:
will
not be included in the expression for I and Q-components that will
take the form:
 4343\* MERGEFORMAT (),
4343\* MERGEFORMAT (),
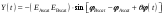 4444\* MERGEFORMAT ().
4444\* MERGEFORMAT ().
Provided
that the result
of the backscattered amplitudes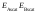 is
different from zero, the total phase change can be calculated as:
is
different from zero, the total phase change can be calculated as:
 4545\* MERGEFORMAT (),
4545\* MERGEFORMAT (),
the
small value of the additional phase is
ensured by the condition 42. Note that the range of the
is
ensured by the condition 42. Note that the range of the
 function in 45 is
function in 45 is
 for
this reason the calculated phase
for
this reason the calculated phase
 45
is restricted to this interval, whereas the real external action,
measured in radians, can be far beyond this interval. So in order to
obtain the actual value of the phase action it is necessary to
perform the unwrapping procedure which implies the correction of
radian phase angle
45
is restricted to this interval, whereas the real external action,
measured in radians, can be far beyond this interval. So in order to
obtain the actual value of the phase action it is necessary to
perform the unwrapping procedure which implies the correction of
radian phase angle
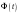 by adding multiples of
by adding multiples of
 when the jumps of
when the jumps of
 in consecutive values of
in consecutive values of
 occur.
The external signal can also be restored with using
the procedure which utilizes cross-derivatives, described in [4].
occur.
The external signal can also be restored with using
the procedure which utilizes cross-derivatives, described in [4].
From 43 and
44 it is seen that when the result
of backscattered amplitudes
 is close to zero, the external signal is undefined, in this case a
so-called signal fading takes place. One of the main ways to
overcome fading is the variation of the laser source wavelength.
is close to zero, the external signal is undefined, in this case a
so-called signal fading takes place. One of the main ways to
overcome fading is the variation of the laser source wavelength.
