
- •Средняя пространственная частотная характеристика рефлектограммы с одинарным зондирующим импульсом The Average spatial backscattered intensity spectrum of the otdr with single-pulse probe signal
- •Средняя пространственная частотная характеристика рефлектограммы с двухимпульсным зондирующим сигналом с частотным разнесением
- •Метод восстановления сигнала внешнего фазового воздействия на оптическое волокно в рефлектометре с двухимпульсным зондирующим сигналом с частотны мразнесением
- •Экспериментальные средние спектральные характеристики рефлектограмм.
- •Восстановление сигнала внешнего фазового воздействия методом квадратурной демодуляции
- •Заключение
A phase-sensitive optical time-domain reflectometer with dual-pulse diverse frequency probe signal.
A E Alekseev1, 2, V S Vdovenko2, B G Gorshkov3, V T Potapov1 and D E Simikin2
1 Kotel’nikov Institute of Radio Engineering and Electronics, Russian Academy of Sciences, Vvedensky Sq. 1, Fryazino, Moscow region, Russia
2Petrofibre Ltd., Klinskiy proezd, 7, Novomoskovsk, Tula region, Russia
3Prokhorov General Physics Institute, Russian Academy of Sciences, Vavilov Str., 38, Moscow, Russia
E-mail: aleksey.e.alekseev@gmail.com
Abstract
In the present letter we propose a novel approach for realization of a phase sensitive optical time-domain reflectometer (OTDR) which is capable of precise reconstruction of a phase signal which impacts the arbitrary point of a fiber-optic line. The method implies using a dual-pulse probe signal with diverse carrier optical frequency within each half of the double pulse. The quasi-periodic intensity pattern which emerges as a result of double frequency backscattered signal interference contains the information of the external action over the fiber. The phase signal is extracted with an aid of I/Q quadrature demodulation scheme, realized on the receiving side of the OTDR. The feasibility and limitations of the proposed scheme are theoretically proved and experimentally demonstrated.
Keywords: optical time-domain reflectometer, fiber optic sensor, power spectral density, I/Q demodulation.
-
Introduction
Currently there has been proposed
several realizations of a phase-sensitive OTDR, which enable
reconstruction of the phase signal which impacts the optical fiber.
One of these methods implies using
a six-port optical hybrid that is placed in the receiving part of the
OTDR in conjunction with an unbalanced Mach–Zehnder or Michelson
interferometer [1-3]. The hybrid is conventionally represented by a
symmetric 3 x 3 coupler, which shifts the phases of interfering
signals relative to each other and enables to perform a phase
diversity technique for external signal reconstruction. The
limitations of this scheme are (related
with the)\(coming from the)
necessity of using of
three independent photodetectors and consequently three independent
detection schemes which have to be fully synchronized. The unbalanced
interferometer in the receiving part of OTDR is sensitive to
environmental perturbations and requires serious thermally and
vibration isolation, moreover, to avoid polarization fading of
detected signal the additional means for polarization matching have
to be taken.
In the previous paper we proposed another realization of OTDR with the possibility of external impact signal reconstruction; the scheme implied using double pulse probe signal which had different phase shifts for the first and the second pulses of the pair [4]. The required phase difference between the pulses within the probe pulse pair was reached via a phase modulator after the double pulse source, the detected backscattered signals at the output of the OTDR consequently became phase shifted relative to each other, which enabled to perform the phase diversity technique for external impact signal reconstruction. In comparison with previously mentioned one, the advantage of this scheme is absence of applying of optical hybrid, unbalanced interferometer and three independent photodetectors in the receiving end, which significantly simplifies the scheme and makes it more sustainable to environmental fluctuations. The scheme limitations include requirement to use three independent pulse pairs with different relative phase shifts for correct registration of the single external impact signal time sample. Consequently the maximum detectable frequency or effective external signal bandwidth, capable of registration, is three times less than in hybrid schemes, described above.
Another approach to realization of a phase-sensitive OTDR, first mentioned in [5], is applying a double pulse probe signal, with the carrier frequencies of pulses, constituting the pair, shifted relative to each other over a certain value, unlike the previous scheme [4] where only the phases of these pulses are shifted. This solution with diverse frequency dual-pulse probe signal enables to reduce the number of independent pulse pairs required for correct registration of the single time sample of an external impact to one, thus three times enlarging the maximum frequency or effective external signal bandwidth, capable of registration, comparing with phase shift method [4]. As a result, this scheme is free from drawbacks of both the scheme with optical hybrid and the scheme with phase manipulation and looks promising for realization of high performance phase-sensitive OTDR.
Despite the method with two carrier frequencies was firstly mentioned in [5], it was not elaborated and somehow demonstrated experimentally. This article (paper), apparently, is the first detailed theoretical and experimental description of the phase-OTDR with dual-pulse diverse frequency probe signal.
-
Средняя пространственная частотная характеристика рефлектограммы с одинарным зондирующим импульсом The Average spatial backscattered intensity spectrum of the otdr with single-pulse probe signal
The operation of proposed phase-sensitive OTDR is based on the usage of double-pulse probe signal with different carrier frequencies of the first and the second parts of the pair. The carrier frequency difference must be aligned with the spatial spectrum of OTDR signal in a certain way. Thus firstly consider the spatial spectral characteristics of backscattered intensity OTDR traces, formed at the output, when a single probe pulse of a certain form, duration and fixed carrier frequency is used. In other words, define the spatial harmonics, constituting backscattered OTDR spatial traces. Then we will define the spectral characteristics of OTDR traces obtained when utilizing a double pulse with different carrier frequencies.
Extended optical fiber can be
modeled as a set of scattering centers, randomly distributed along
the length of the fiber. Consider an optical fiber of a length
 with
embedded random scattering centers axial distribution
with
embedded random scattering centers axial distribution
 ,
this distribution can be characterized by the set of complex
amplitude backscattering coefficients
,
this distribution can be characterized by the set of complex
amplitude backscattering coefficients
 ,
where
,
where
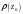 is complex amplitude backscattering coefficient of the scattering
center with longitudinal coordinate
is complex amplitude backscattering coefficient of the scattering
center with longitudinal coordinate
 , note that this distribution can change to another statistically
equivalent distribution under environmental influence. In the
introduced model of scattering medium we consider
, note that this distribution can change to another statistically
equivalent distribution under environmental influence. In the
introduced model of scattering medium we consider
 as
zero-mean circular complex Gaussian random variable (CCG) [6-10],
which means that real and the imaginary parts of
as
zero-mean circular complex Gaussian random variable (CCG) [6-10],
which means that real and the imaginary parts of
 :
: ,
,
 are
both have Gaussian ensemble distributions with equal variances. The
phase of such random variable obeys uniform statistics on the
interval
are
both have Gaussian ensemble distributions with equal variances. The
phase of such random variable obeys uniform statistics on the
interval
 .
Physically these assumptions represent the backscattering process as
multiplication of complex amplitude of the source field to random
values, having Gaussian distributions of a real and imaginary parts
with zero-mean. Let us also consider complex amplitude backscattering
coefficients as statistically uncorrelated [8, 9]. Mathematically the
lack of correlation between complex backscattering coefficients with
coordinates
.
Physically these assumptions represent the backscattering process as
multiplication of complex amplitude of the source field to random
values, having Gaussian distributions of a real and imaginary parts
with zero-mean. Let us also consider complex amplitude backscattering
coefficients as statistically uncorrelated [8, 9]. Mathematically the
lack of correlation between complex backscattering coefficients with
coordinates
 and
and
 and equality of real and imaginary parts variances can be expressed
in two expressions:
and equality of real and imaginary parts variances can be expressed
in two expressions:
 11\* MERGEFORMAT (),
11\* MERGEFORMAT (),
 22\* MERGEFORMAT (),
22\* MERGEFORMAT (),
where
 - denotes the average over the ensemble of independent distributions
of scattering centers
- denotes the average over the ensemble of independent distributions
of scattering centers
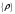 (or
over the ensemble of independent scattering mediums ) i.e. ensemble
average,
(or
over the ensemble of independent scattering mediums ) i.e. ensemble
average,
 ,
, - are axial coordinates of scattering centers,
- are axial coordinates of scattering centers,
 - is the variance of real or imaginary parts of backscattering
coefficients
- is the variance of real or imaginary parts of backscattering
coefficients
 ,
,
 - is the delta function.
- is the delta function.
Let us assume, for simplicity, that the source of optical field is fully monochromatic and that the state of optical field polarization is preserved during field propagation along the fiber as well as in the act of scattering. The analytic representation of source field can thus be written as:
 33\* MERGEFORMAT (),
33\* MERGEFORMAT (),
where
 - is the source field intensity,
- is the source field intensity,
 - is the angular frequency of the source field radiation. The complex
amplitude of the field incident on the scattering center located at
the distance
- is the angular frequency of the source field radiation. The complex
amplitude of the field incident on the scattering center located at
the distance
 can
be written as:
can
be written as:
 44\* MERGEFORMAT (),
44\* MERGEFORMAT (),
where
 -
is the intensity attenuation coefficient,
-
is the intensity attenuation coefficient,
 -
is field propagation constant,
-
is field propagation constant,
 -
is field group velocity. The complex amplitude of backscattered field
in the point of scattering
-
is field group velocity. The complex amplitude of backscattered field
in the point of scattering
 is
given by [8]:
is
given by [8]:
 55\* MERGEFORMAT ().
55\* MERGEFORMAT ().
Let us consider that optical
pulse is characterized by amplitude function of time or equivalent
spatial coordinate with full width at half maximum (FWHM) equal to
 :
: ,
in the particular case this could be a rectangular pulse:
,
in the particular case this could be a rectangular pulse:
 66\* MERGEFORMAT (),
66\* MERGEFORMAT (),
or a Gaussian pulse
 77\* MERGEFORMAT ().
77\* MERGEFORMAT ().
The complex amplitude of the
field backscattered by the region of the optical fiber, occupied by
the optical pulse at the distance
 from the beginning can be expressed us:
from the beginning can be expressed us:
 88\* MERGEFORMAT (),
88\* MERGEFORMAT (),
Thus,
the complex amplitude of the backscattered field at the output of the
OTDR with the amplitude probe pulse form
 and FWHM
and FWHM
 for every fixed realization of scattering centers distribution
for every fixed realization of scattering centers distribution is
represented by the convolution of the complex amplitude function of
the optical field
is
represented by the convolution of the complex amplitude function of
the optical field
 , backscattered by the centers with longitudinal coordinates
, backscattered by the centers with longitudinal coordinates
 and
the function, which defines the shape of the probe pulse
and
the function, which defines the shape of the probe pulse .
In other words the random function of spatial coordinate
.
In other words the random function of spatial coordinate is
filtered by the linear filter with impulse response function
is
filtered by the linear filter with impulse response function .
When filtering on spatial coordinate, the spatial spectrum of the
signal
.
When filtering on spatial coordinate, the spatial spectrum of the
signal is
changed. Every new realization of the scattering centers distribution
is
changed. Every new realization of the scattering centers distribution
 in
the fiber leads to appearance of a new realization of the spatial
intensity distribution and consequently a new spatial spectrum of
OTDR trace. For
practical purposes spectral characteristics over the ensemble of
random OTDR intensity traces attract major interest.
in
the fiber leads to appearance of a new realization of the spatial
intensity distribution and consequently a new spatial spectrum of
OTDR trace. For
practical purposes spectral characteristics over the ensemble of
random OTDR intensity traces attract major interest.
To determine
the average spatial spectral characteristics of the OTDR traces
ensemble, consider the complex Gaussian random process with the sample function represented by single random distribution
of complex scattering coefficients
with the sample function represented by single random distribution
of complex scattering coefficients
 along the fiber. Each
new distribution of scattering centers
along the fiber. Each
new distribution of scattering centers
 leads to a new sample function of considered random process
leads to a new sample function of considered random process
 . The autocorrelation function (ACF) of the regarded process has the
form 2.
. The autocorrelation function (ACF) of the regarded process has the
form 2.
Multiplication
of the random Gaussian process
 with the sample function
with the sample function on
the deterministic function 4 leads to another Gaussian random
process
on
the deterministic function 4 leads to another Gaussian random
process with the sample function
with the sample function 5.
5.
The power
spectral density (PSD): of
the linearly filtered random process
of
the linearly filtered random process
 with the sample function 8 is determined according to [10]:
with the sample function 8 is determined according to [10]:
 99\* MERGEFORMAT (),
99\* MERGEFORMAT (),
where
 denotes
the Fourier transform of the impulse response
denotes
the Fourier transform of the impulse response
 i.e. the transfer function,
i.e. the transfer function,
 is the PSD of the random process
is the PSD of the random process
 .
.
To calculate the PSD of the
random process consider
its ACF, neglecting the intensity attenuation we obtain:
consider
its ACF, neglecting the intensity attenuation we obtain:
 1010\* MERGEFORMAT ().
1010\* MERGEFORMAT ().
From
10 it is seen that the ACF depends only on the coordinate
difference ,
thus the random process
,
thus the random process is wide-sense stationary and Wiener–Khinchin theorem can be applied
[10], according to which the Fourier transform of the ACF 10
results in the PSD:
is wide-sense stationary and Wiener–Khinchin theorem can be applied
[10], according to which the Fourier transform of the ACF 10
results in the PSD:
 of the random process
of the random process
 :
:
 1111\* MERGEFORMAT (),
1111\* MERGEFORMAT (),
The
PSD of the process
 is
then has the form:
is
then has the form:
 1212\* MERGEFORMAT (),
1212\* MERGEFORMAT (),
in case of the rectangular probe
pulse shape
 the
PSD is:
the
PSD is:
 1313\* MERGEFORMAT (),
1313\* MERGEFORMAT (),
in case of the Gaussian probe
pulse shape
 the PSD is:
the PSD is:
 1414\* MERGEFORMAT ().
1414\* MERGEFORMAT ().
Found expressions for the PSD
12, 13 and 14 shows what spatial harmonics on average over the
ensemble
 constitute the function
constitute the function
 which
represents the spatial distribution of complex backscattered fields
amplitudes over the length of the fiber in the assumption of very
long fiber so the spectral leakage caused by finite fiber length
which
represents the spatial distribution of complex backscattered fields
amplitudes over the length of the fiber in the assumption of very
long fiber so the spectral leakage caused by finite fiber length
 can be ignored.
can be ignored.
Let us now define the average
spectral characteristic of the OTDR intensity traces, formed when the
probe pulse with the time shape
 is used. The intensity of
the field 8, backscattered from the fiber region with spatial
coordinate
is used. The intensity of
the field 8, backscattered from the fiber region with spatial
coordinate
 is as follows:
is as follows:
 1515\* MERGEFORMAT (),
1515\* MERGEFORMAT (),
 -
denotes the time average, in 15 we used high coherence assumption
for the source field and so the intensity does not fluctuate in time
and time averaging can be omitted. Random spatial function
-
denotes the time average, in 15 we used high coherence assumption
for the source field and so the intensity does not fluctuate in time
and time averaging can be omitted. Random spatial function
 can also be regarded as the sample function of the random process
can also be regarded as the sample function of the random process ,
originated from the sample function
,
originated from the sample function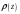 ,
which changes when a new distribution of scattering centers
,
which changes when a new distribution of scattering centers
 occurs. To calculate the PSD of this random process define its ACF:
occurs. To calculate the PSD of this random process define its ACF:
 1616\* MERGEFORMAT ().
1616\* MERGEFORMAT ().
Note that
linearly filtered process
 with the sample function
with the sample function
 is also Gaussian random process [10] and in compliance with 1 and
2 it is circular as well. Let us then use the Gaussian moment
theorem [11] for the complex scattering coefficients
is also Gaussian random process [10] and in compliance with 1 and
2 it is circular as well. Let us then use the Gaussian moment
theorem [11] for the complex scattering coefficients
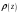 ,
which claims:
,
which claims:
 1717\* MERGEFORMAT (),
1717\* MERGEFORMAT (),
in case of four complex Gaussian values it takes the form:
 1818\* MERGEFORMAT ().
1818\* MERGEFORMAT ().
The fourth moment 16 can then be written in the form:
 1919\* MERGEFORMAT (),
1919\* MERGEFORMAT (),
where the square brackets contain
the ACF of the linearly filtered random process
 ,
which depends only on the coordinate difference
,
which depends only on the coordinate difference
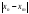 ,
thus the random process with the ACF 19 is also wide-sense
stationary and Wiener–Khinchin theorem can be applied again. The
PSD of the random process
,
thus the random process with the ACF 19 is also wide-sense
stationary and Wiener–Khinchin theorem can be applied again. The
PSD of the random process
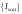 with the sample function
with the sample function
 will
be as follows:
will
be as follows:
 2020\* MERGEFORMAT ().
2020\* MERGEFORMAT ().
Found
expression shows what spatial harmonics on average over the ensemble
 constitute the spatial distribution of backscattered intensity
constitute the spatial distribution of backscattered intensity
 over the length of the fiber in the assumption of very long fiber to
neglect the spectral leakage effect. In other words 20 shows the
average
spatial power spectrum of the OTDR intensity trace.
over the length of the fiber in the assumption of very long fiber to
neglect the spectral leakage effect. In other words 20 shows the
average
spatial power spectrum of the OTDR intensity trace.
In the case of the rectangular probe pulse, the convolution in 20 could, for instance, be calculated with using of convolution theorem by the following steps: the Fourier transform, multiplication of the results and inverse Fourier transform:
 2121\* MERGEFORMAT (),
2121\* MERGEFORMAT (),
Taking 13 into account for the desired PSD we obtain:
 2222\* MERGEFORMAT ().
2222\* MERGEFORMAT ().
To estimate the FWHM of this average spatial power spectrum, one have to solve the transcendental equation, the final result is, as it follows:
 2323\* MERGEFORMAT (),
2323\* MERGEFORMAT (),
where
 is the FWHM of
the average spatial power spectrum of the OTDR intensity trace. Note
that the OTDR trace could be interpreted either as
intensity-to-distance dependence or intensity-to-time dependence, the
spectral width in time domain is obtained after multiplication of
23
by the group velocity of light:
is the FWHM of
the average spatial power spectrum of the OTDR intensity trace. Note
that the OTDR trace could be interpreted either as
intensity-to-distance dependence or intensity-to-time dependence, the
spectral width in time domain is obtained after multiplication of
23
by the group velocity of light:
 2E8 m/s, as a result we have:
2E8 m/s, as a result we have:
 2424\* MERGEFORMAT (),
2424\* MERGEFORMAT (),
 is the
duration of the rectangular probe pulse amplitude characteristic
is the
duration of the rectangular probe pulse amplitude characteristic
 .
Thus the rectangular probe pulse with amplitude characteristic
duration equal to
.
Thus the rectangular probe pulse with amplitude characteristic
duration equal to
 100
ns produces the OTDR trace with the FWHM of the average power
spectrum equal to 12 MHz. Note that for the rectangular probe pulse
the duration of amplitude
100
ns produces the OTDR trace with the FWHM of the average power
spectrum equal to 12 MHz. Note that for the rectangular probe pulse
the duration of amplitude
 and intensity
and intensity
 characteristic coincide, the spectral width of the initial intensity
probe pulse power spectrum
characteristic coincide, the spectral width of the initial intensity
probe pulse power spectrum is equal to:
is equal to:
 2525\* MERGEFORMAT (),
2525\* MERGEFORMAT (),
comparing
24 and 25 one can see that FWHM of the average OTDR trace power
spectrum
 exceeds the width of the power spectrum
exceeds the width of the power spectrum of
the initial rectangular probe pulse as much as 1.36 times, the
average
power spectrum of the OTDR intensity trace
broadens.
of
the initial rectangular probe pulse as much as 1.36 times, the
average
power spectrum of the OTDR intensity trace
broadens.
In the case of the Gaussian probe pulse less tedious calculations lead to the following PSD:
 2626\* MERGEFORMAT (),
2626\* MERGEFORMAT (),
the FWHM of this average spatial power spectrum can be calculated as:
 2727\* MERGEFORMAT (),
2727\* MERGEFORMAT (),
the
FWHM in time domain is obtained in the same way, multiplying 27 by
 :
:
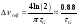 2828\* MERGEFORMAT (),
2828\* MERGEFORMAT (),
 is the
duration of the Gaussian probe pulse amplitude characteristic
is the
duration of the Gaussian probe pulse amplitude characteristic
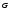 .
Thus the Gaussian probe pulse with amplitude characteristic duration
equal to
.
Thus the Gaussian probe pulse with amplitude characteristic duration
equal to
 100
ns produces the OTDR trace with the FWHM of average power spectrum
equal to 8.8 MHz. For the Gaussian probe pulse the duration of
amplitude
100
ns produces the OTDR trace with the FWHM of average power spectrum
equal to 8.8 MHz. For the Gaussian probe pulse the duration of
amplitude
 exceeds the duration of intensity
exceeds the duration of intensity
 characteristic as much as
characteristic as much as
 times,
the spectral width of the initial intensity probe pulse power
spectrum
times,
the spectral width of the initial intensity probe pulse power
spectrum is equal to:
is equal to:
 2929\* MERGEFORMAT (),
2929\* MERGEFORMAT (),
comparing
28 and 29 one can see that FWHM of average OTDR trace power
spectrum
 now equals to the width of power spectrum
now equals to the width of power spectrum of
the initial Gaussian probe pulse, the average
power spectrum of the OTDR intensity trace
preserves it width. In intermediate cases, when the probe pulse has,
for instance, Super-Gaussian shape the FWHM of
average power spectrum of the OTDR
intensity
trace will be within the limits defined by 28 and 24.
of
the initial Gaussian probe pulse, the average
power spectrum of the OTDR intensity trace
preserves it width. In intermediate cases, when the probe pulse has,
for instance, Super-Gaussian shape the FWHM of
average power spectrum of the OTDR
intensity
trace will be within the limits defined by 28 and 24.
-
The OTDR intensity trace for dual-pulse diverse frequency probe signal
Suppose,
the dual-pulse probe signal with different carrier frequencies of its
first and the second parts:
 and
and
 is launched into the OTDR fiber line, the corresponding field
propagation constants are
is launched into the OTDR fiber line, the corresponding field
propagation constants are
 and
and
 ,
figure 1. Denote the first and the second parts of the probe pulse by
the letters
,
figure 1. Denote the first and the second parts of the probe pulse by
the letters
 and
and .
We assume the time duration of pulses in the double pulse and the
time interval between them equal to
.
We assume the time duration of pulses in the double pulse and the
time interval between them equal to
 , that corresponds to the spatial duration equal to
, that corresponds to the spatial duration equal to
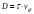 .
Consider an arbitrary time instance
.
Consider an arbitrary time instance
 when the pulse pair has moved to
when the pulse pair has moved to
 position from the beginning of the fiber line. The electric fields,
backscattered by the first
position from the beginning of the fiber line. The electric fields,
backscattered by the first
 and the second
and the second
 parts of the probe pulse, with the
assumption of monochromaticity and polarization preservation of the
pulse fields can be written in the form:
parts of the probe pulse, with the
assumption of monochromaticity and polarization preservation of the
pulse fields can be written in the form:
 3030\* MERGEFORMAT (),
3030\* MERGEFORMAT (),
 3131\* MERGEFORMAT (),
3131\* MERGEFORMAT (),
where
 and
and
 are defined by 8. Note that the optical fields backscattered by the
second part of the pulse pair
are defined by 8. Note that the optical fields backscattered by the
second part of the pulse pair
 and the first part
and the first part
 will have equal spatial positions near the point with coordinate
will have equal spatial positions near the point with coordinate ,
the first part of the probe pulse should then pass the distance
,
the first part of the probe pulse should then pass the distance
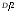 forward
while the backscattered fields of the second part of the probe pulse
should pass the same distance in the reversed direction. The
corresponding electric backscattered fields near the point of their
spatial superposition are, as
it follows:
forward
while the backscattered fields of the second part of the probe pulse
should pass the same distance in the reversed direction. The
corresponding electric backscattered fields near the point of their
spatial superposition are, as
it follows:
 3232\* MERGEFORMAT (),
3232\* MERGEFORMAT (),
 3333\* MERGEFORMAT (),
3333\* MERGEFORMAT (),
where
the complex amplitudes of the backscattered fields
 and
and
 are equivalently denoted by
are equivalently denoted by
 and
and
 ,
where
,
where ,
,
 ,
, and
and
 ,
are the random amplitudes and the phases of the backscattered fields,
corresponding to the parts
,
are the random amplitudes and the phases of the backscattered fields,
corresponding to the parts
 an
an
 of the dual-pulse. When two spatially superimposed parts of
backscattered pulse reach the beginning of the fiber line, they both
pass double distance
of the dual-pulse. When two spatially superimposed parts of
backscattered pulse reach the beginning of the fiber line, they both
pass double distance
 ,
however this additional phase could be measured only with the
accuracy up to
,
however this additional phase could be measured only with the
accuracy up to
 and therefore does not change the uniform statistics of the fields
random phase distributions
and therefore does not change the uniform statistics of the fields
random phase distributions and
and
 on the interval
on the interval
 .
For this reason this additive phase could be omitted.
.
For this reason this additive phase could be omitted.
The sum intensity of backscattered fields at the beginning of the OTDR fiber line is found to be:
 3434\* MERGEFORMAT ().
3434\* MERGEFORMAT ().
Thus
at the output of the OTDR the quasi-harmonic time-dependent bandpass
signal is detected with the carrier frequency equal to
 ,
the power spectrum of this signal is broadened due to the random
changes of the amplitudes and the phases of the backscattered
fields:
,
the power spectrum of this signal is broadened due to the random
changes of the amplitudes and the phases of the backscattered
fields: ,
,
 ,
, and
and
 along the fiber. The cosine in 34 along with the regular
time-dependent phase component:
along the fiber. The cosine in 34 along with the regular
time-dependent phase component: contains
the random component:
contains
the random component: which
depends on the certain realization of the fiber scattering centers
distribution
which
depends on the certain realization of the fiber scattering centers
distribution
 . The expression 34 shows that OTDR trace, which emerges when a
dual-pulse with different carrier frequencies is
used
as a probe signal, has quasi-harmonic structure with a central
frequency equal to:
. The expression 34 shows that OTDR trace, which emerges when a
dual-pulse with different carrier frequencies is
used
as a probe signal, has quasi-harmonic structure with a central
frequency equal to: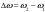 .
Since the time dependence of the backscattered intensity 34 is
interpreted by the OTDR as the distance dependence, the change of
variable could be made:
.
Since the time dependence of the backscattered intensity 34 is
interpreted by the OTDR as the distance dependence, the change of
variable could be made:
 ,
that leads to the following:
,
that leads to the following:
 3535\* MERGEFORMAT (),
3535\* MERGEFORMAT (),
where
there is only time-dependence on the spatial coordinate along the
fiber exists. Figure 2 shows the experimental OTDR traces, obtained
with using
dual-pulse probe signal, where each part of the double pulse has the
Gaussian shape with the time duration equal to 100
ns and the time interval between these parts also equal to
100
ns and the time interval between these parts also equal to 100
ns, with equal carrier frequencies of the two pulse parts figure. 2a)
and with different carrier frequencies of the two pulse parts, where
100
ns, with equal carrier frequencies of the two pulse parts figure. 2a)
and with different carrier frequencies of the two pulse parts, where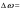 100 MHz figure 2 b). As
one can see,
frequency
spacing
100 MHz figure 2 b). As
one can see,
frequency
spacing
 of the dual-pulse parts leads to the oscillations of the OTDR
intensity trace with a characteristic frequency, determined by this
carrier frequency spacing
of the dual-pulse parts leads to the oscillations of the OTDR
intensity trace with a characteristic frequency, determined by this
carrier frequency spacing
 . At the same time the power spectrum of the resulting OTDR trace
broadens due to random amplitude and phase modulation of the carrier
. At the same time the power spectrum of the resulting OTDR trace
broadens due to random amplitude and phase modulation of the carrier
 ,
which is also seen on figure 2 b).
,
which is also seen on figure 2 b).
