Задания к лабам / 1 / ИТЗИлаб01

7

Московский государственный институт электронной техники

(технический университет)

Кафедра вычислительной техники

Дисциплина: «Инженерно-техническая защита информации»

(группы МП-33, 34)

Лабораторная работа №1

«Исследование модулированных сигналов, применяемых для скрытной передачи информации»

Составил: доцент Тельминов О.А.

Цель работы: получение навыков формирования и обработки сложномодулированных сигналов (в среде MATLAB).

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В процессе физической передачи информации актуальным является сокрытие самого факта передачи данных. При этом исходная посылка должна быть подготовлена к передаче, передана в эфир, принята и дешифрирована.

Маскировка для уменьшения заметности факта передачи информации должна снижать энергию сигнала, доступного средству разведки. Для этого в системах используются:

– возможно меньшие уровни излучения (обеспечиваются за счет выбора структур и свойств сигналов, а также особыми способами обработки сигналов в приемнике);

­– широкополосные сигналы, имеющие большую базу (F– девиация частоты или полоса частот, – период сигнала) и обеспечивающие большую параметрическую неопределенность для приемника средства разведки;

– снижение уровней побочных и непреднамеренных излучений электронных систем и средств объектов разведки.

Широкополосные сигналы занимают полосу частот, существенно превышающую полосу частот переносимого ими сообщения.

Расширение полосы частот сигнала достигается за счет модуляции несущего колебания по амплитуде, фазе или частоте.

Для передачи сообщений применяют сложные сигналы – линейные и нелинейные кодовые последовательности.

Типичными и наиболее распространенными являются М-последовательности (рис. 1), для которых справедливо рекуррентное правило:

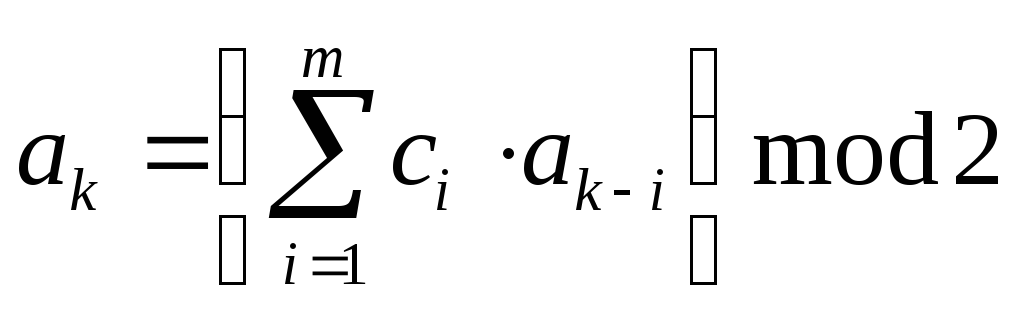, (1)

где – характеристический многочлен. Комбинация символов 00..000 является запрещенной, поскольку все последующие вычисления по выражению (1) приведут к нулевому результату.

В среде Matlab вектор задается как a = [1 0 0 0 0 0 0 0], доступ к элементу осуществляется путем индексирования: a(6), вычисление суммы по модулю – с помощью функции mod.

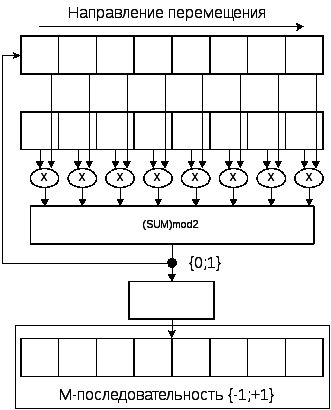
Рис. 1. Схема формирования М-последовательности

На основании полученной последовательности символов формируется расширяющая функция .

Таким образом, при длине характеристического многочлена период формируемой последовательности не может превышать символов.

Период М-последовательности . Ширина спектра М-последовательности определяется ее самым коротким элементом – символом и равна , в то время как база такого сигнала – .

Важными характеристиками М-последовательности являются свойства ее автокорреляционной функции (АКФ). Для ее построения используется математическая операция свертка. Свертка вычисляется как в частотной, так и во временной областях.

Схема вычисления свертки во временной области приведена на рис. 2. Если длины сворачиваемых последовательностей P и Q равны LP и LQ, то длина свертки равна LP+LQ–1.

АКФ формируется с помощью свертки М-последовательности самой на себя.

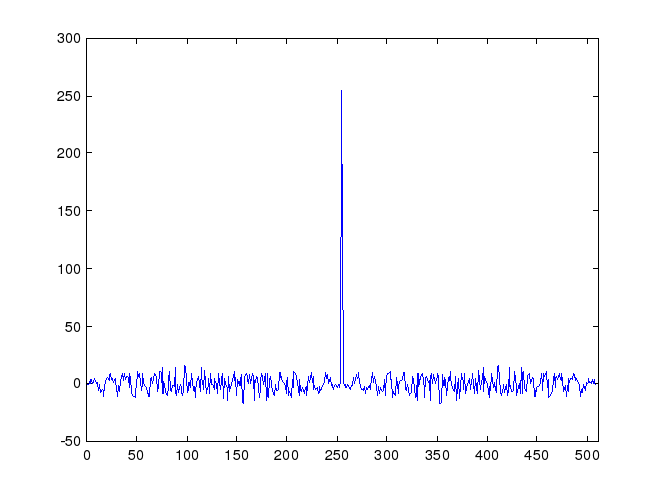
В качестве основных свойств АКФ являются величина пика и максимальный уровень боковых лепестков. На практике применяются М-последовательности, указанные величины АКФ для которых равны и соответственно (рис. 3).

Для выявления М-последовательностей при заданном значении m осуществляется перебор всевозможных вариантов характеристического многочлена С = 000…00 – 111…11. Для m=8 их число равно 256, однако не при всех С будет сформирована М-последовательность.

В среде Matlab для перевода из 10 в 2 систему счисления применяется функция dec2bin, которую удобно использовать в этом случае.

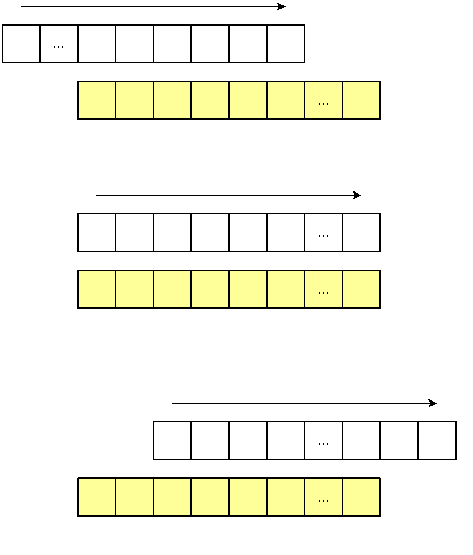
Рис. 2. Схема вычисления свертки (затемненная последовательность неподвижна)

Пик

Рис. 3. Типичные вид и свойства АКФ для М-последовательности

Для передачи в эфир каждый бит информации (“1” либо “0”) кодируется последовательностью либо . Допустим, что в эфир передается посылка Msg=[ 1 0 1 1 1 1 0 0 0 1 1 ] (11 бит), используется M-последовательность длиной 255 символов ={–1,+1,+1,–1,…}, ={+1,–1,–1,+1,…}. Тогда длина выдаваемой в эфир последовательности равна 11 х 255  = 2805 символов.

Формирование посылки в среде Matlab может быть осуществлено с помощью функции конкатенации а = [ b ; c], результатом работы которой будет вектор a, слитый из векторов b и c.

Для моделирования обработки сигнала в приемном устройстве необходимо свернуть последовательность (из 2805 символов для рассматриваемого примера) с последовательностью (из 255 символов для рассматриваемого примера). На рис. 4 положительный пик соответствует принятому биту «1» и отрицательный пик – биту «0».

Рис. 4. Типичный вид принятого сигнала после свертки

При относительной простоте генерации линейные рекуррентные кодовые последовательности имеют низкую структурную скрытность. В соответствии с соотношением (1) для формирования М-последовательности нужно знать коэффициентов . Их можно определить из уравнений вида (1) относительно неизвестных и .

Лучшей структурной скрытностью обладают нелинейные кодовые последовательности:

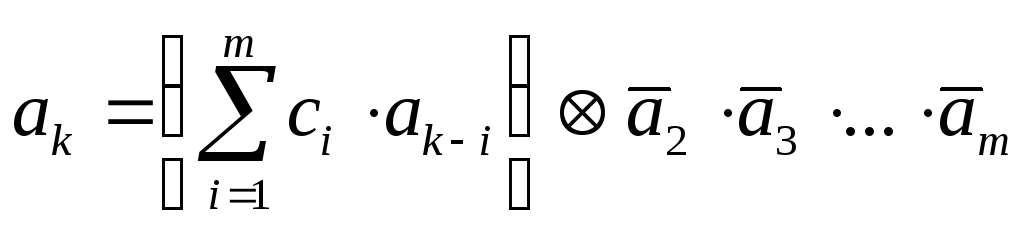, (2)

Наличие дополнительного члена, образующего нелинейную обратную связь, позволяет исключить зацикливание в связи с выработкой комбинации 00...000.

Схема формирования последовательности согласно выражению (2) приведена на рис. 5.

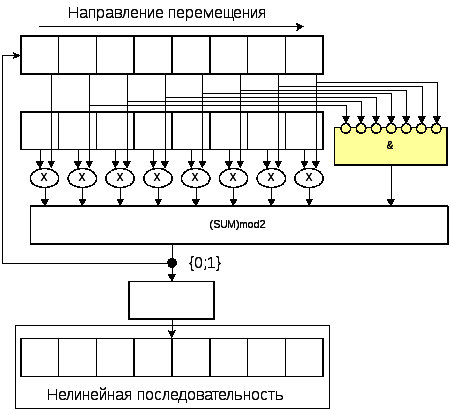
Рис. 5. Схема формирования нелинейной последовательности

Для зондирования местности и объектов с целью восприятия в радиолокационном диапазоне волн применяют внутриимпульсную модуляцию. Одним их распространенных способов является линейно-частотное модулирование (ЛЧМ).

При этом комплексный сигнал

, (3)

где a(t)=1, f₀=0, T=1, t= -0.5:0.001:0.5 после излучения также подвергается операции свертки (сжатию) в приемном тракте. Действительная и мнимая составляющие ЛЧМ-сигнала приведены на рис. 6.

Для свертки (обозначение: * ) комплексных сигналов во временной области необходимо вычислить 4 свертки действительных сигналов. Пусть – принимаемый сигнал, – сигнал в приемнике. Тогда:

. (4)

Для сигнала : re=real( u(t) ), im= – imag( u(t) ), для сигнала : re=real( u(t) ), im=imag( u(t) ). Различие заключается в знаке перед мнимыми частями.

В качестве примера на рис. 7 приведен результат свертки ЛЧМ-сигнала. Отчетливо виден пик, по которому обнаруживается принятый ЛЧМ-сигнал.

Рис. 6. Комплексные (Re, Im) составляющие ЛЧМ-сигнала

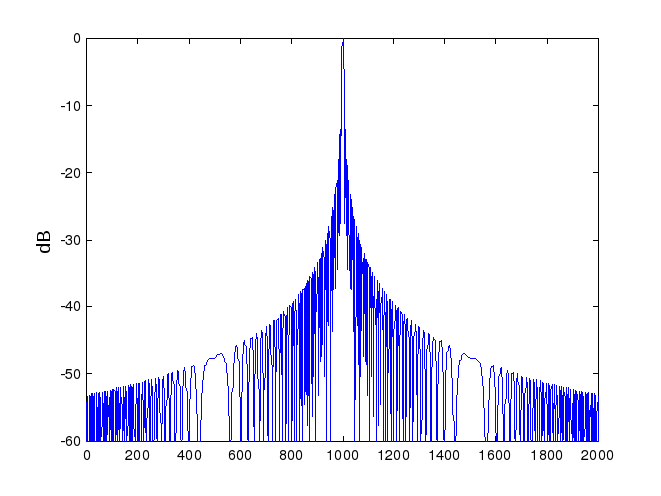
Рис. 7. Вид ЛЧМ-сигнала после свертки (сжатия)

Спектр ЛЧМ-сигнала может быть вычислен с помощью функции среды Matlab psd. В соответствии со сложившимся представлением в литературе спектр приведен на рис. 8.

Для вывода нескольких кривых на один график в среде Matlab можно использовать режимы hold on, hold off.

Рис. 8. Спектры ЛЧМ-сигнала при девиации частоты F=50…150

ЗАДАНИЕ

1. Сформируйте М-последовательность при заданных и . Постройте ее график.

2. Вычислите и постройте график АКФ полученной М-последовательности. Вычисление свертки выполнить в собственном цикле без использования функции conv. Убедитесь, что свернутая последовательность имеет один ярко выраженный пик.

3. Задайтесь кодом посылки, закодируйте ее с помощью М-последовательности. Осуществите ее передачу и декодирование. Убедитесь в правильности декодированных данных.

4. Промоделируйте наличие шума в канале связи путем его добавления к передаваемой информации (используйте функцию MATLAB normrnd, длина шумовой последовательности должна совпадать с длиной передаваемой последовательности). Сравните графики при отсутствии шума, с шумом sigma=0,5…3.

5. *Промоделируйте перехват и декодирование информации в посылке с использованием М-последовательности.

6. Найдите все характеристические многочлены М-последовательности для .

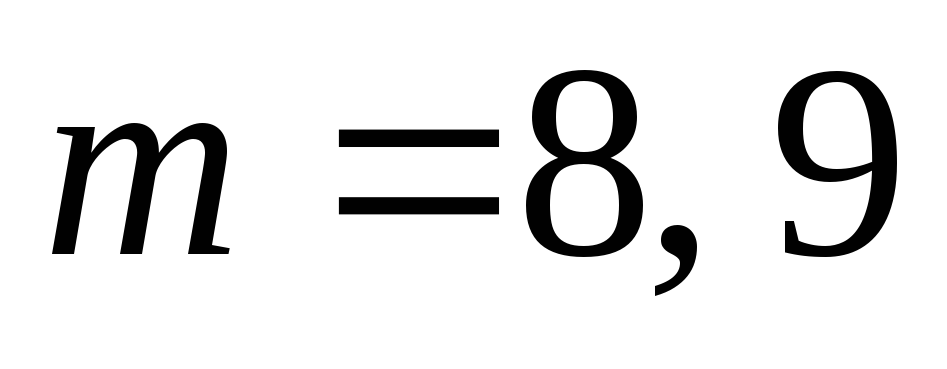7. Найдите все характеристические многочлены нелинейной последовательности для .

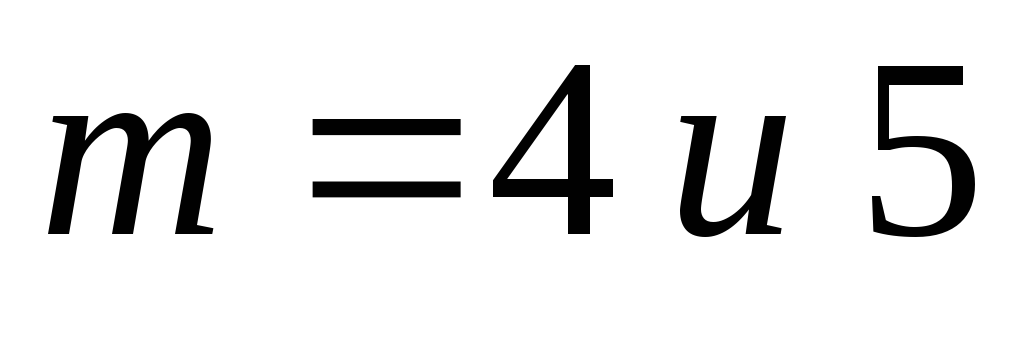8. Постройте графики ЛЧМ-сигнала, сверните его и получите спектр сигнала. Постройте графики сжатого сигнала в прямоугольных и полярных координатах. Проанализируйте зависимость спектра сигнала от формы исходных сигналов (F=20…300).

9. *Откройте пример из Demo: Toolboxes, Signal Processing, Spectral Analysis of DTMF. Пример иллюстрирует работу тонового сигнала кнопочных телефонов. Убедитесь, что спектры используемых сигналов различны. Откройте файл c:\MATLABR11\toolbox\signal\sigdemos\phone.m. По аналогии с ним рассчитайте и отобразите шкалу частот на графике спектра в задании 8.

ОТЧЕТНОСТЬ

По факту защиты лабораторной работы выставляется зачет с оценкой. Срок защиты работы – во второй половине текущей или в начале следующей лабораторной работы. При несоблюдении сроков оценка снижается на 1-2 балла.

Для защиты необходимо:

• предъявить аккуратно оформленный и отформатированный отчет в электронном виде (*.rtf, *.doc), содержащий:

– титульный лист;

– требуемые в задании ответы на теоретические вопросы;

– результаты лабораторного моделирования с соответствующими математическими выражениями, пояснениями и графическими зависимостями;

– выводы по лабораторной работе.

• ответить на вопросы по теме лабораторной работы.

ЛИТЕРАТУРА

1. Демин В.П., Куприянов А.И., Сахаров А.В. Радиоэлектронная разведка и радиомаскировка. М.: Изд-во МАИ, 1997. – 156 с.

2. Проксис Джон. Цифровая связь. Пер. с англ. ­– М.: Радио и связь, 2000. – 800 с.