5.4 Визначення та умови реалізації криптосистеми направленого шифрування

Імовірно стійкі криптосистеми шифрування називають шифрами з направленим шифруванням. Основною особливістю направлених шифрів є те, що ключ зашифрування К_з не співпадає (не повинен співпадати) з ключем розшифруваннятобто

(1.36)

В загальному випадку можна говорити що ключ прямого перетворення не повинен співпадати з ключем зворотного перетворення, тобто

(1.37)

В асиметричні криптосистемі один із ключів асиметричної пари є таємним(особистим), а інший відкритим.

Вважається , що для реалізації ймовірно – стійких криптосистем( шифрів) повинні виконуватись такі умови.

1. Шифрування( зашифрування, розшифрування ) здійснюється на основі асиметричного алгоритму та використання асиметричної пари ключів.

2. Асиметрична пара ключів складається, як мінімум, з особистого К _о, ( таємного) та відкритого К_в ключів.

3. Направлене зашифрування здійснюється з використанням відкритого ключа К_в.

4. Розшифрування використовується з використанням особистого ключа.

5. Особистий та відкритий ключі є взаємозалежними і існують алгоритми визначення одного із ключів по відомому іншому.

Інформаційні структури , що використовують асиметричні крипто перетворення отримали назву інфраструктур відкритого ключа[ 5,6,12, 31]. Вони мають достатньо значиму історію розроблення, створення та розвитку. Перші роботи в цьому напрямку стали актуальними після винаходу асиметричних криптографічних перетворень. Розроблено значне число асиметричних криптографічних систем. Їх принциповою особливістю є те, що при виконанні криптографічних перетворень в них використовується одна або декілька асиметричних пар ключів[4 – 6, 11- 13]. Нині також розглядаються ряд перспективних напрямів, що пов’язані перш за все із застосуванням криптографічних перетворень на ідентифікаторах зі спарюванням точок еліптичних кривих і на гіпереліптичних кривих. Можливість та умови застосування вказаних перетворень вивчені теоретично, створені та випробовуються дослідні версії, розроблено рекомендації та обговорюється необхідність створення регіональних і міжнародних стандартів. Буквально в 2010 році значну дорогу пробили собі криптографічні перетворення типу шифрування , що ґрунтуються на перетвореннях в урізаних кільцях поліномів, які знайшли своє закріплення в стандарті ANSI США Х 9.98 [163 - 167].

В таблиці 1 наведені дані відносно шифрів направленого шифрування.

Таблиця 1 - Асиметричні криптографічні перетворення для реалізації направленого шифрування.

Параметри НШ/ Математичний апарат	Особистий ключ НРШ	Відкритий ключ НЗШ (сертифікат)	Асиметрична пара (ключ)	Загальні параметри крипто перетворення	Сертифікати	Складність крипто аналізу
НШ в кільці (RSA)	Di	Ei	(Di , Ei)	N = P Q	Еi	Субекспоненційна
НШ в полі ГалуаF(P)	Хi	Yi=gXi(mod P)	(Xi, Yi)	P, q, g	Yi	Субекспоненційна
НШ в групі точок еліптичних кривих Е(F(q))	di	Qi=diG(modq)	(di, Qi)	a, b, G, n, f(x)(P), h	Qi	Експоненційна
НШ в гіпереліптичних кривих	Сi	D2= ciD1	(ci, D2)	f(x), g(x), q, D1, g, J	D2	Експоненційна
НШ зі спарюванням точок еліптичних кривих	diD =s QiD	QiD=H1(ID)	(diD, QiD)	G1, G2, e, H1, P, H2, H3, F2m, Pp	QiD	Експоненційна – субекспоненційна
НШ в кільці зрізаних поліномів (NTRU)	f = 1+pF(modq)	h=f 1*g*p(modq)	(f,h)	N, q, p, f, g,df, dg, c		Експоненційна – субекспоненційна

Як випливає з таблиці 1, в якості (сертифіката) відкритого ключа направленого шифрування в RSA системі використовується відкритий Ei ключ із* асиметричної пари ключа (Di, Ei), а в якості особистого ( таємного ) ключ Di. Для асиметричного криптографічного перетворення в полі Галуа як (сертифікат) відкритого ключа направленого шифрування використовується елемент поля Yi, а як особистий ключ – ціле число Хi.Для асиметричного криптографічного перетворення в групі точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується точка еліптичної кривої Qi, а як особистий ключ електронного цифрового підпису – ціле число di. При застосуванні криптографічного перетворення на гіпереліптичних кривих як сертифікат відкритого ключа використовується якобіан D2, а як особистий ключ – якобіан D1. При застосуванні криптографічного перетворення зі спарюванням точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується ключ Q_iD, а як особистий ключ – d_iD. Особливий інтерес нині мають ІВК, що ґрунтуються на криптографічних перетвореннях в кільці урізаних поліномів[6 -7 ]. Основною перевагою цього алгоритму є те, що він працює набагато швидше звичайних алгоритмів направленого шифрування з відкритим ключем, наприклад таких як RSA. Перевага у швидкості є особливо великою в генерації ключів, яке найчастіше є найбільш важливою частиною у криптографії з відкритим ключем. Для ЕЦП пряме перетворення виконується на особистому ключі, а зворотне на відкритому.

Для асиметричного криптографічного перетворення в групі точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується точка еліптичної кривої Qi, а як особистий ключ електронного цифрового підпису – ціле число di. При застосуванні криптографічного перетворення на гіпереліптичних кривих як сертифікат відкритого ключа використовується якобіан D2, а як особистий ключ – якобіан D1. При застосуванні криптографічного перетворення зі спарюванням точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується ключ Q_iD, а як особистий ключ – d_iD.

Особливий інтерес нині мають ІВК, що ґрунтуються на криптографічних перетвореннях в кільці урізаних поліномів[165 ]. Основною перевагою цього алгоритму є те, що він працює набагато швидше звичайних алгоритмів направленого шифрування з відкритим ключем, наприклад таких як RSA. Перевага у швидкості є особливо великою в генерації ключів, яке найчастіше є найбільш важливою частиною у криптографії з відкритим ключем.

5.5 Відстань єдності для безумовно стійкого шифру.

Знайти відстань єдності l₀ для безумовно стійкого шифру. В результаті маємо

.

Враховуючи, що

та ,

маємо

, (1.38)

коли та

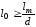(1.39)

коли .

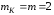Таким чином, для безумовно стійкої системи l₀ не менше довжини повідомлення, і не менше довжини ключа, оскільки d<1. Тому для успішного крипто аналізу крипто аналітик повинен отримати не менш ніж lк символів, тобто весь ключ.

Можна показати, що іншою умовою забезпечення безумовної стійкості є:

.

Покладемо, що , тоді

, (1.40)

, (1.41)

де Nk – кількість ключів, NM – кількість повідомлень.

Імовірності появи Кі ключа і Мі повідомлення є

,

,

тому

,

,

. (1.42)

В результаті отримаємо

. (1.43)

Додаток А Відстань єдності для обчислювально стійкого шифру

Приклад А. 1. Знайти l₀ для реального повідомлення (мова українська), за умови, що джерело ключів містить:

, d=0,4.

В результаті маємо

,

біт.

Приклад А.2. Визначити кількість символів ключа (обсяг ключів), які потрібно розіслати користувачам К1 і К2, зв'язаних між собою каналом зі швидкістю V=10Мг біт/с, якщо вони працюють протягом року безупинно, а на носій інформації записується 5*10⁹ бітів.

Довжина повідомлення

.

Число дисків, на які можна записати 5*109 інформації

.

Висновок: на цьому прикладі ми переконуємося, що хоча безумовно стійку систему теоретично реалізувати нескладно, проблемним є генерування та доставка великої кількості символів ключа (одноразової гами) одночасно користувачам.

Необхідно зазначити, що в безумовно стійкій крипто системі безумовна стійкість забезпечується при умові практичної відсутності колізій при формуванні ключів.