4.4 Умови реалізації обчислювальної та ймовірної стійкості крипто перетворень

4.4.1 Умови здійснення крипто аналізу

В цьому підрозділі уточнимо умови проведення крипто аналізу та розглянемо умови реалізації обчислювально та ймовірно – стійких крипто систем (перетворень)[11, 13]. При цьому розгляд будемо вести з точки зору забезпечення конфіденційності, тобто умови реалізації та загальні підходи до побудови шифрів – симетричних та асиметричних.

При розгляді шифрів будемо вважати, що порушник (крипто аналітик) має необмежений доступ до каналів телекомунікаційних систем та у випадку рис.2.3 і до носіїв інформації.

Нагадаємо, що завданням крипто аналізу є відновлення відкритого тексту без знання ключа або частини ключа, а також визначення самого ключа. Кожну спробу здійснення крипто аналізу називають атакою.

Фундаментальне припущення відносно крипто аналізу вперше було висловлено ще в 19 столітті датчанином А. Керкхоффсом, яке полягає в тому, що таємність інформації( повідомлення ), що зашифровується в повній мірі повинна залежати тільки від ключа. Інакше, стійкість криптограми ґрунтується на конфіденційності ключа. При цьому Керкхоффс виходив із допущення, що крипто аналітик має всю необхідну інформацію відносно опису криптографічної системи та засобів її реалізації. Якраз в цих умовах повинне забезпечуватись задекларований рівень криптографічно стійкості. Якщо крипто аналітик не в змозі здійснити успішно крипто аналіз в умовах повних знань, то зрозуміло, що в умовах апріорної невизначеності тим паче він не зможе успішно здійснити атаку.

При розгляді умов проведення крипто аналізу вважається, що крипто аналітик може проводити сім типів крипто аналітичних атак. При цьому для кожної із атак вважається, що крипто аналітик повністю знає криптосистему та з високою ймовірністю має доступ до криптограм. Для введеної на рис. 2.2 існують такі атаки.

1) Атака при відомому шифр тексті. При здійсненні такої атаки вважається що крипто аналітик знає все про криптосистему, має засоби її реалізації( зашифрування, розшифрування, управління ключа та має доступ до криптограм. Його задачами є дешифрування якомога більшого числа криптограм, тобто отримання відкритих текстів, А а також найкраще ще розкрити (визначити) таємний ключ. В цих умовах він зможе розшифрувати усі повідомлення(інформацію), які були зашифрована на зкомпрметованому ним ключі з використанням алгоритму Е _к. Таким чином, атака проводиться в таких умовах.

Задано:

С₁ = Е _к( М₁), С₂ = Е _к( М₂), …, С_i = Е _к( М_i). (2.55)

Необхідно визначити : повідомлення М_1, М_2….., М_i , а краще ключ К, а значить алгоритм визначення

М_i+1 із С_i+1 = Е _к( М_i+1). (2.56)

2)Атака на основ відомого відкритого тексу та відповідних йому шифр текстів. Вважається, що крипто аналітик додатково має доступ до деякого числа шифро текстів та відповідних їм відкритим текстам. Задача крипто аналітика визначити( розкрити) ключ ( або ключі), які були застосовані при за шифрування вказаних повідомлень. Визначені ключі крипто аналітик може використати для дешифрування інших шифро текстів, які отримані з застосуванням цього ключа( цих ключів). Тобто атака проводиться в таких умовах.

Задано:

М_1, С₁ = Е _к( М₁); М_2, С₂ = Е _к( М₂); …, М_i , С_i = Е _к( М_i). (2.57)

Необхідно визначити : ключ К чи алгоритм визначення

М_i+1 із С_i+1 = Е _к( М_i+1) (2.58)

3)Атака на основі підібраного відкритого тексу. При здійсненні цієї атаки, крім даних для атаки на основі відкритого шифр тексту та шифр текстів , крипто аналітик може вибирати відповідним чином відкриті тексти та здійснювати їх зашифрування, зрозуміло маючи засіб зашифрування з невідомим йому ключем. Задача крипто аналітика визначити( розкрити) ключ ( або ключі), які були застосовані при за шифрування вказаних повідомлень. Визначені ключі крипто аналітик може використати для дешифрування інших шифро текстів, які отримані з застосуванням цього ключа( цих ключів). Атака проводиться таким чином.

Задано:

М_1, С₁ = Е _к( М₁); М_2, С₂ = Е _к( М₂); …, М_i , С_i = Е _к( М_i), (2.59)

причому крипто аналітик може вибирати М_1,, . М_{2, …,} М_i .

Необхідно визначити : ключ К чи алгоритм визначення

М_i+1 із С_i+1 = Е _к( М_i+1) (2.60).

4)Атака на основі адаптивно підібраного відкритого тексу. Ця атака носить особливий характер, вона виконується з використанням спеціально підібраного тексту(текстів), а також при знанні даних для атаки на основі підібраного тексту. В подальшому крипто аналітик може уточнювати вибір наступного тексту в залежності від отриманих попередніх результатів, в тому числі вибирати блоки меншої довжини. Визначений ключ (ключі) крипто аналітик може використати для дешифрування інших шифро текстів, які отримані з застосуванням цього ключа( цих ключів). В цьому випадку атака проводиться таким чином.

Задано:

М_1, С₁ = Е _к( М₁); М_2, С₂ = Е _к( М₂); …, М_i , С_i = Е _к( М_i), (2.61)

причому крипто аналітик може вибирати М_1,, . М_{2, …,} М_i .

Мається доступ до М_1, С₁ = Е _к( М₁); На основі отриманих даних вибирається М_2, С₂ = Е _к( М₂); …, На основі отриманих даних вибирається М_i , С_i = Е _к( М_i).

Необхідно визначити ключ К чи алгоритм визначення

М_i+1 із С_i+1 = Е _к( М_i+1) (2.62).

5)Атака на основі підібраного шифро тексу. При здійсненні цієї атаки крипто аналітик може вибирати шифро тексти С_i = Е _к( М_i) та використовуючи засіб з введеним в нього ключем К, розшифровувати вибрані шифро тексти, тобто отримувати М_i . Особливість цієї атаки в тому, що крипто аналітик має засіб розшифрування з введеним в нього ключем, але ключ йому не доступний ніяким чином. Визначений ключ ( ключі) крипто аналітик може використати для дешифрування інших шифро текстів, які отримані з застосуванням цього ключа( цих ключів). В даному випадку атака проводиться таким чином.

Задано:

С_1, М₁ = D _к( C₁); C_2, M ₂ = D _к( C₂); …, C_i , M_i = D _к( М_i), (2.63)

причому крипто аналітик може вибирати D _1, . D_{2, …,} D _i .

Необхідно визначити : ключ К, що міститься в засобі в недоступній формі.

Розглянута атака в основному може бути застосованою відносно криптосистем з відкритим ключем., а також за деякими обмеженнями і відносно симетричних криптосистем.

6) Атака на основі підібраного ключа. В цьому випадку ключ може підбиратись, якщо він зв’язаний з іншими ключами, вибирається з обмеженої множини, має певні відомі крипто аналітику властивості або генерується засобами, що мають погані властивості нерозрізнюваності та корельовані між собою тощо. Прикладом можуть бути зв’язані між собою таємні ( особисті) ключі[ ], циклові ключі блокових симетричних шифрів тощо.

7) Грабіжницький «аналіз». В цьому випадку ключ( ключі) отримуються на основі використання агентури, шантажу власників ключів, їх підкупу, застосування торту тощо. Враховуючи велику обчислювальну складність атак 1) -6) метод грабіжницького аналізу найбільш ефективний та реальний.

4.4.2 Визначення обчислювально стійкої криптосистеми та умови реалізації

Згідно ( 2.17) під обчислювально стійкими криптосистеми (шифрами) будемо вважати такі, відносно яких складність крипто аналізу носить експоненційний характер і значення безпечного часу на багато більше часу цінності інформації, тобто

В ряді випадків обчислювально стійкі криптосистеми( шифри) називають шифрами з гарантованою крипто стійкістю. Прикладами таких шифрів є блокові та потокові симетричні шифри. Розглянемо умови реалізації обчислювально стійкої криптосистеми на прикладі застосування симетричних шифрів. У обчислювально стійких криптосистемах замість ключової послідовності К i, що використовується в безумовно стійких шифрах, використовують спеціальним чином генеровану гаму шифрування Гi. Правило зашифрування зводиться ло складання символів повідомлення та гами зашифрування за певним модулем m та має вигляд

(2.64)

, (2.65)

D (2.65) - вихідний (початковий, робочий, діючий) ключ, агама шифрування генерується у відповідності з цим ключем та діючими параметрамишифру (блочного чи поточного).

Розшифровування шифротексту здійснюється за правилом

(2.66)

Основними умовами забезпечення обчислювальної стійкі є такі [ 2, 4 - 7 ].

1. Гама повинна генеруватись спеціальними засобами – генераторами гами .

2. Символи гами повинні генеруватись випадково, рівно ймовірно, незалежно та одно рідно.

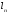3. Період повторення гами повинен бути не менше допустимої величиниl_д, тобто

(2.67)

4. Закон формування гами повинен забезпечувати „ секретність ” гами, тобто непередбачуваність . Цю вимогу можна звести до вимоги, що складність обернення рівняння (2.65), тобто знаходження ключа

(2.68)

повинна носити експоненційний характер.

Відмітимо Що в якості показника оцінки складності гами можна використовувати поняття її структурної скритності, наприклад у вигляді

, (2.69)

де l _н число символів гами, які потрібно знати для розкриття тих що залишились, тобто l_п - l_н. При цьому найкращою буде гама , для якої, а значить на основі (2.69) S_c 1.

5. Відновлюваність гами в просторі та часі, тобто наявності можливості генерувати ідентичні гами на різних станціях та в різний час.

6. Забезпечення допустимого рівня появи колізій, тобто ідентичних відрізків гами.

7. Допустима складність (швидкодія) генерування гами в просторі та часі тощо

Необхідно відмітити, що у більшості випадків здійснюють двійкове шифрування, тобто за модулем 2. За даних умов правила шифрування (2.64) та (2.65) мають такий вигляд

, (2.70)

. (2.71)

Для оцінки стійкості обчислювально стійкої криптосистеми можна використовувати показники, що введені в ( 2.4.2) кортеж параметрів (2.15) - ( N _k , H(К) , , γ, Р _у, l₀ )

4.4.3 Визначення та умови реалізації ймовірно стійкої криптосистеми (шифру)

Імовірно стійкі криптосистеми шифрування називають шифрами з направленим шифруванням. Основною особливістю направлених шифрів є те, що ключ зашифрування К_з не співпадає (не повинен співпадати) з ключем розшифруваннятобто

(2.72)

В загальному випадку можна говорити що ключ прямого перетворення не повинен співпадати з ключем зворотного перетворення, тобто

(2.73)

В асиметричні криптосистемі один із ключів асиметричної пари є таємним(особистим), а інший відкритим.

Вважається , що для реалізації ймовірно – стійких криптосистем( шифрів) повинні виконуватись такі умови.

1. Шифрування( зашифрування, розшифрування ) здійснюється на основі асиметричного алгоритму та використання асиметричної пари ключів.

2. Асиметрична пара ключів складається, як мінімум, з особистого К _о, ( таємного) та відкритого К_в ключів.

3. Направлене зашифрування здійснюється з використанням відкритого ключа К_в.

4. Розшифрування використовується з використанням особистого ключа.

5. Особистий та відкритий ключі є взаємозалежними і існують алгоритми визначення одного із ключів по відомому іншому.

6. При реалізації асиметричного шифрування повинні застосовуватись загальні параметри криптографічних перетворень , але такі що складність відомих атак повинна мати не нижче за суб експоненційну.

7. Асиметричне криптографічне перетворення повинне дозволяти реалізацію моделі взаємної недовіри та взаємного захисту.

8. Асиметрична ключова пара, як правило, повинна генеруватись власником цієї пари ключів.

9. Усі алгоритми та засоби криптографічних перетворень повинні забезпечувати цілісність та справжність загальних параметрів та ключів.

Інформаційні структури , що використовують асиметричні крипто перетворення отримали назву інфраструктур відкритого ключа[ 5,6,12, 31]. Вони мають достатньо значиму історію розроблення, створення та розвитку. Перші роботи в цьому напрямку стали актуальними після винаходу асиметричних криптографічних перетворень. Розроблено значне число асиметричних криптографічних систем. Їх принциповою особливістю є те, що при виконанні криптографічних перетворень в них використовується одна або декілька асиметричних пар ключів[4 – 6, 11- 13]. Нині також розглядаються ряд перспективних напрямів, що пов’язані перш за все із застосуванням криптографічних перетворень на ідентифікаторах зі спарюванням точок еліптичних кривих і на гіпереліптичних кривих. Можливість та умови застосування вказаних перетворень вивчені теоретично, створені та випробовуються дослідні версії, розроблено рекомендації та обговорюється необхідність створення регіональних і міжнародних стандартів. Буквально в 2010 році значну дорогу пробили собі криптографічні перетворення типу шифрування , що ґрунтуються на перетвореннях в урізаних кільцях поліномів, які знайшли своє закріплення в стандарті ANSI США Х 9.98 [163 - 167]. У таблиці 1 наведено основні асиметричні крипто перетворення, що застосовуються або можуть застосовуватись для таких криптографічних перетворень як направлене шифрування, як (електронний) цифровий підпис, узгодження ключів тощо . Як випливає з таблиці 2.2, в якості (сертифіката) відкритого ключа направленого шифрування в RSA системі використовується відкритий Ei ключ із* асиметричної пари ключа (Di, Ei), а в якості особистого ( таємного ) ключ Di.

Для асиметричного криптографічного перетворення в полі Галуа як (сертифікат) відкритого ключа направленого шифрування використовується елемент поля Yi, а як особистий ключ – ціле число Хi.

Таблиця 2.2

Асиметричні криптографічні перетворення для ЕЦП

Параметри перетворення / Вид перетворення	Особи стий ключ	Відкритий ключ (сертифікат)	Асиметрична пара (ключ)	Загальні параметри	Сертифікати	Складність крипто аналізу
Перетворення в кільці (RSA)	Di	Ei	(Ei, Di)	N = PQ	Ei	Субекспоненційна
Перетворення в полі Галуа F(P) (DSA)	Хi	Yi= gXi(mod P)	(Xi, Yi)	P, q, g	Yi	Субекспоненційна
Перетворення в групі точок еліптичних кривих Е(F(q))	di	Qi= diG(modq)	(di, Qi)	a, b, G, n, f(x)(P), h	Qi	Експоненційна
Перетворення в гіпереліптичних кривих	Сi	D2= ciD1	(ci, D2)	f(x), g(x), q, D1, g, J	D2	Експоненційна
Перетворення зі спарюванням точок еліптичних кривих	Di = s QiD	QiD = H1(ID)	(diD, QiD)	G1, G2, e, H1, P, H2, H3, F2m, Pp	QiD	Міжекспоненційна – субекспоненційна

Для асиметричного криптографічного перетворення в групі точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується точка еліптичної кривої Qi, а як особистий ключ електронного цифрового підпису – ціле число di. При застосуванні криптографічного перетворення на гіпереліптичних кривих як сертифікат відкритого ключа використовується якобіан D2, а як особистий ключ – якобіан D1. При застосуванні криптографічного перетворення зі спарюванням точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується ключ Q_iD, а як особистий ключ – d_iD.

Особливий інтерес нині мають ІВК, що ґрунтуються на криптографічних перетвореннях в кільці урізаних поліномів[165 ]. Основною перевагою цього алгоритму є те, що він працює набагато швидше звичайних алгоритмів направленого шифрування з відкритим ключем, наприклад таких як RSA. Перевага у швидкості є особливо великою в генерації ключів, яке найчастіше є найбільш важливою частиною у криптографії з відкритим ключем.

Детально класифікація та математичні моделі асиметричних крипто перетворень, що подані в таблиці наведені в 3 розділі монографії.

Додаток А

4.3.3 Приклади розв’язку задач оцінки стійкості

Приклад 1. Знайти l0 для безумовно стійкого шифру. В результаті маємо

.

Враховуючи, що

та ,

маємо

, (2.43)

коли та

(2.44)

коли .

Таким чином, для безумовно стійкої системи l0 не менше довжини повідомлення, і не менше довжини ключа, оскільки d<1. Тому для успішного крипто аналізу крипто аналітик повинен отримати не менш ніж lк символів, тобто весь ключ.

Можна показати, що іншою умовою забезпечення безумовної стійкості є:

.

Покладемо, що 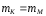, тоді

, (2.45)

, (2.46)

де Nk – кількість ключів, NM – кількість повідомлень.

Імовірності появи Кі ключа і Мі повідомлення є

,

,

тому

,

,

. (2.47)

В результаті отримаємо

. (2.48)

Приклад 2. Знайти l₀ для реального повідомлення (мова українська), за умови, що джерело ключів містить:

, d=0,4.

В результаті маємо

,

біт.

Приклад 3. Знайти l₀ для безумовно стійкого шифру. В результаті маємо

.

Враховуючи, що

та ,

маємо

, (2.49)

коли та

(2.50)

коли .

Таким чином, для безумовно стійкої системи l₀ не менше довжини повідомлення, і не менше довжини ключа, оскільки d<1. Тому для успішного крипто аналізу крипто аналітик повинен отримати не менш ніж lк символів, тобто весь ключ.

Можна показати, що іншою умовою забезпечення безумовної стійкості є:

.

Покладемо, що , тоді

, (2.51)

, (2.52)

де N_k – кількість ключів, N_M – кількість повідомлень.

Імовірності появи Кі ключа і Мі повідомлення є

,

,

тому

,

,

. (2.53)

В результаті отримаємо

. (2.54)

Приклад 4. Визначити кількість символів ключа (обсяг ключів), які потрібно розіслати користувачам К1 і К2, зв'язаних між собою каналом зі швидкістю V=2Мг біт/с, якщо вони працюють протягом року безупинно, а на носій інформації записується 5*10⁹ бітів.

Довжина повідомлення

.

Число дисків, на які можна записати 5*109 інформації

.

Висновок: на цьому прикладі ми переконуємося, що хоча безумовно стійку систему теоретично реалізувати нескладно, проблемним є генерування та доставка великої кількості символів ключа (одноразової гами) одночасно користувачам.

Необхідно зазначити, що в безумовно стійкій крипто системі безумовна стійкість забезпечується при умові практичної відсутності колізій при формуванні ключів.