4.3 Умови та приклади реалізації криптосистем з безумовним рівнем стійкості

В цьому розділі,притримуючись формалізованого підходу, розглянемо загальні умови та вимоги відносно побудування криптосистем з безумовною, обчислювальною (гарантованою), ймовірно стійкою та обчислювально нестійкою стійкістю криптосистеми.

Розгляд та умови реалізації розпочнемо криптосистем розпочнемо у відповідності з рівнями гарантій стійкості.

4.3.1 Умови реалізації безумовно стійких криптосистем.

Визначення умов реалізації криптосистем безумовної стійкості є непростим та неоднозначним. Але на формальному рівні їх можна визначити, висунувши вимоги до практичної реалізації. В [1 ] на достатньо формальному рівні визначені необхідні та достатні умови забезпечення безумовної стійкості. Для захисту особливо критичної інформації в частині забезпечення високого рівня конфіденційності можуть використовуватися криптографічні перетворення, що забезпечують безумовну стійкість .

Теорема 2.5.1 Необхідною і достатньою умовами забезпечення безумовної стійкості є:

, (2.20)

тобто імовірність появи Сj криптограми на виході шифратора не повинно залежати від того, яке Мі повідомлення з’явилось на виході джерела повідомлення. Інакше, ймовірність появлення криптограми повинно бути однаковою для всіх ключів і для всіх повідомлень. Це означає, що будь-яке повідомлення може зашифровуватись в будь-яку криптограму з однаковою ймовірністю.

Доведення. Визначимо апостеріорну імовірність , яку може обчислити порушник (крипто аналітик), знаючи апріорні ймовірності,та, використовуючи відому теорему теорії ймовірності та математичної статистики, в нашому випадку співвідношення (2.7)

. (2.21)

Нехай крипто аналітик знаходиться відносно ІТС в умовах згідно рис.2.2. Ясно, що він не отримає ніякої інформації відносно джерела інформації ( буде мати нульові знання), якщо

, (2.22)

Дійсно, в цьому випадку згідно (2.11)

(2.23).

Підставивши (2.22) в (2.23) отримаємо що

(2.24)

Теорему доведено для загальних умов.

4.3. 2 Приклади реалізації безумовно стійкої криптосистеми.

Криптографічні системи для яких виконується ця умова і є безумовно стійкими[1, 2,11,13]. Прикладом реалізації такої системи є система Вернама. У цій системі здійснюється потокове шифрування, тобто символи криптограми в шифраторі зашифруються за правилом:

, (2.25)

де Мi – i-й символ повідомлення , , а Кі – і-й символ ключа, Сі - i-й символ криптограми, m – розмір алфавіту, що використовується.

Відмінною рисою системи Вернама є те, що символи ключа Кi мають генеруватись(породжуватися) випадково, рівно ймовірно та незалежно. У такій системі символів ключа (довжина ключа) має бути не менше довжини повідомлення, тобто

. (2.26)

Розшифрування в системі Вернама здійснюється згідно з правилом

. (2.27)

Аналіз (2.25) і (2.27) показує, що для зашифрування і розшифрування потрібно використовувати однакову випадкову послідовність (ключ).

Можна показати, що для системи, яка розглядається, умовна ентропія 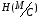[7]:

, (2.28)

де l – довжина криптограми, d – надмірність алфавіту повідомлень.

Визначимо умову, при якій реалізується безумовна стійкість, тобто знайдемо число символів криптограми, при якому не можна здійснити крипто аналіз.

Задача крипто аналізу може бути розв’язана, коли:

.

Тоді із (2.28) випливає, що

. (2.29 )

Розв’язавши рівняння (2.29) отримаємо, що відстань єдності l₀ визначається як

. (2.30)

Фізично параметр l₀ означає мінімальну кількість символів криптограми при правильному отриманні яких можна сподіватися на успішний крипто аналіз. Якщо l<l₀, то система безумовно стійка. Це друга умова реалізації безумовно стійкої системи.

Очевидно, що успіх крипто аналітика у розв’язанні задачі крипто аналізу залежить від обсягу криптограм, який він отримав. При цьому крипто аналітик знаходиться в невизначеності , причому

. (2.31)

Найкращий випадок, якщо .

Використовуючи функції ненадійності Шеннона [7]:

, (2.32)

де l – загальний обсяг символів криптограми, який необхідно перехопити для розв’язання задачі крипто аналізу, а також враховуючи, що при l₀ , можна скласти і вирішити систему лінійних рівнянь і вона матиме одне розв’язання. При цьому вирішення самої задачі може бути дуже складним, але воно є і єдине.

Для деякого класу лінійних (групових) шифрів, у яких використовуються природні мови (російська, англійська, С++, графіка) Кл. Шеннон отримав розв’язок рівняння (2.28), якщо

,

, (2.33)

(2.34)

і апостеріорна ентропія визначається через умовну апостеріорну імовірність,

то

, (2.35)

, (2.36)

.

Далі можна розрахувати за (2.35), знаючи статистики Р(Сj) і.

Надмірність d визначається залежністю символів мови між собою та різними ймовірностями появи їх в тексті. Вона може бути визначена, як

, (2.37)

де Н₀(М) – ентропія мови, де всі символи порівняно ймовірні і незалежні.

Якщо

, (2.38)

то

, (2.39)

тому

. (2.40)

Використовуючи рівняння (2.34), маємо для мови з m алфавітом

. (2.41)

Для двійкового алфавіту (m=2)

. (2.42)