
- •4.4.1Модель завадо захищеного каналу.
- •4.4.2 Поняття складеного сигналу.
- •4.4.3 Теоретичні положення про криптографічний захист на рівні складеного сигналу.
- •4.4.4 Математична модель, структурна схема динамічного радіоканалу
- •4.4.5 Методи формування Гу управляючих і ключових даних
- •Методы построения и исследования свойств производных нелинейных рекуррентных последовательностей
Методы построения и исследования свойств производных нелинейных рекуррентных последовательностей
И. Д. ГОРБЕНКО, д. т. н., А. А. ЗАМУЛА, к. т. н., Р. И. КИЯНЧУК.
Системы
нелинейных рекуррентных последовательностей
(НРП) являются плотноупакованными по
периодической функции корреляции
(ПФАК), существуют для большого спектра
длительностей L,
однако размерность ансамбля НРП
ограничена, например для НРП
характеристического типа, функцией
Эйлера. Проведенные исследования
показали, что дальнейшее увеличение
размерности ансамбля и улучшение
структурных свойств может быть достигнуто
на основе использования L-позиционных
НРП, построение которых осуществляется
посредством образования последовательного
произведения

 ,
символов
,
символов
 НРП с одно- или двухуровневой ПФАК.
НРП с одно- или двухуровневой ПФАК.
Правило
построения символов
 производных нелинейных рекуррентных
последовательностей (ПНРП) сформулируем
в виде
производных нелинейных рекуррентных
последовательностей (ПНРП) сформулируем
в виде
|
|
(1) |
ПФАК,
построенную по (1) ПНРП, найдем, используя
соотношение
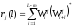 :
:
|
|
(2) |
где
в общем случае
 .
.
Анализ корреляционных свойств с использованием (2) в общем виде затруднен, поэтому рассмотрим ряд частных случаев, важных как c теоретической, так и практической точкек зрения.
1.
Пусть
 ,
а
,
а
 ,
тогда (2) имеет вид
,
тогда (2) имеет вид
|
|
(3) |
Для
преобразования (3) представим индекс
суммирование i
в
 -р
ичной системе счисления
-р
ичной системе счисления
|
|
(4) |
|
|
(5) |
С
учетом, того, что

|
|
(6) |
Кроме
того, если
 принимает значение из множества вычетов
по
принимает значение из множества вычетов
по
 то
то
 пробегает значения по модулю
пробегает значения по модулю
 ,
поэтому
,
поэтому
|
|
(7) |
и ПФАК ПНРП может быть вычислена с использованием выражения
|
|
(8) |
Но
так как
 и
и
 могут принимать соответственно значения
могут принимать соответственно значения
 и
и
 при
при

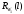 и
и
 при
при
 ,
то
,
то
|
|
(9) |
Анализ
(9) показывает, что минимальные боковые
лепестки ПНРП достигаются в случае,
если 
 ,
,
 ,
,
 ,
,
 принимают
минимальные значения. Кроме того, как
следуает из [1] ПНРП имеет максимальный
период, если
принимают
минимальные значения. Кроме того, как
следуает из [1] ПНРП имеет максимальный
период, если
 и
и
 взаимно простые числа.
взаимно простые числа.
2.
Пусть 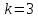
 ,
а
,
а
 .
В этом случае по аналогии с (9) выражение
(2) можно представить в виде
.
В этом случае по аналогии с (9) выражение
(2) можно представить в виде
|
|
(10) |
Или
|
|
(11)
|
Рассмотрение
(11) показывает, что для минимизации
 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
 ,
,

 и
и 
 были минимальными, а
были минимальными, а
 ,
,
 и
и
 – минимальными и взаимопростыми.
Минимальное значение
– минимальными и взаимопростыми.
Минимальное значение ,
,
 ,
равное 0 и достигается только при
использовании в качестве
,
равное 0 и достигается только при
использовании в качестве
 последовательности [2] вида {1 1 1 -1}. В этом
случае выражение (11) принимает вид
последовательности [2] вида {1 1 1 -1}. В этом
случае выражение (11) принимает вид
|
|
а) б) в) г) |
(12) |
Исследование
выражений (12 а,
б
и г)
показывает, что для их минимизации
необходимо, чтобы как принимаемые
значения ПФАК ,
,

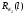 и
и 
 ,
так и значения их длительностей были
бы минимальными. С учетом того, что
,
так и значения их длительностей были
бы минимальными. С учетом того, что 
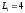 ,
максимальные значения ПФАК
,
максимальные значения ПФАК 
 дают слагаемые в)
и г).
Если
дают слагаемые в)
и г).
Если 
 и
и
 – взаимнопростые, то минимальные
значения
– взаимнопростые, то минимальные
значения
 и
и 
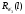 могут быть соответсвенно равны
могут быть соответсвенно равны 
 и
и
 или
или 
 ,
или
,
или 
 ,
поэтому
,
поэтому
|
|
а) б) в) г) |
(13) |
Если

 и
и
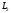 – взаимнопростые, то выражение
– взаимнопростые, то выражение

 принимает
значение либо
принимает
значение либо

 ,
либо
,
либо
 ,
поэтому максимальный боковой лепесток
дает составяющая
,
поэтому максимальный боковой лепесток
дает составяющая 
 .
.
Из
рассмотренного выше следует, что для
минимизации боковых лепестков необходимо,
чтобы
 ,
,
 и
и
 были взаимнопростыми. Этого можно
достичь, если
были взаимнопростыми. Этого можно
достичь, если
 и
и

 – простые, а
– простые, а
 .
При этих условиях составляющие (11)
принимают значения
.
При этих условиях составляющие (11)
принимают значения
|
|
(14) |
3.
Пусть 
 ,
а
,
а
 .
Для этих условий с учетом (2) выражение
для ПФАК ПНРП можно представить в виде
.
Для этих условий с учетом (2) выражение
для ПФАК ПНРП можно представить в виде
|
|
(15) |
причем
(15) позволяет вычислить ПФАК, если
положить, что 
 .
.
Проведенные исследования показали, что для (15) можно получить оценки, если воспользоваться теорией двухзначных характеров, в частности, тем, что для любого нетривиального характера справедливо [3]
 ,
,
и
фиксированными правилами кодирования.
Например, для наиболее мощного класса
двухуровневых последовательностей –
последовательностей характеристического
типа с числом символов 
 ,
,

 ;
;
|
|
а)
б) |
(16) |
где
 — q-ый
первообразный элемент поля
— q-ый
первообразный элемент поля 
 ,
а
,
а 
 – m-ый
первообразный примитивный полином
степени n.
– m-ый
первообразный примитивный полином
степени n.
Приведем вывод аналитического выражения для ПФАК ПНРП.
Используя
(15) и полагая, что 
 ,
имеем
,
имеем
|
|
(17) |
С
учетом того, что 
 ,
[4], при
,
[4], при

|
|
(18) |
где Z – учитывает сумму слагаемых, входящих в (17), для которых
|
|
(19) |
Более точно структуру (19) определяют сформулированные ниже утверждения.
Утверждение
1. Пусть и
и
 есть
элементы поля
есть
элементы поля 
 а
а
 –
–
 -ый
первообразный элемент, тогда при
-ый
первообразный элемент, тогда при

 и
и
 никогда не сравнимы с
никогда не сравнимы с
 .
Доказательство утверждения следует из
цикличности поля
.
Доказательство утверждения следует из
цикличности поля 
 [4].
[4].
Утверждение
2. Пусть
 и
и 
 – элементы поля
– элементы поля 
 ,
а
,
а
 и
и
 –
первообразные. Существуют
–
первообразные. Существуют 
 и
и 
 автоморфные преобразования, при которых
автоморфные преобразования, при которых
 .
.
Доказательство
утверждения следует из авто- и изоморфных
свойств поля
 [4].
[4].
 С учетом утверждения (17) и (18) выражение
(19) распадается на следующие логические
высказывания.
С учетом утверждения (17) и (18) выражение
(19) распадается на следующие логические
высказывания.
|
|
а) б) в) г) д) е) ж) з) |
(20) |
Анализ (20) показывает, что исключающими являются высказывания а), г), ж), з), поэтому
 ,
,
|
|
(21) |
Действительно,
если истинно высказываение (20, а), то
 ,
так как
,
так как
 [4], поэтому
[4], поэтому
 .
.
В
случае, если
 ,
то
,
то
 .
.
Преобразуем
выражение (18), используя свойство
характера 
 [Альберт], не рассматривая
[Альберт], не рассматривая
 сумму, определяемую (П. 7.5), обозначив
его переменной
сумму, определяемую (П. 7.5), обозначив
его переменной
 :
:
|
|
(22) |
Проанализируем выражение
 ,
,
учитывая,
что если
 принимает
значения индексов суммирования, то
степени первообразных элементов
принимает
значения индексов суммирования, то
степени первообразных элементов
 и
и
 принимают значения всех ненулевых
элементов поля
принимают значения всех ненулевых
элементов поля
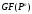 .
Обозначая ненулевые элементы поля через
.
Обозначая ненулевые элементы поля через
 и
и
 соответственно для первообразных
соответственно для первообразных
 и
и
 ,
при
,
при
 ,
перейдем к сумме произведения характеров
ненулевых элементов
,
перейдем к сумме произведения характеров
ненулевых элементов
|
|
(23) |
Полагая
в (23)
 и
и
 ,
проанализируем все
,
проанализируем все и
и
 ,
если
,
если
 и
и
 пробегают при изменении все ненулевые
элементы поля
пробегают при изменении все ненулевые
элементы поля 
 ,
то
,
то
 и
и
 так же пробегают все ненулевые поля
так же пробегают все ненулевые поля

 исключая 1, поэтому
исключая 1, поэтому
|
|
(24) |
Если же
|
|
а) б) в) |
(25) |
Исключим
в (25) условие
 ,
для этого добавим в него и вычтем
,
для этого добавим в него и вычтем
 ,
,
 и
и
 .
В результате получим
.
В результате получим
|
|
(26) |
Даже,
принимая во внимание, что
 и
и
 являются постоянными, обозначив их как
являются постоянными, обозначив их как
 и
и
 ,
,
 ,
а также обозначив
,
а также обозначив
 и
и
 ,
которые пробегают так же все элементы
поля
,
которые пробегают так же все элементы
поля 
 ,
получим
,
получим

С учетом (21), (23), (25), выражение (18) есть:
|
|
(27) |
где
запись 
 означает, что слагаемые в скобках
необходимо брать со знаками
означает, что слагаемые в скобках
необходимо брать со знаками 
 во всевозможных сочетаниях, то есть
во всевозможных сочетаниях, то есть
 -
сочетаний, если
-
сочетаний, если
 -число
слагаемых.
-число
слагаемых.
Упростим (27) учитывая, что все слагаемые
|
|
(28) |
Из
(28) непосредственно следует, что

 принимает
значение на множестве чисел
принимает
значение на множестве чисел
 .
Поэтому, используя (28), выражение (27)
можно представить
.
Поэтому, используя (28), выражение (27)
можно представить
|
|
(29) |
где
запись [3] и [4] означает, что вместо [3] при
анализе необходимо подставлять числа
 ,
а вместо [4] – числа
,
а вместо [4] – числа 
 .
.
Рассмотрим вывод аналитического выражения для ПФВК ПНРП. Используя выражение для расчета функции взаимной корреляции

получим

|
|
(30) |
Приведем вывод выражения для оценки выбросов ПФВК
|
|
(30) |
Далее, аналогично выражению (19)
|
|
(31) |
где
 представляет собой сумму слагаемых,
входящих в (30), для которых
представляет собой сумму слагаемых,
входящих в (30), для которых
 ,
что эквивалентно:
,
что эквивалентно:
|
|
а) б) в) г) |
|
поэтому:
|
|
(32) |
может
принимать значения на множестве 
 следовательно (29) есть
следовательно (29) есть
|
|
(33) |
Преобразуем
выражение для
 следующим образом:
следующим образом:
|
|
(34) |
Далее,
выражение для
 (обозначив
(обозначив
 и
и
 ),
представим в виде:
),
представим в виде:
|
|
|
С
учетом (24) – (26), а также того, что
 и
и
 могут принимать все значения из
могут принимать все значения из 
 ,
обозначив
,
обозначив
 и
и
 ,
причем , так как, во-первых,
,
причем , так как, во-первых, 
 и
и
 ,
, ,
а во-вторых, при
,
а во-вторых, при
 и
и
 ,
,
 ,
(34) можно представить в виде:
,
(34) можно представить в виде:
|
|
(35) |
Анализ
(35) показывает, что элементы полей 
 представляют собой автоморфизмы полей
представляют собой автоморфизмы полей

 и
и
 при
при
 .
Сумма в нем берется по всевозможным
произведениям характеров над
.
Сумма в нем берется по всевозможным
произведениям характеров над 
 и дает оценку для максимально достигаемого
выброса
и дает оценку для максимально достигаемого
выброса
 .
С учетом того, что элементы
.
С учетом того, что элементы
 ,
,
 ,
,
 и
и
 строятся
по различным первообразным и пары
условий
строятся
по различным первообразным и пары
условий

не истинны, (35) имеет вид
|
|
(36) |
Важной
задачей является несбалансированность
ПНРП по число символов
 и
и
 .
.
Если
 – первообразные элементы поля
– первообразные элементы поля
 ,
то несбалансированность в числе символов
есть
,
то несбалансированность в числе символов
есть

При
 аналогично (32)
аналогично (32)

где
 представляет собой сумму слагаемых,
для которых
представляет собой сумму слагаемых,
для которых
|
|
(37) |
то есть
|
|
(38) |
Далее
обозначив
 и
и
 ,
а затем
,
а затем
 и
и
 аналогично (21) –
(25) имеем
аналогично (21) –
(25) имеем
|
|
(39) |
С учетом (39)
|
|
(40) |
Заметим,
что для случая
 ,
,
 можно оценить используя соотношения
(36), то есть
можно оценить используя соотношения
(36), то есть
|
|
(41) |
Анализ
(41) показывает, что несбалансированность,
а следовательно, и шумы неортогональности
с увеличением
 увеличиваются и уже при
увеличиваются и уже при
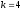 достигают значительной величины, даже
без учета результатов сумм в (40) и (41).
достигают значительной величины, даже
без учета результатов сумм в (40) и (41).
Особенности вычисления выражений (29), (36), (41) и оценки их значений рассмотрим на примере выражения (41).
Воспользовавшись свойством функции характеров, имеем
|
|
(42) |
Для случая двухзначного характера, используя (15) имеем
|
|
(43) |
Непосредственный
анализ (43) показывает, что оценка
максимальных боковых леместков ПФАК,
ПФВК и несбалансированности (то же
максимальной) в числе символов
 и
и
 может быть сведена к изучению
насбалансированности по четности и
нечетности индексов производного поля,
элементами которого являются числа
(полиномы) вида
может быть сведена к изучению
насбалансированности по четности и
нечетности индексов производного поля,
элементами которого являются числа
(полиномы) вида
 .
.
Сопоставительное
рассмотрение (43) показывает, что для
анализа НРП (ПНРП) по критерию минимума
максимальных выбросов
 с точки зрения вычислительной сложности,
предпочтительнее использовать алгоритм
(42), а при вычислении основных статистических
харктеристик алгоритм (43).
с точки зрения вычислительной сложности,
предпочтительнее использовать алгоритм
(42), а при вычислении основных статистических
харктеристик алгоритм (43).
Список литературы: 1 Виноградов И.М. Основы теории чисел. М. Наука, 1965 г. 2 Свердлик М.Б.Оптимальные дискретные сигналы. М., «Сов. Радио», 1975, 200 с. 3. Холл М. Комбинаторика. М. Мир. 1970 – 421 с. 4. Альберт А. А. Константные поля. В киберн. сб. ВМП. З. М.: Мир, 1966. – 242 с.

 .
.
 ,
, .
.
 .
.









 либо
либо

 .
.









 .
.
 .
.







 .
.

















