4.4.5 Методи формування Гу управляючих і ключових даних

Проведені дослідження показали що Гама управління

Г_у повинна володіти таким ж стандартними властивостями, як і Г_ш :

1.

2. Основа алфавіту повинна бути т - ічною.

4. використання довгострокових ключів;

5. використання ключів сеансу;

6. передачі маркерів синхронізації або управляючих послідовностей у кожній команді.

1. Сутність методу генерування ПВП на основі багатомодульних перетворень

Він дозволяє генерувати ПВП з довільним алфавітом m, заданим періодом повторення та певними, але недостатньо дослідженими властивостями нерозрізнюваності.

Але в указаній роботі залишились нерозглянутими питання управлінння ключами генератора, а по суті розробки криптографічного генератора, а також оцінки рівнів гарантій такого генератора ПВП в частині необоротності, непередбачуваності та нерозрізнюваності [ 2, 4].. Дослідження роботи носять також обмежений характер, так як вони проведені тільки для багатомодульних перетворень над простим полем Галуа

Метою статі є розробка методу генерування ПВП з певним алфавітом символів m, на основі багатомодульних перетворень з використання елементів довільного поля Галуа . Зрозуміло що відносно цього методу необхідно провести комплекс теоретичних та експериментальних досліджень в частині визначення необхідних та достатніх умов забезпечення заданого періоду повторення, основи алфавіту, ймовірності появи символів алфавіту на періоді повторення, якості необоротності, непередбачуваності та нерозрізнюваності с точки зору гарантій[ 2 - 5].

Метод багато модульного перетворення в скінченному полі

Розглянемо метод генерування ПВП з певним алфавітом символів, скажемо m, на основі багатомодульних перетворень, але на основі використання елементів уже довільного скінченного поля Галуа . Для загального випадку будемо вважати, що здійснюється k перетворень елементів розширення поля Галуа , відповідно за модулями та останнім модулем m. Загальними параметрами, яких достатньо для того, щоби генерувати елементи поля , є кортеж , де – незвідний поліном степеню n над полем , а – первісний елемент, вибраний із множини порядку , де – функція Ейлера [ 3 ]. В цьому випадку генерування (формування) елементів поля здійснюється за правилом

. (1 )

Показано [ 6 ], що при виконанні вказаних вище вимог до кортежу , (1) породжує скінченне поле Галуа з періодом повторення . Замітимо, що вказане справедливо для і наступних простих чисел. Причому, при p=2 будемо мати розширення над полем Галуа .

Далі, нехай будуть кортежами загальних параметрів, наприклад поліномів (в тому числі незвідних) , , а – їх степені. В подальшому незвідність поліномів нам потрібна для того, щоби при необхідності забезпечити їх взаємну простоту [ 6 ].

Також нехай степені поліномів (в тому числі незвідних) задовольняють вимогам

, , … , , (2 )

причому основа алфавіту m є довільним числом, а також виконуються нерівності

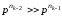, ,…,, . (3 )

Справедливим є твердження 1.

Твердження 1. Детермінований генератор ПВП, що функціонує згідно багато модульного перетворення

(4 )

,

де 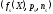кортежі загальних параметрів, m – певне натуральне число, k – ступень багато модульності, (не обов’язково просте), m ціле натуральне, забезпечує генерування ПВП (символів) з періодом повторення , рівно ймовірно і з певною основою алфавіту m, за умови, що:

• виконуються умови (1 ) – (3 ) ;

• модулі (пари поліномів)

(5 )

є взаємо простими, а кортеж є довільним.

В (4) запис – означає, що модуль m подається у вигляді полінома.

При виконанні умов (4)–( 5) забезпечується генерування ПВП (символів) з такими властивостями та характеристиками:

• певною основою алфавіту m;

• періодом повторення ;

• символи генеруються рівноймовірно або "практично" рівно ймовірно;

• ансамблем ізоморфізмів .

Справедливим також є твердження 2.

Твердження 2. Детермінований генератор ПВП, що функціонує згідно алгоритму багатомодульного перетворення

(6 )

,

де K₀+i є плинний ключ генератора, причому K₀ є початковим ключем, а i – ключем сеансу, є не оборотним зі складністю не нижче чим О(n)[ ].

Розглянемо далі частковий випадок твердження 1 та 2 для 3-ьох модульного перетворення. В даному випадку елементи розширення поля Галуа також генеруються згідно (1 ). Але (2 ) – (6 ) приймають вид (7 ) – (10 ).

. (7 )

. (8 )

. (9 )

, (10 )

де як в (4 4.24) K₀+i є плинний ключ генератора, K₀ початковий, а i – ключ сеансу.

Для умов (7) – (10) твердження 1 для трьох модульного перетворення подамо у вигляді теореми 1 .

Теорема 1. Детермінований генератор ПВП, що функціонує згідно трьох модульного перетворення на основі (1 ), за правилами

(11 )

або

(12 )

при виконанні умов (2) – (8), забезпечує генерування ПВП (символів) чисел з певною основою алфавіту m, періодом повторення , рівно ймовірною появою символів на періоді повторення та ансамблем ізоморфізмів .

Доведемо теорему1 4.5 для 3-ьох модульного перетворення. Що стосується останнього модуля m в (11 4.31), то він може приймати довільне значення і будемо його подавати в поліноміальному вигляді. Замітимо, що та в (11 ) незвідні поліноми можуть подаватися над полем , тобто у вигляді полінома степені над .

Відносно періоду повторення.

Оскільки – первісні елементи, то для забезпечення максимального періоду необхідно та достатньо що би був незвідним над полем [ ]. Так як незвідний над полем , то згідно (11) генеруються елементи поля Галуа з періодом 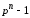, а кожен елемент появляється один раз.

Визначимо ступінь рівно ймовірності появи m –символів (кінцевого алфавіту), тобто визначимо умови, за яких символи m-го алфавіту появляються рівно ймовірно. Будемо задавати символи за допомогою поліномів не вище степені.

Подамо усі елементи поля 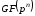у вигляді цілих натуральних чисел від до .

Далі упорядочимо числа в міру збільшення

(13 )

,

де є значення елемента поля .

Приведемо ряд (133 4.33) по модулю , в результаті отримаємо

, (14 )

де .

Послідовність (14) подамо у вигляді

(15 )

,

причому .

Всього в ПВП буде елементів послідовності, дорівнює . При цьому в останньому блоці будуть відсутні елементи послідовності, починаючи з і до та 0.

Далі, символи появляються z раз, – (z-1) раз. Відповідно ймовірності появи елементів будуть

, (16 )

а

. (17 )

Таким чином, на періоді послідовності в результаті виконання перетворення по другому модулю символи появляються з практично однаковою ймовірністю, тобто рівно ймовірно.

Розглянемо етап перетворення по третьому модулю, який згідно теореми 1 може бути довільним числом . При аналізі на частоту перетворення позначимо послідовність як

(18 )

і приведемо її, тобто (4.38), по модулю і отримаємо ряд

, (19 )

Причому .

Аналізуючи ймовірність появи символів отримаємо ті ж оцінки, що і в (16 ) та (17 ).

Також відмітимо, що в (16) нерівноймовірність появи V символів не перевищує 1 в числі появлення символів , а також оцінкою нерівноймовірності для кожного символу .

Таким чином , теорема 1 для 3-ьох модульного перетворення доведена. Також необхідно замітити що наведене доведення теореми 1 може бути розповсюджене і на випадок k модульного перетворення, зрозуміло за умови коли пари поліномів є взаємо простими, а кортеж є довільним, мається на увазі значення модуля m.

У цілому процедура генерування ПВП на основі багатомодульного перетворення може бути зведеною до наступного.

1. Ввести або генерувати загальносистемні параметри – кортежі загальних параметрів згідно вимог твердження 1.

2. Ввести або інсталювати таємний ключ генератора , .

3. Обчислити початкове значення генератора , використовуючи правило

, (20)

де – основний модуль перетворення.

4. Обчислити елемент генератора, використовуючи правило

, (21)

де – номер елемента ПВП, що генерується, – -й елемент послідовності над полем поширення .

5. Обчислити елемент ДГВЧ, використовуючи правило

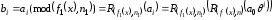, (22)

де .

6. Обчислити елемент ДГВЧ, використовуючи правило

, (23 )

де – номер елемента ПВП, що генерується, – проміжні модулі.

7. Якщо потрібно, то обчислити -е геш-значення від та прийняти його в якості -го випадкового слова, тобто

. (24 )

Схема алгоритму (варіант), що реалізує наведений вище метод генерування ДГВЧ, наведена на рис. 1.

Рисунок 1 – Схема алгоритму генерування детермінованих випадкових послідовностей в скінченному полі порядку - 1 методом багатомодульного перетворення

Висновки

1. На нинішній час розроблено ряд методів та на їх основі засобів формування ПВП, Їх особливістю є те, що вони будуються, як правило, для двійкової основи . Важливою і необхідною є задача розробки методів і засобів генерування ПВП із необхідними властивостями випадковості та довільною (певною) основою алфавіту. В якості перспективного, на наш погляд, класу таких перетворень необхідно назвати клас багатомодульних перетворень.

2. Детермінований генератор ПВП, що функціонує згідно трьох модульного перетворення на основі (11 ) або (12 ) при виконанні умов (2 ) – (8 ), забезпечує генерування ПВП (символів) чисел з певною основою алфавіту m, періодом повторення , рівно ймовірною появою символів на періоді повторення та ансамблем ізоморфізмів .

Додаток А