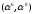Криптографічні перетворення в групі точок еліптичних кривих

6.3.2 Криптографічні перетворення в групі точок еліптичних кривих. Приклади розв’язку задач та задачі для самостійного розв’язання

6.3.2.1 Приклади розв’язку задач

Задача 1.

Скласти точки P1 і P2. P1=(12, 19), P2=(5, 4). Якщо еліптична крива має вигляд , тобто a = 1, b = 1, P = 23.

Розв’язок задачі:

.

Знаходимо в полі G(23) обернений елемент Z, розв’язавши порівняння

7*Zº1 (mod 23).

Це порівняння має розв’язок при Z = 10, тому

l = 15*10 (mod 23) = 12.

= 12² – 12 –5 = 144 - 12 – 5 (mod23) = 127 mod23 = 12 mod23.

=12*(12 - 12) - 19(mod23) = 4mod23.

Таким чином:

P₁ + P₂ = (x₁, y₁) + (x₂, y₂) = P₃ = (x₃, y₃) = (12, 4).

P₃=(12,4).

Задача 2.

Знайти точку, яка дорівнює . . Еліптична крива має вигляд

, тобто a=1, b=1.

Розв’язок задачі:

Спочатку подвоїмо точку , тобто знайдемо .

Знайдемо , використовуючи (1.88)

.

Знайдемо зворотний елемент

; .

Значить .

Використовуючи (1.85)-(1.86) та враховуючи, що х₁=х₂, знайдемо координати х₂ і у₂ точки P₂(x₂,y₂)

;

.

Таким чином: .

Далі знайдемо суму точок P₁+P₂=P₁+2P₁=P₃=(x₃, y₃).

.

Знайдемо , використовуючи (1.87)

.

Знайдемо зворотний елемент

; .

Значить .

Використовуючи (1.85) і (1.86), знайдемо х₃ та у₃

;

.

Таким чином: 3Р₁ =3(5, 4) = (13, 16).

Задача 3.

Нехай є ЕК з рівнянням: , a=1, b=1, p=23.

Перевірити, чи належать такі точки ЕК:

(1, 7), (1, 16).

Розв’язок задачі:

, точка (1,7) не належить ЕК;

, точка (1,16) належить ЕК.

Задача 4.

Знайти порядок базової точки (17, 20). Якщо рівняння еліптичної кривої має вигляд .

Розв’язок задачі:

Для визначення порядку точки (17, 20) на еліптичній кривій знайдемо таке значення d, щоб d*(17, 20) (mod 23) = 0.

Для цього підставимо в останнє порівняння d = 1, 2, 3, … k, та визначимо значення скалярного добутку.

При d = 2 маємо

При d = 3

При d = 4 маємо:

При d = 5

P₁ + Q₃ =Q₄

При d = 6

P₁ + Q₄=Q₅

При d = 7

P₁ + Q₅=Q₆

Таким чином порядок n точки G = (17, 25) на еліптичній кривій дорівнює 7.

Задача 5.

Побудувати , m=4, , .

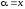Розв’язок задачі:

Поле – може бути задано 16 поліномами не вище третього ступеня, наприклад, поліномами над полем GF (2).

Елементи поля можуть бути задані в двійковому вигляді, тоді, наприклад,

x³+ x²+1Þ1101

x³+1Þ1001.

Операція множення елементів поля виконується в полі GF(P).

Наприклад:

Зведемо цей поліном за модулем f(x) = x⁴+ x+1. У результаті маємо:

Таким чином: (x³+ x²+1)(x³+ 1)(mod (x⁴+ x+1),2) = x³+ x²+x +1Þ1111.

В табл. 1.5 наведені елементи a^j для j=, якщо a = x.

Таблиця 1.5 – Значення a^j

j	0	1	2	3	4	5	6	7
a j	1	x	x2	x3	x+1	x2+x	x3+x2	x3+x2+x+1

Елементи поля можна отримати як a^j = a ^j (mod f(x),2), j=.

Задача 6.

Нехай задано поле , m=4, ,.

Знайти , якщо .

Розв’язок задачі:

Знайдемо :

.

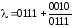Далі знайдемо зворотний елемент для числа 0111, яке подамо поліномом х²+х+1.

Враховуючи, що:

;

.

Знайдемо :

Таким чином:

.

6.3.2.2 Задачі для самостійного розв’язання

1. Нехай є ЕК з рівнянням: , a=1, b=1, p=23.

Перевірити, чи належать точки, що наведені в табл. 1.6, еліптичній кривій:

Таблиця 1.6 – Значення

N	1	2	3	4	5	6	7	8	9	10	11	12
	(3,10)	(3,13)	(4,0)	(5,4)	(5,19)	(6,4)	(6,19)	(7,11)	(7,2)	(9,7)	(9,16)	(17,3)
N	13	14	15	16
	(17,20)	(18,20)	(19,5)	(13,16)

Якщо n= k (mod 17), k – номер в журналі.

Якщо k=17, то k=k+1.

2. Знайти (з попередньої задачі).

3. Знайти , якщо (з попередньої задачі).

4. Знайти і , якщо , а еліптична крива має вигляд ,

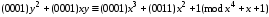	1	2	3	4	5	6	7	8

k – номер за списком, якщо k=8, то .

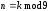6.3.2.3 Контрольні запитання та завдання

1. Дати визначення базової точки ЕК.

2. Запишіть та поясніть формулу складання точок еліптичної кривої над простим полем.

3. Запишіть та поясніть формулу подвоєння точок еліптичної кривої над простим полем.

4. Запишіть та поясніть формулу складання точок еліптичної кривої над розширеним полем.

5. Запишіть та поясніть формулу подвоєння точок еліптичної кривої над розширеним полем.

6. Яким вимогам задовільняє примітивний поліном f(x)?

7. Скільки елементів в полі GF(2^m), якщо m = 4, 9, 81, 160?

8. Скільки елементів в полі GF(P), якщо P = 17, 31, 47, 89, 107, 257?

9. Запишіть елементи поля GF(7).

10. Запишіть елементи поля GF(2³).

11. Запишіть та поясніть рівняння еліптичної кривої над простим полем GF(P).

12. Запишіть та поясніть рівняння еліптичної кривої над розширеним полем GF(2^m).

13. Запишіть та поясніть рівняння еліптичної кривої в проективному вигляді.

14. Що забезпечує використання проективного базису?

15. Порівняйте стійкість RSA криптоперетворення та перетворення в групі точок ЕК.

16. Як можна знайти зворотні елементи в полі GF(q)?