ПРИКЛАДНА КРИПТОЛОГІЯ

ЛЕКЦІЯ №13(3.4)

Тема лекції

« Механізми НШ та їх застосування для забезпечення конфіденційності »

Навчальні питання

13.2 Направлене шифрування з використанням механізмів ISO/IEC 18033 -2

13.2 Направлене шифрування з використанням механізмів ISO/IEC 18033 -2

Додаток А

Механізми направленого шифрування з використанням ISO/IEC 18033 -2

Джерела, що рекомендуються до самостійної роботи

1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія (електронний варіант). Харків, ХНУРЕ, 2011 р.

2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. Харків, ХНУРЕ, 2011 р.

3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.

4. Горбенко Ю.І., Горбенко І.Д. Інфраструктури відкритих ключів . Системи ЕЦП. Теорія та практика. Харків. Форт. 2010 , 593с.

Додаткова література

1.В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.

2. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с

10. Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с

13.1 Направлене шифрування в кільцях зрізаних поліномів (приведення в решітках)

13.1.1 Сутність та стан розробки алгоритму ntru

Всередині 1990-х років групою математиків (Джефрі Ховстейн, Джилл Піфер та Джозеф Сильверман) було розроблено новий метод і на його основі алгоритм направленого шифрування, який отримав назву NTRU. Його офіційно було представлено на конференції CRYPTO 96. Розробниками алгоритму всім бажаючим було надано доступ до повного опису криптосистеми NTRU та результатів попередньому аналізу його криптографічної стійкості. В подальшому метод та алгоритм НШ з урахуванням пропозицій спеціалістів було дороблене, наприклад збільшено розміри параметрів алгоритму з метою підвищення криптографічної стійкості. Надалі Коперсміт та Шамір в своїх роботах, що були пов’язані з крипто аналізом системи NTRU, довели, що найбільш ефективним методом крипто аналізу цієї системи є атака за допомогою приведення в алгебраїчній решітці.

Надалі вчені Jaulmes та Жу в 2000 році звернули увагу на те, що загальні параметри для NTRU потрібно вибирати з урахуванням атак на адаптивно підібраних повідомленнях, а також на те, що значення параметрів повинні обиратися з урахуванням і інших вимог . Також Howgrave - Грэм, Проос та інші показали, що параметри також повинні обиратися, для того щоб не перевищувати рівень некоректно розшифрованих повідомлень.

Основною перевагою цього алгоритму НШ є те, що він працює набагато швидше уже використовуємих алгоритмів з відкритим ключем, наприклад RSA. Тобто, основною перевагою NTRU перед іншими алгоритмами НШ, є зменшена складність, і як наслідок, підвищена швидкодія. Так для за шифрування та розшифрування повідомлення довжиною з N символів необхідно O(N²) операцій для алгоритмуNTRU, в той час як для RSA потрібно O(N³) операцій. Алгоритм NTRU є запатентованим NTRU Cryptosystem.

У алгоритмі НШ NTRU усі операції здійснюються в кільці зрізаних поліномів ( див. 1.9). Криптографічна стійкість алгоритму заснована на складності вирішення задачі знаходження короткого вектора у заданій решітці . Показано, що крипто стійкістьNTRU-167 (параметр N = 167) приблизно відповідає RSA-512, стійкість NTRU-263 та NTRU-503 приблизно відповідає RSA-1024 та RSA-2048 відповідно.

В квітні 2011 року Американським комітетом (Accredited Standards Committee) X9 NTRU (NTRUEncrypt) був затверджений у вигляді стандарту ANSI X9.98. Вказується, що NTRUEncrypt є найшвидшим алгоритму асиметричного шифрування, він забезпечує в певних умовах швидкодію на чотири порядки вище ніж RSA ( за рахунок розпаралелювання).

Розробниками NTRU запропоновано також «полегшену» версію криптографічного алгоритму, яку можна використовувати для шифрування даних смарт – карт тощо. При цьому компанія стверджує, що по надійності і принципом дії алгоритм схожий з RSA, проте набагато простіше і не вимагає великих обчислювальних потужностей. Таким чином , алгоритм NTRU, що поданий в стандарті США Х9 .98, є досить перспективним, але вимагає , на наш погляд, подальших досліджень.

На рис. 13.5 класифікація відомих версій криптосистем, яка ґрунтується на доведенні криптографічної стійкості на використанні методів алгебри приведення в решітках.

Рис. 13.5 - Класифікація криптосистем на основі завдання приведення в решітках

2. Параметри алгоритму NTRU

Основні математичні поняття, що потрібні для розуміння алгоритму NTRU наведені в розділі 1.9.

Загальними параметрами алгоритму NTRU є :

N – степінь зрізаного кільця поліномів, при чому елементи кільця представляються у вигляді поліномів степеня N – 1;

більший модуль - ціле число q, що використовується при обчисленні кільця поліномів. Модуль q не повинен мати спільних дільників з меншим за модуль q модулем p. В стандарті Х.9913.1 в якості q використовується ступінь числа 2( 2¹¹= 2048), а p=3.

Параметр N використовується для визначення набору кільця поліномів, у якому виконуються криптографічні перетворення. Це множина R усіх поліномів, ступінь яких менше ніж N, що позначається як

R=Z[X]/(X^N-1) (13.47).

Кільце R (13.47) ще не є зрізаним, зрізання виникає при приведенні коефіцієнтів поліномів за модулем q. Тому результат обчислення для Z/q Z дає зрізане кільце поліномів , яке будемо позначати як

R_q = (Z/ q Z)[X]/(X^N- 1) (13.48) .

У таблиці 13.7 наведені параметри основного алгоритму разом з поясненням кожного з них[ ]. У таблиці 13.8 [ ] наведені значення параметрів для різних рівнів безпеки, які рекомендує NTRU Cryptosystem. Взагалі алгоритм NTRU фактично носить імовірнісний характер, тобто існує невелика ймовірність помилки при розшифрування. Але при відповідному виборі параметрів, ймовірність помилки розшифрування може дорівнювати

10^-25 або менше. Значення параметрів , що наведені в таблиці 13.8 мають малу імовірність помилки розшифрування. Ці параметри рекомендовані NTRU Cryptosystem

для використання в комерційних додатках.

Таблиця 13.7 - Ключі та параметри алгоритму NTRU

Параметр	Коротке пояснення параметру
N	Розмір зрізаного кільця многочленів R. Елементи кільця представлені у вигляді поліномів степеня N – 1(відкритий)
q	Великий модуль, згідно якому приводиться по модулю кожний коефіцієнт многочлена у кільці R (відкритий)
p	Малий модуль, по якому приводиться кожний многочлен (відкритий)
f	Поліном, що є особистим (таємним) ключем
g	Поліном , який використовується для генерації відкритого ключа h з особистого f (таємний, але знищується після першого використання)
h	Відкритий ключ, також поліном
r	Випадковий поліном «забілювання» (таємний, але знищується після першого використання)
df	Поліном f повинен мати df коефіцієнтів 1 та df-1 коефіцієнтів - 1
dg	Поліном g повинен мати dg коефіцієнтів 1 та dg коефіцієнтів - 1
dr	Поліном r повинен мати dr коефіцієнтів 1 та dr коефіцієнтів - 1

Таблиця 13.8 - Значення розмірів параметрів для різних рівнів безпеки NTRU

Рівень безпеки	N	q	р
Помірний	167	128	3
Стандартний	251	128	3
Високий	347	128	3
Надвисокий	503	256	3

2. Алгоритм шифрування NTRUEncrypt

Корпорацією NTRU Cryptosystem опубліковано декілька версій алгоритму NTRU, два з них були реалізовані в цьому проекті. Повний та детальний опис основних алгоритмів, а також ілюстративний приклад наведені в [17.7 ]. Розглянемо сутність алгоритму.

Генерування асиметричної пари ключів. Нехай генерування асиметричної пари розпочинає абонент В. Для цього він вибирає(генерує) згідно вимог таблиці 13.7 два випадкових поліномів f і g, що визначені в кільці R. Причому поліноми f і g повинні мати мультиплікативно зворотні поліноми в кільці по модулю загальних параметрів р і q. Позначимо такі мультиплікативно зворотні значення для поліному f (F _p )та відповідно. Вони повинні бути розраховані тільки точно для обраного f.

Необхідно відмітити, що в стандарті Х9.98 особистий ключ f повинен обчислюватись згідно рекомендації [ ] в кільці поліномів (Z/ q Z)[X]/(X^N- 1):

f = (1 +p F) mod q, (13.49)

де р = 3 – загальний (доменний параметр), а F випадковий поліном, алгоритм генерування якого визначено в стандарті.

Далі абонент В обчислює свій відкритий ключ у вигляді многочлену h у кільці поліномів (Z/ q Z)[X]/(X^N- 1) згідно правилу

h = *g) mod q , (13.50)

де g, як уже вказувалось, є також випадково обраний згідно вимог таблиці 13.7 поліном у кільці R_q. Поліноми f і g крім того що повинні бути "випадково" обраними в R_q, але також повинні мати конкретну кількість коефіцієнтів, 0, +1 і -1 згідно таблиці 13.7, тобто обрані випадково із множини поліномів з фіксованим числом символів коефіцієнтів 0, +1 і -1. Особистий (таємний) ключ у вигляді многочлену f разом із зворотними F_p) та (F_q) є таємними ключовими даними, h – відкритим ключем. Значення N, p і q є параметрами алгоритму шифрування NTRU. В цілому, таким чином, асиметричною парою ключів є (f, h) пара особистого та відкритого ключів, що являються поліномами степені N-1.

Алгоритм зашифрування. Нехай абонент А хоче направлено зашифрувати для абонента В двійкове повідомлення m. Для цього А повинен знати справжні загальні параметри N, p і q та відкритий ключ абонента В - h_b. Далі абонент А генерує «випадково» згідно таблиці 13.7 у кільці R_q многочлен r_а ( по суті ключ сеансу). Безпосередньо абонент А зашифрування виконує шляхом обчислення значення

c=( r_а*h_b + m) mod q (13.51)

В (13.51) множення r_а на h_b виконується у рамках розміру кільця, як зазначено вище, тобто у вигляді згортки за модулем q, а повідомлення m додається за модулем q.

Алгоритм розшифрування. Для розшифрування криптограми с абонент В повинен мати справжні загальні параметри N, p і q . Розшифрування здійснюється засобом згортки поліномів N-1 степені в кільці (Z/ q Z)[X]/(X^N- 1): особистого ключа f_b та криптограми с як

a= f_b*с mod q. (13.52)

Надалі коефіцієнти полінома а для отримання повідомлення m приводяться по модулю в інтервалі [ А, А+q-1 ], а також по модулю p для отримання кандидата в розшифроване повідомлення m^’.

Необхідно відмітити, що при розшифруванні випадково можемо отримати повідомлення, яке буде відрізнятися від вихідного. Це може відбутися за рахунок виконанні операції спочатку за модулем q, а потім за модулем p. На практиці, якщо правильно обрати загальні параметри, що наведені в таблиці 13.7, імовірність появи такої помилки не перевищує 2^-100 (10 ^-30)[ ].

Сутність направленого розшифрування полягає в тому, що абонент, який намагається розшифрувати багаточлени – криптограми, має знати цілісні й справжні загальні параметри та особисту пару ключів (f(x), f_p(x)). За таких умов розшифрування може здійснюватись у такій послідовності.

1. Обчислюється згортка особистого ключа та криптограми у вигляді

f(x)* С(x) (mod q) (9.120)

У результаті отримуємо:

f(x)* С(x) (mod q) = (f(x)* p* r(x)*h(x) + f(x)* М(х)) mod q) = (f(x)* p* r(x)* f_q(x)* g(x) + f(x)* М(х)) mod q) = а(х).

З урахуванням (9.117), тобто що f(x) * f_q(x)=1(mod q), маємо:

а(х) = (p* r(x)* g(x) + f(x)* М(х)) mod q). (9.121)

2. Обчислюється значення (9.121) за модулем меншого параметра р, у результаті маємо:

а(х)(mod р) = (p* r(x)* g(x) + f(x)* М(х)))(mod р) (9.122)

У (9.122) p* r(x)* g(x)(mod р) =0, тому

b(x) = f_p(x)* а(х)(mod р) = f_p(x)* f(x)* М(х)(mod р) = М(х), (9.123)

оскільки f(x) * f_p(x)=1(mod p).

Таким чином, доведено, що направлене шифрування в кільці зрізаних багаточленів R є оборотним.

2. Попередні оцінки алгоритму направленого шифрування NTRU

Основними атаками, що можуть бути реалізовані на алгоритм NTRU, на наш погляд, є такі:

• атака з адаптивно підібраним текстом;

• атаки,що пов’язані з некоректним вибором загальних параметрів :

• атаки, що пов’язані з помилками при генеруванні ключів та параметрів;

• атаки, що пов’язані з використанням при крипто аналізі алгоритмі, що реалізуються на квантових комп’ютерах.

Для вирішення задачі пошуку найближчого вектору (найкоротшого) в теорії зведення решіток використовується метод LLL (Lenstra, Lenstra and Lovasz)[ ]. Цей алгоритм знаходить достатньо невеликий вектор за поліноміальний час, але у загальному випадку алгоритм не дозволяє знайти найкоротший вектор. Існує багато вдосконалень цього методу, що зроблені вченими Schnorr, Euchner[ ]. Ці вдосконалення відомі як «глибока вставка», «блочне зведення», «зрізання». Але складність цих методів для вирішення задачі пошуку найменшого вектора в загальних решітках є експоненційною.

Також складною задачею відносно криптосистеми NTRUEncrypt Public Key є пошук найкоротшого вектора в решітці великого розміру. Сьогодні найкращим з методів крипто аналізу цієї крипто системи вважається метод зведення в решітках LLL. Для того щоб перевірити перевірки на практиці захищеність системи NTRUEncrypt, за допомогою метода LLL було вирішено багато задач знаходження найкоротшого вектора для решіток різних розмірностей. За результатами цих експериментів було отримано графічне представлення часу, необхідного для знаходження необхідного вектору для заданої решітки. З цього графіку було екстрапольовано час здійснення крипто аналізу для решіток більшої розмірності, які використовуються на практиці, та за отриманими результатами було отримано відповідні параметри для NTRUEncrypt. Вказані результати наведені в 9розділі детально.

В таблиці 13.9 для порівняння, наведені оцінки оцінку часу крипто аналізу відносно NTRUEncrypt, RSA та EC-DSA криптосистем для різних рівнів безпеки[ ]. В якості основного критерію рівня безпеки використовується довжина ключа блокового симетричного шифру.

Таблиця 13.9

Рівень безпеки ( довжина симетричного шифру, біт)	Оцінка часу крипто аналізу, MIPS-years	Криптосистема
		RSA	NTRU X9.98-2010			EC-DSA
80(2TDEA)	109	1024	N=263		n =160 – 223
112(3TDEA)	1017	2048	N=401		n = 224 – 255
128(AES-128)	1023	3072	N=613		n = 256 – 383
192(AES-192)	1041	7680	N=500		n = 384 – 511
256(AES-256)	1063	15360	N=1171		n = 512 +

В таблиці 13.10 наведено оцінки рівня безпеки алгоритму NTRU для стандарту X9.98-2010[].

Таблиця 13.10 - Оцінки рівня безпеки X9.98-2010

Рекомендований рівень безпеки, біт	N	q	d f	Оцінка рівня безпеки
112	401	2048	113	154.88
112	541	2048	49	141.766
112	659	2048	38	137.861
128	449	2048	134	179.899
128	613	2048	55	62.385
128	761	2048	42	157.191
192	677	2048	153	276.736
192	887	2048	81	245.126
192	1087	2048	63	236.586
256	1087	2048	120	376.32
256	1171	2048	106	327.881
256	1499	2048	79	312.949

В таблиці 13.11 наведені результати порівняння розмірів ключів для NTRU,RSA та еліптичних кривих(EC)[ ]. Причому прийнято, що для NTRU та RSA розмір блоку шифротексту порівняний з розміром відкритого ключа.

Таблиця 13.11 — Порівняння розмірів ключів для NTRU та інших алгоритмів з відкритими ключами

Рівень стійкостіk, біт	NTRU		RSA		ЕC
	LPub	LPri		LPub, LPri		LPub, LPri
112	4411	802		2048		224
	5951	980
	7249	760
128	4939	898		3072		256
	6743	1100
	8371	840
192	7183	1306		7680		384
	9757	1620
	11957	1386
256	9383	1706		15360		512
	12881	2332
	16489	1738

В таблиці 13.11 використані такі позначення:

• LPub – довжина відкритого ключа в бітах

• LPri — довжина особистого ключа в бітах

Наскільки це можливо, детальніше результати оцінки криптографічної стійкості алгоритму Х9.98, представлені в 9 розділі.

Необхідно відмітити, що метод, який лежить в основі NTRU, відомий та досліджується порядку 20 років, тобто пройшов випробовування часом. Він суттєво дороблявся та удосконалювався. Як наслідок, після 15 річних доробок він прийнятий в якості стандарту ANSI Х9.913. на наш погляд, в тексті опису стандарту є ще неточності та неоднозначності, але враховуючи можливості суттєвого підвищення швидкодії, його можна вважати перспективним.

Особливої уваги заслуговують атаки за допомогою квантових комп’ютерів. Так, для алгоритму LBP-PKE [33], запропоновано метод вирішення задач зведення в решітках для квантового комп’ютера, При цьому складність цього методи має експоненційних характер, але потенційно в роботах [34, 35, 36, 37, 38] показано можливість прискорення до рівня суб експоненційної складності.

Важливим є те, що компанія NTRU Cryptosystem стверджує, що з використанням алгоритму, представлений в стандарті Х9.98 можна реалізувати ефективний захист від несанкціонованого доступу засобом застосування простих пристроїв. Для цього розроблено спрощену версію криптографічного алгоритму NTRU, яку можна використовувати для шифрування з застосуванням смарт - карт і ярликів у пунктах продажу. Також стверджується , що по надійності і за принципом дії алгоритм схожий з RSA, проте набагато простіше і не вимагає великих обчислювальних потужностей. Також компанія стверджує, що

Швидкодія роботи такої системи на смарт – картці порівнянна зі швидкістю обробки криптографічного алгоритму RSA на Pentium.

За даними компанії[ ], безконтактні смарт - карти з RSA коштують близько $ 3 - $ 5, а GenuID, за твердженням NTRU, будуть коштувати близько $ 0,5 - $ 1. В даний час до розробок NTRU проявили інтерес такі компанії,як Texas Instruments і Sony, вклавши розробку $ 38 млн.

В таблиці 13.12 наведені результати оцінки швидкостей NTRU , RSA, DSA та EC на процесорі з частотою 2 ГГц.

Таблиця 13.12 — Порівняння швидкостей NTRU, RSA и ЭК

Уровень стойкости(біт БСШ)	Операций/секунда
	NTRU	ЭК	RSA
112	10638	951	156
128	9901	650	12
192	6849	285	8
256	5000	116	1

На останок відмітимо, що все таки основною перевагою NTRU є суттєво підвищена в порівнянні з RSA, DSA та EC швидкодія. За даними компанії Security Innovation[ ] , що займається розробкою NTRU, алгоритм NTRU в режимі направленого шифрування забезпечує збільшення швидкодії до 200 разів.

13.2 направлене шифрування з використанням механізмів ISO/IEC 18033 -2

Зважаючи на суттєву важливість застосування алгоритмів НШ на практиці, на міжнародному рівні при виконанні Європейського проекту «Nessie» 2000 - 2004р., особлива увага була звернута на реалізацію висунутих вимог для алгоритмів та протоколів НШ [ ]. В подальшому на основі отриманих результатів, пропозицій та рекомендацій в 2006р. був прийнятий міжнародний стандарт ISO/IEC 18033 -2 « Інформаційна технологія — Методи захисту — Алгоритми захисту — Частина 2: Асиметричні шифри».

13.2.1 Вимоги до НШ ISO/IEC 18033 -2

До криптографічних алгоритмів (в термінах проекту «Nessie» крипто примітивів) були висунуті за основними критеріями такі вимоги[ ].

1) Захищеність крипто примітивів від крипто аналітичних атак. Сутність критерію в тому, що складність усіх відомих крипто аналітичних атак повинна бути не менше складності атаки типу „ брутальна сила ”.

2) Особливість конструкції та відкритість структури. Сутність цього критерію в тому, що представлені крипто примітиви повинні мати зрозумілу та легко аналізуємо структуру, а також базуватись на надійних математичних та криптографічних принципах.

3) Стійкість до модифікацій. Сутність цього критерію в тому, що крипто примітиви, які досліджуються, повинні бути стійкими в певній мірі до таких модифікацій як зменшене число циклів криптографічного перетворення, скорочення компонентів крипто примітивів тощо.

4) Статистична безпечність крипто алгоритму. Сутність цього критерію в тому, що відносно аналізує мого крипто примітиву повинні бути відсутні статистичні атаки на криптоалгоритм в цілому, на криптографічне перетворення та на схеми виробки ключів. При цьому складність статистичних атак повинна бути не менше складності атаки типу „ брутальна сила ”.

5) Обчислювальна складність (швидкість) виконання криптографічних операцій. Згідно цього критерію складність (швидкість) виконання прямого та зворотного крипто перетворень, а також складність (швидкість) роботи з ключем, повинна бути не більше допустимої величини.

6) Складність програмної, апаратної та програмно-апаратної реалізацій. При програмній реалізації вона повинна оцінюватись розміром вихідного коду, необхідним об’ємом пам’яті, швидкодією на різних платформах (операційних системах). При апаратній реалізації оцінюється кількістю вентилів, необхідних для реалізації та швидкістю виконання криптографічних перетворень.

Згідно з матеріалами роботи [6] зробимо формальне визначення алгоритму асиметричного шифрування. В матеріалах NESSIE вважається, що захист алгоритмів шифрування повинен бути імовірнісним. Також, зважаючи на певну специфіку для розуміння алгоритмів НШ слідуючи [ ] введемо ряд визначень

Визначення13. 1. Асиметрична система шифрування . Це трійка детермінованих алгоритмів

(G,E, D).

Перший алгоритм G називають алгоритмом генерації ключів і він повинен виконуватися один раз - при установці системи. Вихідні дані алгоритму - параметр I_l безпеки й випадкова послідовність r певної довжини, а також пара ключів (p_k,s_k). Ключ p_k називають відкритим ключем, і він повинен бути доступний усім, хто бажає зашифрувати повідомлення. Ключ s_k називають особистим (таємним ) ключем.

Другий алгоритм E є алгоритмом зашифрування. На його вхід подається повідомлення m, відкритий ключ pk і випадкове число r певної довжини, а на вихід подається зашифрований текст(криптограма) C.

Третій алгоритм D є алгоритмом розшифрування. На його вхід подається шифротекст і особистий ключ (який може включати елементи відкритого ключа), а на вихід подається повідомлення m¢ або символ помилки ^.

Визначення 13.2. A- ймовірнісна машина Тюрінга, що за час не більше ніж t, приводить до рішення проблеми з імовірністю не менше .A- атакуючий(крипто аналітик) для схеми асиметричного шифрування - ймовірнісна машина Тюрінга, що за час не більше ніж t, робить якнайбільше запитів до оракула виконання розшифрування (decryption oracle) і успішно зламує схему з імовірністю не менш ніж.

Звичайно, імовірність успіху залежить від одиниць виміру часу t- якщо час вимірюється в роках, то слід очікувати більш високу ймовірність успіху в 1 одиницю часу, чим якби час вимірювався в секундах. Надалі приймається, що одна одиниця часу дорівнює часу, потрібному для однієї операції розшифрування.

Однак все ще є проблема із цим підходом. Щоб довести, що система є настільки ж безпечною, як вимагалося в умовах вимог проекту NESSIE, потрібно довести відсутність «сильного» (третього рівня) крипто аналітика. Щоб зробити це, потрібно представити доказ, що існує крипто аналітик, маючи на увазі відсутністьоракула для деяких криптографічних проблем, які заслуговують на довіру.

Модель крипто аналітика та методи крипто аналізу, що можуть бути застосованими при оцінці стійкості асиметричних НШ, представлені в 9 розділі монографії.

Рекомендації щодо застосування НШ. Аналіз викладених в ISO/IEC 18033-2 матеріалів, дозволив зробити висновок, що матеріали стандарту в основному відповідають вимогам коректності їх подання.

Алгоритми асиметричного шифрування, що розглянуті в Міжнародному стандарті ISO/IEC 18033-2 перше видання 2006-05-01, можуть знайти використання й при вирішенні задач захисту інформаційних ресурсів в національних інформаційних системах (ІТС), особливо якщо орієнтуватись на інтеграцію національних технологій захисту інформації з іноземними.

13.2.2 Механізм НШ ACE-KEM

Криптосистема( механізм) ACE-KEM заснована на роботі Cramer і Shoup [41]. Вона була представлена на конкурс NESSIE IBM. Повний перелік вимог до криптосистеми ACE-KEM наведений в [42]. Її можна також розглядати як криптографічний механізм або протокол.

Розглянемо вимоги та особливості криптосистеми ACE-KEM. Вимагається, щоб один абонент або процес міг генерувати кортеж параметрів і відкритих ключів С та конфіденційний ключ К , використовуючи відкриті ключі і параметри іншого, а також особисті (таємні ) свої ключі сеансу. Інший абонент чи процес, що генерував асиметричні пари ключів і володіє їхніми особистими(таємними) складовими, міг відновити конфіденційний ключ, використовуючи відкритий кортеж другого та свої таємні ключі.

Тобто,нехай абонент A генерує кортеж відкритих параметрів та ключів p _k та особистий кортеж ключів s_k. В подальшому тільки А володіє особистими ключами ключі s_k, а відкриті

p _k він передає відповідним чином абоненту В. При необхідності абонент В може обчислити конфіденційний ключ К, використовуючи тільки відкриті параметри і ключі абонента А - p _k(інкапсуляція ключа). Після цього абонент передає абоненту А кортеж С. Наприкінці абонент А , використовуючи кортеж С абонента В та свої, генеровані на першому етапі особисті ключі , методом де капсуляції також обчислює таємний ключ К.

таким чином механізм (протокол) складається з виконання наступних алгоритмів:

• генерування ключів(скажемо виконує абонент А);

• інкапсуляції ключів (скажемо виконує абонент В);

• де інкапсуляції ключів (виконує уже тільки абонент А).

Генерація ключів. ACE-KEM крипто система розроблена для випадку абстрактної групи і може бути реалізована як на еліптичній кривій так і в мультиплікативній групі цілих чисел для деякого модуля. Група є адитивною, елементи групи позначаються заголовними буквами (як у групі точок еліптичної кривої). Припускається, що група є циклічною, з деяким генератором (первісним елементом) P порядку p, і що p має довжину, що дорівнює прийнятому параметру безпеки l.

Алгоритм генерації ключів є імовірнісним алгоритмом, вхідними даними для нього є параметри групи (Р, р. Алгоритм генерації виконується у такій послідовності.

1). Користувачем, що є отримувачем, генеруються випадкові й незалежні цілі таємні числа

(13.54)

2). Користувачем, що є отримувачем, обчислюються відкриті ключі(параметри)

, ,та (13.55)

3). Користувачем, що є отримувачем, визначається (встановлюється) відкритий кортеж параметрів та ключів

p_k=(P, p, X, Y, Z, l) (13.56)

й загальний кортеж параметрів та ключів, що містить особисті(таємні) ключі та кортеж відкритих параметрів і ключів p_k, тобто

s_k=(w, x, y, z, p _k). (13.57)

4). Для використання виводиться пара кортежів ключів та параметрів (p_k, s_k).

Алгоритм інкапсуляції ключів. Алгоритм інкапсуляції є імовірнісним алгоритмом, для якого вхідними даними є відкритий ключ p_k. В алгоритмі використовується загальновідома та погоджена функція гешування Hash( *) й функцію вироблення ключів KDF(*). Алгоритм інкапсуляції виконується у такій послідовності.

1). Користувачем, що є відправником, за допомогою RNG генерується випадкове ціле число

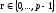. (13.58)

2). Користувачем, що є відправником, обчислюється

. (13.59)

3). Користувачем, що є відправником, обчислюється

. (13.60)

4). Користувачем, що є відправником, обчислюється

. (13.61)

5). Користувачем, що є відправником, обчислюється

(5.62)

6). Користувачем, що є отримувачем, обчислюється

(13.63)

7). Користувачем, що є отримувачем, формується кортеж відкритих параметрів та ключів

(13.64)

8). Користувачем, що є відправником, обчислюється ключ

(13.65)

9). Виводиться інкапсульована пара ключів та параметрів (K, C).

Необхідно відмітити що ключ К є направленим на отримувача, у тому змісті що зашифрувати може кожен хто володіє парою (K, C), по суті хто володіє (13.56).

Алгоритм інкапсуляції ACE-KEM представлений на рис. 13.6.

Розшифрувати, або у загальному випадку зробити зворотне перетворення, може тільки той користувач, що володіє кортежами ключів та параметрів (13.57) та (13.64).

Рис.13.6 – Алгоритм інкапсуляції ACE-KEM.

Алгоритм де капсуляції ключів. Алгоритм декапсуляії є детермінованим алгоритмом, вхідними даними для якого є інкапсульований ключ (13.64) C і особистий (таємний) ключ (13.57) s_k. В алгоритмі також використовується попередньо погоджена функцію гешування Hash( *) й функцію вироблення ключів KDF(*). Задачею де інкапсуляції є обчислення користувачем, що генерував особистий ключ (13.57) s_k, обчислити секретний ключ К, зрозуміло використовуючи С та s_k.

Алгоритм виконується за таким способом.

1). Отримується доступ до кортежу інкапсульованих ключів C = (C1, C2, C3).

2). Обчислюється геш - значення від С₁ та С₂, тобто

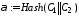. (13.66)

3). Обчислюється значення параметру

. (13.67)

4). Перевіряється що

(13.68)

Якщо не виконується, то зашифрований текст невірний (Invalid Ciphertext) і закінчити виконання алгоритму.

5). Перевіряється що

(13.69)

Якщо не виконується, то зашифрований текст невірний (Invalid Ciphertext) і закінчити виконання алгоритму.

6). Обчислити значення

. (13.70)

7. Обчислити значення таємного ключа

. (13.71)

13. Вивести значення таємного ключа для його використання K.

Висновки та рекомендації відносно механізм ACE-KEM . За результатами аналізу механізму ACE-KEM можна зробити такі висновки.

1). Генерує асиметричну пару кортежів параметрів (p_k, s_k) один абонент, скажемо А, причому відкритий кортеж p_k він передає абоненту В. Але особистий кортеж

s_k він залишає тільки у себе, тобто тільки він володіє ними.

2). Абонент В, отримавши p_k , може генерувати розділюваний з абонентом А ключ К, а також кортеж С, використовуючи відкриті параметри та ключі абонента А, тобто інкапсолювати ключ.

3). Наприкінці абонент А може також обчислити ключ К засобом його де інкапсулювання, але за згоди абонента В, отримавши від нього відкритий кортеж С.

4) . Таким чином, механізм ACE-KEM реалізує направлене шифрування , так як інкапсуляція виконується на відкритому ключі (кортежі) іншого абонента, а де інкапсуляція на особистому ключі(кортежі) абонента.

5). При де інкапсуляції перевіряється цілісність та справжність відкритого ключа та перевіряється справжність іншого абонента(перевіряється автентичність іншого абонента).

6). Можна говорити про неспростовність абонента, що генерує особисті ключі. Наприклад в нашому випадку А. неспростовність абонента В може бути реалізовано засобом передачі відкритого кортежу С через третю довірену сторону.

Аналіз безпеки механізму ACE-KEM. Більш докладний аналіз безпеки ACE-KEM наведений в [48, 44].

Основна перевага ACE-KEM полягає в тому, що безпека схеми може бути доведена без використання евристичної випадкової моделі оракула. Це поєднується одночасно з доказом безпеки для універсальної гібридної конструкції, щоб формувати механізм , що є доказово безпечним без потреби у випадкових оракулах.

Доведення безпеки для ACE-KEM [41] приводить проблему злому ACE-KEM змісті до проблеми вирішення розв’язуваній Діффі - Геллмана проблеми (decisional Diffie-Hellman problem) в групі, що генерована P.

Поряд з більшістю інших асиметричних механізмів шифрування, ACE-KEM вразлива до атаки дефектів (fault attack). Механізм також уразливий силовому аналізу в процесі скалярного множення з дефектами на еліптичній кривій.

13.2.3 Механізм НШ ECIES

Криптосистема ( механізм) ECIES реалізує направлене шифрування і розроблена при виконанні проекту NESSIE Certicom Corp[ ]. Спочатку розглянемо сутність механизму, а потім проведемо його аналіз [50]. Детально питання крипто перетворень в групі точок еліптичних кривих розглядаються в підрозділі 13.6.

При реалізації механізму необхідно ( див підрозділ 2):

• отримати справжні загальні параметри для еліптичної кривої(підрозділ 13.6);

• кожен абонент генерує асиметричну пару ключів ( (див. підрозділ 13.6) );

• реалізується зашифрування повідомлення та виробляється код автентифікації для криптограми;

• здійснюється контроль цілісності прийнятої криптограми .

Генерація асиметричної пари ключів. Припустимо, що значення n порядку базової точки Р еліптичної кривої дорівнює параметру безпеки l . Алгоритм генерації ключів для механізму ECIES є імовірнісним алгоритмом, для якого вхідними даними є загальні параметри (а, b, n= p, P=G, l =n)(підрозділ 13.6).

Генерація ключів. Генерація ключів виконується в такій послідовності.

1). Випадковим образом генерується ціле особисте( таємне) число s із інтервалу ( 1, 2, …, n-1) , тобто

. 1n-1 (13.72)

2). Обчислюється відкритий ключ у вигляді точки еліптичної кривої

W = s G (13.73)

3). Формується відкритий кортеж p_k та конфіденційний s_k

й . (13.74)

4). Виводиться асиметрична пара ключів та параметрів

(13.75).

Алгоритм зашифрування. Алгоритм шифрування - імовірнісний алгоритм, для якого вхідними даними є повідомлення й відкритий ключ. Можуть також використовуватись узгоджені функції, які є доступними всім абонентам. Вони включають функцію вироблення ключів, алгоритм автентифікації повідомленьі симетричну схему шифрування.

Алгоритм виконується у такій послідовності.

1). Генерується випадкове ціле число

. (13.75)

2). Обчислюється відкритий ключ сеансу у вигляді точки еліптичної кривої

(13.77)

3). Обчислюється точка еліптичної кривої

. (13.78)

4). Перевіряється, що

Q O (13.79)

Якщо це так, то виводиться Invalid Encryption і виконання алгоритму зупиняється.

5). Вибирається x-координати точки .

6). Обчислюється ключ

(13.80).

7). Надалі K використовується як E _K і М _К, де E_K - ключ для симетричної схеми шифрування і М _К - підходящий розмір ключа для схеми автентифікації повідомлення.

8). Повідомлення m зашифровується, використовуючи симетричну схему шифрування на ключі E_K, тобто

. (13.81)

9). Для шифротексту обчислюється код автентифікації повідомленняна ключі автентифікації M_K, тобто

(13.82).

11. Формується кортеж криптограм криптограма

. (13.83)

Алгоритм розшифрування. Алгоритм розшифрування - детермінований алгоритм, вхідними даними якого є криптограма C і особистий ( таємний) ключ s_k. В алгоритмі також використовуються попередньо узгоджені функцію вироблення ключів , алгоритм автентифікації повідомленняй симетричний алгоритм шифрування (Sym.Encrypt, Sym.Decrypt).

Алгоритм розшифрування виконується за таким способом.

1). Криптограма С подається у вигляді

. (13.84)

2). З використанням особистого ключа обчислюється

. (13.85)

3). Перевіряється що . Якщо так, вивести Invalid Ciphertext і зупинити виконання алгоритму.

4). Вибирається x-координати точки .

5). Обчислюється ключ

(13.86).

.6). Надалі K використовується як E _K і М _К, де E_K - ключ для симетричної схеми шифрування і М _К - підходящий розмір ключа для схеми автентифікації повідомлення

7). Перевірити що - вірний код автентифікації повідомлення для на ключі M_K, тобто що

(13.87).

У противному випадку вивести Invalid Ciphertext і зупинити виконання алгоритму.

8). Розшифрувати криптограму , використовуючи симетричну схему шифрування на ключі E_K, тобто отримати

(13.88).

9. Вивести відкритий текст повідомлення m.

Аналіз безпеки механізму ECIES. Докладно результати аналізу безпечності механізму наведені в [51], а також деякі аспекти наведені в розділі 9.

Оцінка рівня безпеки для механізму ECIES наведений в [52]. В ньому дається оцінка безпеки механізму DHAES, що є подібним до ECIES, але визначений на абстрактній циклічній групі порядку p. При цьому DHAES відрізняється від ECIES способом генерації симетричного ключа K який, в DHAES одержують із Q і С₁. Доказ безпеки показує, що, якщо передбачена симетрична схема шифрування й MAC є безпечними в деякому змісті, то проблема злому схеми приводиться до проблеми розрізнення вихідних дані функції вироблення ключів від випадкового рядка того ж самого розміру. Доказ захисту для ECIES в універсальній моделі групи запропонований в [53].

ECIES власне кажучи приклад ECIES-KEM (див. 13.13.3), яка використовується зі специфічним механізмом інкапсуляції [42]. Нижче наводиться механізм ECIES-KEM,який, на наш погляд є більш гнучким, чим ECIES.

13.2.4 Механізм НШ ECIES-KEM

Механізм ECIES-KEM ніколи не був формально представлений в проекті NESSIE. Він розглядався NESSIE, оскільки де факто це стандарт для криптосистеми KEM-DEM і тому що механізм ECIES-KEM був стандартизований в ISO/IEC 18033-2 [42]. Технічні вимоги до механізму описані в [42].

Для реалізації механізму виконуються такі алгоритми:

• генерація асиметричної ключової пари;

• інкапсуляція ключової пари;

• де інкапсуляція ключової пари.

Генерація асиметричної ключової пари та формування вихідних даних. ECIES-KEM механізм , як і ECIES, реалізований на еліптичній кривій. Це означає, що спочатку необхідно отримати справжні загальні параметри(див. 13.6) , в тому числі базова точка Р порядку p = n. В цьому випадку значення p дорівнює параметру захисту l.

Генерація асиметричної ключової пари та формування вихідних даних виконуються в такій послідовності.

1). Випадковим чином генерується ціле особисте( таємне) число - ключ s із інтервалу ( 1, 2, …, n-1) , тобто

. 1n-1 (13.89)

2). Обчислюється відкритий ключ у вигляді точки еліптичної кривої

W = s Р (13.90).

3). Формується відкритий кортеж p_k та конфіденційний s_k

й . (13.91)

4). Виводиться асиметрична пара ключів та параметрів

(13.92).

Алгоритм інкапсуляції ключа. Алгоритм інкапсуляції є імовірнісним алгоритмом, вхідними даними для якого є відкритий ключ p_k. Для застосування алгоритму повинна бути узгоджена функція вироблення ключів KDF(×).

Алгоритм інкапсуляції виконується у такій послідовності( але при невідомому ключі s_k).

1). Генерується випадкове ціле число – ключ сеансу

. (13.93)

2). Обчислюється відкритий ключ сеансу у вигляді точки еліптичної кривої

С:= r P (13.94)

3). Обчислюється точка еліптичної кривої

. (13.95)

4). Перевіряється, що

Q O

5). Вибирається х – координата точки

. (13.96)

6). Обчислюється значення таємного ключа K:= KDF(C II x).

7). Виводиться інкапсульована асиметрична пара ключів (К, С).

Алгоритм де інкапсуляції ключа. Вхідними даними для алгоритму де інкапсуляції є відкритий ключ C, що генерований при інкапсуляції, та секретний ключ s_k, який також генерований при інкапсуляції. Для застосування алгоритму повинна бути узгоджена функція вироблення ключів KDF(×).

Алгоритм де інкапсуляції виконується у такій послідовності.

1). Обчислюється точка

Q: =s C. (13.97)

2). Перевірити що Q 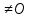. Якщо дорівнює, то вивести Invalid Ciphertext і зупинити виконання алгоритму.

3). Виділити х - координату точки Q .

4). Обчислити та встановити таємний ключ

K:= KDF(C II x). (13.98)

.5). Вивести таємний ключ K.

Відносно безпечності механізму необхідно відзначити таке. Як слідує із [ 6, 37] єдиними атаками для котрих ECIES-KEM уразливий, є атака з використанням побічного каналу, атака «промаху» [37] й силова атака, заснована на використанні груп еліптичної кривої [6].

Також необхідно відмітити, що Механізм ECIES-KEM є НШ, так як інкапсуляція виконується з використанням відкритого кортежу параметрів, а де інкапсуляція і особистого і відкритого.

Додаток А