16.2Оцінки стійкості мас кодів при імітації та підміні

Аналіз показує,що для підміни повідомлень, порушник має сформувати та відповідний автентифікатор. Це може бути зроблено двома способами: шляхом імітації та підміни.

У випадку імітації порушник робить автентифікацітор , ґрунтуючись на апріорних ймовірностях розподілів МАС значень та ключових даних. Імовірність імітації буде визначатися максимальною імовірністю того, що сформований автентифікаторє істинним:

. (4.25)

При рівно ймовірному виборі ключа, що еквівалентно вибору , необхідно враховувати розподіл МАС значень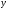для конкретного повідомленняпо ключовому просторі. Для імовірності імітації, що позначимо через імовірність імітації по ключу, справедливим є такий вираз:

, (4.26)

де - кількість геш-функцій, що породжують для повідомленнязначення МАС коду.

Зрозуміло , що

. (4.27)

Крім того, всі записи в стовпцях масиву МАС кодів зустрічаються однакову кількість разів, маємо:

.

Тому верхня границя ймовірності імітації МАС коду по ключу визначається максимальним значенням по всьому просторі повідомлень, а значення імовірності обмежується таким співвідношенням:

. (4.28)

Якщо не враховувати розподіл МАС значень для даного повідомленняпо ключовому просторі, тоді ймовірність імітації позначимо як імовірність імітації по МАС значенню. Імітація через нав'язування МАС значення визначається тим, що з множини передбачуваних МАС кодів вибирається одне. Імовірність успіху буде визначатися виразом:

, (4.29)

де – потужність множини можливих МАС значень для повідомлення.

Якщо МАС значення для повідомлення приймають повну множину значень, одержимо

.

У загальному випадку справедлива така нижня границя:

. (4.30 )

Якщо для повідомлення відомим є статистичний розподіл МАС значень, то оцінка для імовірності імітації по МАС значенню зводиться до оцінки імовірності імітації по ключу.

Верхня границя для імовірності імітації по МАС значенню буде визначається максимальним значенням по всьому простору повідомлень:

. (4.31 )

Атака підміни заснована на тому, що порушник спостерігає та змінює його на, де .Імовірність підміни визначатиметься такою умовною імовірністю:

. (4.32 )

Вираз для імовірності підміни з використанням формули повної імовірності та статистики сприятливих спостережень матиме такий вигляд:

. (4.33 )

Верхня границя імовірності нав'язування шляхом підміни повідомлень та КАП визначається максимальною імовірністю успіху для всіх пар повідомлень, але за умови рівно ймовірного вибору ключа.

Аналіз показує, що можливі два випадки, коли підміна повідомлення на, якщоздійснюється з тим самим автентифікатором,(підміна першого роду) і з різними(підміна другого роду).

Імовірність підміни за умови рівності визначається імовірністю колізії МАС коду та оцінюється виразом:

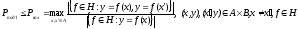.(4.34 )

Для ймовірності підміни другого роду у випадкумаємо:

(4.35)

Таким чином ля точного обчислення імітаційної та колізійної стійкості МАС кодів по наведеним формулах необхідно використовувати статистику спільних розподілів МАС кодів по ключах для істинних та підроблених повідомлень. Для практичних МАС кодів визначення такої статистики виглядає проблематичним через надзвичайно великі розміри масиву можливих МАС Нижні границі для імовірностей імітації та підміни не враховують статистичні властивості масивів автентификаторів, ґрунтуються на моделі псевдовипадковості функції та визначають мінімальні вимоги до розміру ключового простору, та простору МАС значень. Верхні границі для ймовірностей імітації та підміни пов'язані з комбінаторними властивостями МАС масивів та оцінюють значення колізій у просторідля найгіршого випадку вибору ключів та повідомлень.