Практичні заняття № 6

з дисципліни «Прикладна криптологія»

Навчальні питання

Приклади розв’язку задач до 3 розділу асиметричні шифри.

ЗАДАЧА 3.11.1. Побудувати пару (Ek, Dk) для RSA криптоалгоритму, якщо (значення Р і Q у табл. 3.11.1).

Таблиця 3.11.1 – Значення Р і Q

N	1	2	3	4	5	6	7	8	9	10
Pп	29	11	11	11	23	7	29	17	19	19
Qп	11	17	23	13	17	23	7	7	7	11

Розв’язок задачі

Нехай Р=11 і Q=17.

Знаходимо модуль Nта значення функції Ейлера(N):

.

Порівняння виду:

,

запишемо у вигляді Діафантовогорівняння:

.

Вибравши випадково E_k= 37, ключ взаємопростий з функцією Ейлера, тобто (E_k,  (N)) = 1 маємо:

.

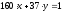Тепер представимо a/b у вигляді ланцюгового дробу:

;

160/37=4+12/37;

37/12=3+1/12;

12/1=12+0.

Таким чином,.

Знаходимо рекурентне значення а₁:

Розраховуємо значення якщо

Підставивши значення а₁, маємо:

Таким чином, пара складає RSA ключову пару.

Перевірка

Підставивши значення ключів E_k =37та D_k = 13 маємо:

.

Задача 3.11.3 Зашифруйте направлено та розшифруйте повідомлення М застосовуючи RSA та використовуючи дані відносно параметрів та ключів, що наведені в таблиці 3.11.3.1. Ключову пару генеруйте знаючи один із ключів, що наведений в останній строчці таблиці 3.18.

Таблиця 3.11.3.1 – Параметри та ключі до задачі 3.11.3.

N	1	2	3	4	5	6	7	8	9	10
Mi	3	4	2	2	3	2	3	2	3	4
Pп	29	11	11	11	23	7	29	17	19	19
Qп	11	17	23	13	17	23	7	7	7	11
Ej /Dj	-/7	-/11	-/3	-/5	-/3	7/-	11/-	13/-	5/-	3/-

Розв’язок.

Розв’яжемо задачу для варіанта № 9: M_i = 3, P_n = 19, Q_n = 7, E_j = 5.

1. Як відомо, у RSA-криптосистемі відкритий і особистий ключі зв’язані наступним співвідношенням:

ED 1 (mod ((N))) (1)

Знайдемо значення N та функції Ойлера від N:

N = PQ = 197 = 133; (N) = (P-1) (Q-1) = 618 = 108.

Необхідно розв’язати рівняння (1) відносно D:

5D 1 (mod 108).

Представимо рівняння у вигляді:108x + 5y = 1.

Розв’яжемо його методом ланцюгових дробів.

Кількість кроків = 3.

y = D_j= = = -.

= = 21;

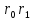= + 1 = 211 + 1 = 22;

= + = 221 + 21 = 43;

= + = 432 + 22 = 112.

y = - 43 mod 108 = 65 D_j = 65.

Зробимо перевірку, підставивши D_j у рівняння (1):

565 1 (mod 108);

325 1 (mod 108);

1 1 (mod 108).

2. Виконаємо направлене зашифрування і розшифрування повідомлення M_i = 3.

ЗАДАЧА 3.11.6. В RSA системі відкритим ключем направленого зашифрування є число E_J=47, а модуль перетворення N = 11303. Знайдіть особистий ключ розшифрування D_J.

Розв’язок

Спочатку нам потрібно факторизувати число N. Використаємо для цього метод квадратичного решета.

Далі знайдемо функцію Ойлера:

Для знаходження потрібно розв’язати рівняння . Розв’язуємо це діафантове рівняння, використовуючи ланцюгові дроби:

Перевіримо результат:

Отже

ЗАДАЧА 3.11.7 Знайдіть середнє число ітерацій розвязку діафантового рівняння при побудові ключової RSA пари (E_k , D_k)( дивись (3.13), ), якщо E_k = =2^{512 + k 256}, k – номер реєстрації.

Діафантове рівняння – це рівняння виду:

,

де – цілочисельні коефіцієнти, – невідомі.

При побудові ключової RSA пари (E_k , D_k) нормоване діафантове рівняння матиме вигляд:

,

де – функція Ейлера, – деяке число, – відкритий ключ, – особистий ключ.

При відкритий ключ .

Формула, для знаходження середнього числа ітерацій розв’язку діафантового рівняння має вигляд:

(ітер).

Задача 3.11.8 Знайдіть відкритий ключ Y асиметричної пари (x, Y) в скінченному полі GF(23) , якщо первісний елемент М=15, а особистий ключ х = 20.

Розв’язок

Спочаткуперевіримо, чи є М=15 первісним елементомGF(23). Для цього він повинензадовільняти вимогам:

1. або ;

2. , де а – один з множників канонічного розкладу числа Р.

Проведеморозрахунки для заданихзначеньР та М:

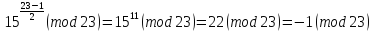- перша умовавиконується. Далізнайдемоканонічнийрозклад числа Р та перевіримо другу умову:

23 - 1 = 22 = 2 ∙ 11- отже, а₁ = 2 і а₂ = 11.

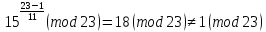
Таким чином умов 2 такожвиконується, а, отже, М – первіснийелемент у поліGF(23)/

Відкритий ключ Yасиметричної пари (x, Y) можна знайти за формулою Y = М^ХmodN. Підставимо задані значення M, x та N:

Y = 15²⁰mod23 = 332525673007965087890625mod 23 = 9

ЗАДАЧА 3.11.11 Зашифруйте та розшифруйте повідомлення М=(13,17), використовуючи направлений шифр в групі точок ЕК, якщо Р=23, a=1, b=1 (крива y²=(x³+x²+1)mod23), G=(17,20), n=7.

Решение:

Отправитель сообщения выбирает случайное (k=3).

Расчитывают одноразовый открытый ключ

C1=k*G=3*(17;20)

λ=(3+a)/2y1(mod 23)=(3*17*17+1)/40(mod 23)=848/40(mod 23)=1

2G=(13;7)

λ=(y2-y1)/(x2-x1)(mod 23)=(7-20)/(13-7)(mod 23)=9

3G=(5;19)

Одноразовый открытый ключ=(5;19)

Q=d*G-открытый ключ получателя

d-долговременный собственный ключ (d=2)

Q=2G=2*(17;20)=(13;7)

C2=M+k*Q=(13;7)+3*(13;7)

2(13;7)=(5;4)

3(13;7)=(17;3)

Получателю посылают открытый ключ и зашифрованный текст

Расшифрование :

Получатель вычисляет d*= 2(5;19)

- d*= (11;22)- (17; 3)= (11;22)+(17;-3)=(11;22) + (17;20)

_{ЗАДАЧА 3.11.12.}

Сформуйте пропозиції та реалізуйте алгоритм направленого шифрування в групі точок еліптичних кривих, якщо порівняння кривої має вигляд:

y²=(x³+x+6)mod11, G=(2,7),

особистий ключ х_i=7.

Знайдіть відкритий ключ А_i користувача. Виробіть криптограму С_М , якщо М=(10,9), k=3. Сформуйте пропозиції та здійсніть розшифрування криптограми С_М.

_{Розв’язок задачі}

_{Направлене шифрування повідомлення М буде здійснюватися наступним чином:}

_{С2 = M + kQ}

_{де k — сеансовий ключ (обирається випадково при початку нового сеансу)}

_{Q — відкритий ключ користувача А, котрому адресується повідомлення.}

_{Також обчислюється відкритий ключ сеансу:}

_{С1 = kG}

_{де G — базова точка.}

_{Таким чином криптограма складається з двох точок на еліптичній кривій: (С1, С2).}

_{Розшифрування відбувається наступним чином:}

_{Користувач А, котрому була адресована криптограма впевнюється, що пара точок (С1, С2) належать еліптичній кривій. Далі отримується початкове повідомлення як:}

_{M’ = C2 - dC1 = M + kQ - dkG = M + kdG - dkG = M}

_{Таким чином криптоперетворення є зворотнім та однозначним.}

_{Тепер нехай рівняння кривої має вигляд y2 = x3+x+6, а базова точка G=(2,7).}

_{Здійснимо шифрування повідомлення М = (10,9) згідно алгоритму, наведеного вище, використовуючи ключ сеансу k=3. Розрахуємо відкритий ключ абонента:}

_{Q = dG = 7(2, 7) = (7, 2)}

_{Далі зашифруємо повідомлення:}

_{C2 = M+kQ = (10, 9) + 3(7, 2) = (10, 9) + (3, 5) = (10, 2)}

_{А також відкритий ключ сеансу:}

_{C1 = kG = 3(2, 7) = (8, 3)}

_{Таким чином, зашифроване повідомлення представляє собою пару точок (С1, С2) = ((8, 3), (2, 7)).}

_{Тепер розшифруємо повідомлення:}

_{M’ = C2 - dC1 = (10, 2) - 7(8, 3) = (10, 2) - (3, 5) = (10, 9)}

_{Як видно, М та М’ співпадають, отже розшифрування відбулося вірно.}

ЗАДАЧА 3.11.12. Обґрунтуйте пропозиції та реалізуйте алгоритм направленого шифрування в групі точок еліптичних кривих, якщо рівняння кривої має вигляд:

y²=(x³+x+6)mod11, G=(2,7), особистий ключ ni=7. Знайдіть відкритий ключ Аi користувача.

Виробіть криптограму С(М) , якщо М=(10,9), k=3. Зробіть пропозиції та здійсніть розшифрування криптограми С(М).