14.4 Методи автентифікації в класі симетричних шифрів

Всі методи автентифікації можна розділити на 2 класи: ті, що реалізуються збитковістю, і ті, які без збитковості [12, 13, 54, 61, 94, 95, 142, 273].

Твердження 4.1

Поточне шифрування є необхідною, але не достатньою умовою забезпечення цілісності та справжності переданої інформації.

Доведення. Розглянемо поточне двійкове шифрування. Нехай є повідомлення.– функція зашифрування

, (4.15 )

де – початковийj-й ключ. Тоді

. (4.16 )

Покладемо, що КРА може перехопити тільки та зможе сформувати послідовність(яку-небудь). Тоді він формує. Вважатимемо, що ЗЗІ має синхронізацію по і. Тоді при відновленні повідомлення отримаємо: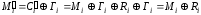. Таким чином, можна нав'язати хибне повідомлення. Твердження доведено.

У більшості додатків джерело не довіряє. Більш того, обоє прагнуть захисту засобом арбітражу. Це може бути досягнуто, якщо в системі використовується асиметрична криптографія.

Твердження 4.2

Використання потокового шифрування та групових кодів, що знаходять та виправляють помилки, є необхідною, але не достатньою умовою забезпечення цілісності та справжності інформації, що захищається.

Доведення. Нехай М – інформація. – блоки інформаціїМ. При груповому кодуванні обчислюються контрольні символи як

. (4.17)

Після цього в систематичному груповому коді кожному блокові додається КС: . На приймальній стороні в декодері на основі КС знаходяться та виправляються помилки, якщо їх не більше, ніж виправна здібність коду. Для захисту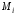використовується поточне шифрування:

. (4.18 )

Групові коди володіють властивістю, що операція є дозволеною комбінацією цього ж коду, тобто властивість замкнутості:

.

Якщо КРА може нав'язати хибну інформацію методом модифікації, до-давши 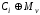, то декодер приймеі цієї модифікації не виявить.

Твердження доведено.

Висновок: відповідно до Твердження 4.2 у поточних системах, які використовують групові коди, може нав'язуватися інформація як випадкового так і визначеного змісту.

Твердження 4.3

Необхідною і достатньою умовою забезпечення цілісності та справжності в системах потокового шифрування є:

• використання потокового шифрування;

• використання групових кодів, що виявляють помилку;

• формування гами шифрування з використанням раніше переданих символів криптограми або відкритої інформації.

Роздивимося рис. 4.2 та 4.3

Рисунок 4.2 – Алгоритм формування гами зашифрування

Рисунок 4.3 – Алгоритм формування гами розшифрування

, (4.19 )

де . (4.20 )

У нашому випадку зашифрування

, (4.21)

а розшифрування

(4.22 )

Якщо , тобто її сформувано правильно, то. І вирази з сумами відповідно дорівнюють 0. При інформацію прийнято пра-вильно.

Якщо , то- повідомлення розшифровано з помилками.