14.3 Вступ у теорію автентичності Сімонсона

У 70-і роки вперше була опублікована теорія захисту від обману (автентичності), що отримала найменування теорії Сімонсона [142, 12, 13, 273].

Сутність теорії Сімонсона:

У теорії Сімонсона покладається, що два користувачі івзаємодіють між собою по відкритій телекомунікаційній системі (ТС) і для обміну між ними виділяється одноразовий ключ автентифікації.

Вважатимемо, що простір повідомлень може бути сформований зповідомлень.

Захист інформації здійснюється в ЗЗІ (рис. 1.4).

В ЗЗІ формується криптограма

. (4.2 )

В подальшому - передається по ТС, а потім ЗЗІ відновлює інформацію:

. (4.3 )

Вважатимемо, що джерело криптограм формує 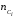– криптограм. Якщо КРА сформує безліч криптограмі одну з них передав, то він може обманути з імовірністю [13, 142. 273]

(4.4 )

де – імовірність обману.

Якщо , то імовірність нав'язування повідомлення, тобто обману, дорівнює 1.

Наша задача – зменшити , для цього необхідно збільшити простір криптограм:

або . (4.5)

Для створення безумовно стійкої системи , тоді час передачі інфор- мації буде t. Зі сказаного випливає, що ніколи не можна реалізувати криптографічний захист, коли , можна тільки як найбільше зменшити.

В теорії Сімонсона прийнято визначати імовірність обману, використовуючи (4.4 ).

Якщо =, то в системі може бути нав'язане повідомлення випадкового змісту. Так КРА в моделі рис.4.1 може реалізувати такі загрози:

• імітація, P_i- ймовірність імітації;

• підміна, P_n- ймовірність підміни;

• передача раніше переданого повідомлення з імовірністю P_рп;

• - ймовірність всіх останніх загроз.

При проектуванні та оцінці автентичності необхідно визначити, яка загроза є найбільш небезпечною.

У своїй теорії Сімонсон здійснює оцінку за однією найбільш небезпечною загрозою

. ( 4.6 )

Він визначив як максимальну загрозу із всієї множини загроз.

Покладемо, що джерело разом з ЗЗІ формують криптограмута відомий апріорний ряддля. При відомомуможна знайти ентропію джерела криптограм:

. (4.7 )

КРА, перехоплюючи криптограми, намагається визначити ключ автентифікації, який використовується для забезпечення цілісності та справжності (достовірності). Незнання КРА відносно ключа або надмірності, внесеної в криптограму, можна записати як умовну ентропію, що ключ використовується для криптограми:

(4.8 )

причому – вважаємо відомою.

Визначимо, яку кількість інформації 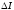отримав КРА при переході віддо:

.

Сімонсон показав, що для моделі (4.6), коли вибирається тільки одна загроза, ймовірність обдурювання може бути обчислена за формулою:

. (4.9 )

Знайдемо із (4.9) :

. (4.10 )

Вираз (4.10) у теорії Сімонсона визначає межу ймовірностей обману в системі.

Розглянемо (4.10).

1. Криптосистеми, у яких досягається рівність (4.10), називаються системами з найкращим способом автентичності (повністю автентичні).

2. Для зменшення ймовірності обману необхідно збільшувати , тобто кількість інформації, що міститься в криптограмі про ключ автентифікації.

3. Для забезпечення цілісності та достовірності необхідно вводити до-датковий ключ автентифікації . Таким чином у нашій системі з'являється 2 ключі – ключ шифруваннята ключ автентифікації.

4. Імовірність обману

, (4.11 )

де – довжина імітоприкладки (коду автентифікації).

Розглянемо (4.4) та (4.11). Нехай довжина повідомлення буде бітів. Довжина контрольної суми. Тоді довжина криптограми:

. (4.12 )

Для двійкового алфавіту

. (4.13 )

Підставимо (4.13) у (4.4 ):

. (4.14)

Тобто (4.14) співпадає з (4.11).